《固体物理学》课程授课教案(讲义)第四章 晶格振动

第四章晶格振动 S4.1简谐振动和简正坐标 一、简谐近似 一般地,晶格的势能可写为格点位置坐标的函数, V=VRn+u,0}(3.1- 其中, Rn=n,+n,a2+n,=na,(3.1-2) 是第n个格点的平衡位置,u{是1时刻第n个格点相对R的偏离。 y可以展为泰物级数(在平衡位置R处展开): (\=0(平衡位置) u.) 并令'(R)=0为零势点参考点,当略去2阶以上高阶项时, 2 (3.1-) 此式即为简谐近似下品格的势能表达式。换句话说,仅保留品格势能函数的展开式的2阶项 的近似称为简谐近似。 品格的动能为各格点的动能之和, T芝m或61-2》 2、简正坐标 为简化晶格的动能和势能的表达式(消去交叉项),由分析力学知可引入简正坐标Q。 即作如下正交变换, i,(=Vm,4)=a2,(31-3) 1
1 第四章 晶格振动 §4.1 简谐振动和简正坐标 一、简谐近似 一般地,晶格的势能可写为格点位置坐标的函数, V VR u (t) (3.1 ~ 1) n n 其中, (3.1 2) n i i R n a n a n a n a 1 1 2 2 3 3 是第 n 个格点的平衡位置,un{t}是 t 时刻第 n 个格点相对 Rn 的偏离。 V 可以展为泰勒级数(在平衡位置 Rn 处展开): N i N j i j i j N i i i n N n m n m n m N n n n u u u u V u u V V V V V V 3 1 3 1 0 3 2 1 0 0 1 , 0 2 1 ( ) : 2 1 ( ) R R u u u 0 0 ui V (平衡位置) 并令 ( ) 0 V0 Rn 为零势点参考点,当略去 2 阶以上高阶项时, (3.1 1) 2 1 3 1 3 1 0 2 N i N j i j i j u u u u V V 此式即为简谐近似下晶格的势能表达式。换句话说,仅保留晶格势能函数的展开式的 2 阶项 的近似称为简谐近似。 晶格的动能为各格点的动能之和, (3.1 2) 2 1 3 2 N i T miui 2、简正坐标 为简化晶格的动能和势能的表达式(消去交叉项),由分析力学知可引入简正坐标 Qj。 即作如下正交变换, ( ) (3.1 3) ~ui miui aijQj

注:利用了爱因思坦求和规则,即两个相同指标表示求和。 (3.1一3)式的逆变换是, Q,=a(3.1-4) 变换系数a,满足正交条件 (1 j=k da=a-0 (3.2-5) 利用31-3)式,(31-)和31-2)试可化为如下正定形式, r-2g6i-0 -2 (3.1-7) 3、体系的哈密顿量 由分析力学知,多粒子体系的拉格朗日函数, L=T-V, 正测动量月=影=0 (3.1-8) 哈密顿量 H=T+r-2g+0)-24,6I-) 说明在简谐近似下,利用简正坐标,晶格的振动化为3N个独立的谐振子。 4、振动模 2,-0m 应用正则方程{ (3.1-10) g 31-8C== aH 80, 可得Q+og=0(3.1-11) (l,2,3,3N
2 注:利用了爱因思坦求和规则,即两个相同指标表示求和。 (3.1-3)式的逆变换是, (3.1 4) ~ Qj aijui 变换系数 aij满足正交条件, * 1 (3.2 5) 0 ij ik jk j k a a j k 利用(3.1-3)式,(3.1-1) 和(3.1-2)式可化为如下正定形式, (3.1 6) 2 1 3 1 2 2 N i V i Qi (3.1 7) 2 1 3 1 2 N i T Qi 3、体系的哈密顿量 由分析力学知,多粒子体系的拉格朗日函数, L T-V , 正则动量 (3.1 8) i i i Q Q L P 哈密顿量 ( ) (3.1 9) 2 1 3 1 3 1 2 2 2 N i i N i H T V Pi iQi H 说明在简谐近似下,利用简正坐标,晶格的振动化为 3N 个独立的谐振子。 4、振动模 应用正则方程 (3.110) i i i i Q H P P H Q 可得 0 (3.1 11) 2 Qi i Qi (i=1,2,3,., 3N) 由(3.1-8), , i i i Q H Q P

这是一个关于简正坐标Q,的独立的谐振方程,表明了简正坐标的意义,即简正坐标描述晶 格中独立的简谐振动,这种独立的振动共有3N个。这样在简正坐标下,具有3N个自由度 的晶格的振动被简化为3N个独立简谐振动(即3N个独立的弹簧)。 (3.1-11)式的解为2,=A,sin(o1+8)(3.1-12) 由和Q,的正交变换关系(3.1-3)知,当仅考虑一种简正振动2时, 1 m4@1+8)B1-13) 这里,1-1,2,3,3N· 所以, (1)一个简正振动并不代表一个格点的振动,而是代表所有格点的同频集体振动,称为 一个振动模式(简称一个振动模)。 (2)晶格中格点(原子)的真实振动是所有3N个简正振动(振动模)的叠加。 至此我们已看到: 所谓“简谐近似“即简化为谐振的近似: 所谓“简正坐标”即使系统的势能和动能都简化为正定形式的坐标。 5、振动模的能量和本征态 品格振动必须用量子力学来处理。 作特代P→防品 (3.1-9)式可化为量子力学形式 o+o0)-2u (3.1-8) (3.1-8)为3N个独立谐振子的哈密顿之和。对每一谐振子有薛定谔方程 +名+gmg=tQ)a1-司 其解为熟知的, 8=(+h@, (本征能量) 3
3 这是一个关于简正坐标 Qi 的独立的谐振方程,表明了简正坐标的意义,即简正坐标描述晶 格中独立的简谐振动,这种独立的振动共有 3N 个。这样在简正坐标下,具有 3N 个自由度 的晶格的振动被简化为 3N 个独立简谐振动〔即 3N 个独立的弹簧〕。 (3.1-11)式的解为 Q A sin(t ) (3.112) i i i 由 ui和 Qi的正交变换关系(3.1-3)知,当仅考虑一种简正振动Qk 时, sin( ) (3.1 13) 1 1 1 1 3 1 a A t m a Q m a Q m a Q m u ik k k i ik k i N j ij j i ij j i i 这里,i=1,2,3,., 3N 。 所以, (1)一个简正振动并不代表一个格点的振动,而是代表所有格点的同频集体振动,称为 一个振动模式(简称一个振动模)。 (2)晶格中格点(原子)的真实振动是所有 3N 个简正振动(振动模)的叠加。 至此我们已看到: 所谓“简谐近似”即简化为谐振的近似; 所谓“简正坐标”即使系统的势能和动能都简化为正定形式的坐标。 5、振动模的能量和本征态 晶格振动必须用量子力学来处理。 作替代 i i Q P i (3.1-9)式可化为量子力学形式, ( ) (3.1 8) 2 1 3 1 3 1 2 2 2 2 2 N i i N i i i i Q H Q H (3.1-8)为 3N 个独立谐振子的哈密顿之和。对每一谐振子有薛定谔方程, ( ) ( ) ( ) (3.1 8) 2 1 2 2 2 2 2 i i i i i i Q Q Q Q 其解为熟知的, i i i n ) 2 1 ( (本征能量〕

,@-层eg-以,)(体 -贤e 系统的总能量和总本征态为 E-Z Ψ=im,g) 4
4 ) ( ) 2 ( ) exp( n i i i n i i i Q H (本征态) i i i Q 系统的总能量和总本征态为 N i E i 3 1 N i n Qi i 3 1 ( )

4.2一维单原子链 一、振动方程及格波解 1、振动方程 设链上原子间的相互作用仅存在于 最近邻原子之间,并且近邻原子间的相产2一月2 互作用势能为 Vn(a+δn),则体系的总势能为, 10 900 u-2a+6) (3.2-1) —维单原子链 δ。为第n个原子相对于平衡位置的 偏离。 简谐近似下, u2器袋0 相邻原了间的作用力,了=一 第n个原子的受力为,f+f云 ∫&=-B(ua-m.) f=-B(u,-山+》 所以,第n个原子的牛顿运动方程为 mim=f+f右=(4*+4r1一2)(3.2-4) 这里,n=l,2,3,N。 即:对N原子链,共有N个这样的联立方程(齐次线性方程)。 2、格波解 可以验证(32一4)式具有下列形式的解, u,(q)=un=Aee-g)(3.2-5) 将(3.2-5)式代入(32-4)可得:
5 4.2 一维单原子链 一、振动方程及格波解 1、振动方程 设链上原子间的相互作用仅存在于 最近邻原子之间,并且近邻原子间的相 互作用势能为 vn a n ( ),则体系的总势能为, ( ) (3.2 1) 1 N n n a n U v n 为第n个原子相对于平衡位置的 偏离。 简谐近似下, (3.2 2) 2 1 2 1 1 2 0 2 2 1 2 0 2 2 N i n n N i n n U v U 相邻原子间的作用力, (3.2 3) 2 2 n n n a n n U v f 其中, n a n v 2 2 为近邻原子间的弹性系数。 第 n 个原子的受力为,f=f 左+f 右 f 左=-(un-un-1) f 右=-(un-un+1) 所以,第 n 个原子的牛顿运动方程为 mun f 左+f 右=( un+1+ un-1-2 un) (3.2-4) 这里,n=1,2,3,.,N。 即:对 N 原子链,共有 N 个这样的联立方程(齐次线性方程)。 2、格波解 可以验证(3.2-4)式具有下列形式的解, ( ) (3.2 5) ( ) i tnaq un q unq Ae 将(3.2-5)式代入(3.2-4)可得:

02=291-c0sag(32-6) (3.2-6) m 即:只要o与q满足关系(32-6),(3.2-5)式就是联立方程(32-4)的解。 (3.2-5)式中A为振幅,o为角频率,0g为第n个原子的振动位相因子。(注:振幅 A和角频率o是格波的函数,即A=A()=A:o=o(g)=ag·所以:q格波引起的第n个原 子的位移(振动方程3.2-5)式)为, ,(g)==Ae"- 而原子的实际总位移是所有格波的叠加, un=∑4.(q)=∑A,e 问题*:证明一维单原子晶格的简正坐标可以写为 0g=4”,线胜线线系数动,产次。 (42一5)为平面波形式,表明在简谐近似下,晶格中原子的振动是以平面波的形式存在的, 这种波称为格波(相对于连续波)。 二、布里渊区和周期性边条件 1、布里渊区 若将(3.2-5)中的a叫换成ag+2m(m为整数),则格波解(32-5)不变。这表明可 将g限定在一定的取值范围,在此范围之外不存在新的格波解,为此取 -x<aqsn 或-a<gsla(3.2-7) 由(32-7)定义的q的取值范围,包括了所有可解的格波解,称为布里渊区。 2、有限介质玻恩一卡曼条件(周期性边条件) 对于有限链情况,两端的原子只受到一个近邻原子的作用,联立方程的形式(在端点) 发生变化,求解就复杂了,为此常利用玻恩一卡曼条件:将N个原子有限链看作头尾相接 的环。这时,方程(32-4)及其解仍然适用,只是要求N+1号原子就是1号原子: Ung =UNl 也即:
6 (1 cos ) (3.2 6) 2 2 aq m 或 ) (3.2 6) 2 1 sin ( 2 4 2 aq m 即:只要与 q 满足关系(3.2-6),(3.2-5)式就是联立方程(3.2-4)的解。 (3.2-5)式中 A 为振幅,为角频率,naq 为第 n 个原子的振动位相因子。(注:振幅 A 和角频率是格波的函数,即 A=A(q)=Aq;=(q)=q。所以:q 格波引起的第 n 个原 子的位移(振动方程(3.2-5)式)为, ( ) ( ) i t naq n nq q q u q u A e 。 而原子的实际总位移是所有格波的叠加, q i t naq q q n n q u q A e ( ) u ( ) 问题**:证明一维单原子晶格的简正坐标可以写为 i t q q Q q NmA e ( ) ; 线性变换系数为 inaq nq e N a 1 (4.2-5)为平面波形式,表明在简谐近似下,晶格中原子的振动是以平面波的形式存在的, 这种波称为格波(相对于连续波)。 二、布里渊区和周期性边条件 1、布里渊区 若将(3.2-5)中的 aq 换成 aq+2m (m 为整数),则格波解(3.2-5)不变。这表明可 将 aq 限定在一定的取值范围,在此范围之外不存在新的格波解,为此取 -<aq 或 -/a<q/a (3.2-7) 由(3.2-7)定义的 q 的取值范围,包括了所有可解的格波解,称为布里渊区。 2、有限介质 玻恩-卡曼条件(周期性边条件) 对于有限链情况,两端的原子只受到一个近邻原子的作用,联立方程的形式(在端点) 发生变化,求解就复杂了,为此常利用玻恩-卡曼条件:将 N 个原子有限链看作头尾相接 的环。这时,方程(3.2-4)及其解仍然适用,只是要求 N+1 号原子就是 1 号原子: u1q u(N 1)q 也即:
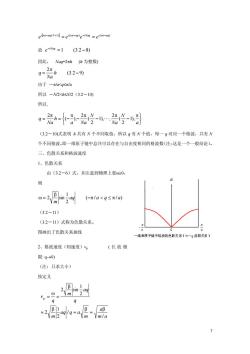
ef-ag(=el(e-ag)e-Nag =ef(e-ag) 故e-=1(32-8) 因此,NagF2xh(h为整数) 9-0462-9 由于-la<gsla 所以-N2<hsN2(32-10) 所以, g急-急-老兮- (32-10)式表明h共有N个不同取值,所以g有N个值,每一q对应一个格波,共有N 个不同格波。即一维原子链中总共可以存在与自由度相同的格波数(注:这是一个一般结论)。 三、色散关系和格波速度 1、色散关系 由(32-6)式,并注意到物理上要20, (-π/a<q≤π/a) (32-11) (32-11)式称为色散关系。 图画出了色散关系曲线 维单原子链中格波的色散关系(0~?函数关系) 2、格波速度(相速度)V。 (长波极 限:q→0) (注:只求大小) 按定义 2g悟- 7
7 i t aq(N 1) i( t aq) iNaq i( t aq) e e e e 故 1 (3.2 8) iNaq e 因此, Naq=2h (h 为整数) (3.2 9) 2 h Na q 由于 -/a<q/a 所以 -N/2<hN/2(3.2-10) 所以, a N Na N a Na h Na q 1), 2 ( 2 1), , 2 ( 2 ( ), 2 (3.2-10)式表明 h 共有 N 个不同取值,所以 q 有 N 个值,每一 q 对应一个格波,共有 N 个不同格波。即一维原子链中总共可以存在与自由度相同的格波数(注:这是一个一般结论)。 三、色散关系和格波速度 1、色散关系 由(3.2-6)式,并注意到物理上要0, 则 ( / / ) 2 1 2 sin aq a q a m (3.2-11) (3.2-11)式称为色散关系。 图画出了色散关系曲线 2、格波速度(相速度)vp ( 长 波 极 限: q0) (注:只求大小) 按定义 m a a m aq q a m q aq m q v p / / 2 1 2 2 1 2 sin

注意到F=-B8=-Ba 则pa为伸长模量(y) 所以,=(白2(m线密度 这表明,在长波极限(q0),品格中传播的格波就象在连续介质中传播一样,这也是从微观 角度对连续介质的波速公式的论证。(习题) 3、群速度 (能量传播的速度,波包的速度) (注:只求大小) 按定义可求出。 dg 显然,q=士π/a=0。即,布里渊区边界处,群速度为零。其实,q=士π/a对应的 是驻波(~2=2江=2红=2a),所以群速度,=0。 gπ/a
8 注意到 a F a 则为伸长模量() 所以 1/ 2 ( ) vp (=m/a=线密度) 这表明,在长波极限(q~0),晶格中传播的格波就象在连续介质中传播一样,这也是从微观 角度对连续介质的波速公式的论证。(习题) 3、群速度 vg (能量传播的速度,波包的速度) (注:只求大小) 按定义 dq d vg 可求出, ) 2 1 . cos( aq m a dq d vg 显然,q / a, vg 0。即,布里渊区边界处,群速度为零。其实,q / a 对应的 是驻波( a q a 2 / 2 2 ), 所以群速度 vg=0

§4.3一维双原子链(一维复式晶格)、声学波和光学波 一、振动方程及格波解 1、振动方程 ←一个晶胞》 8 ● (2m-2)(2m -13 (2+1)(2m+2) 维双原子链模型 仿照一维单原子链情况,一维双原子链上原子的振动方程为, ml2n=B(31+gm-1-2n)(3.3-1) M1l2m+1=B(en+2+n-2W+)(3.3-2) 这两个方程分别是第个晶胞内两个原子的振动方程。对包含N个原胞的一维双原子 链,共有N个这样的联立方程组(即2N个方程). 2、格波解和色散关系 (3.3-1&2)式具有下列形式的解, “zn(q))=Aew-2nagl zni(q)=Bew-2m+lagl (3.3-3) 注:n是原胞编号。 (3.3-3)代入(3.3-1&2)可得: (mo2-2B)A+(2Bcosaq)B=0] (3.3-4) (2Bcosaq)A+(M@2-2B)B=0] (3.3一4)有解的条件是它的系数行列式为零,即: K(mo2-2B) (3.3-5) (2B cosaq) (Mo-28) 由(3.3一5)式可得, oi=pm+M (3.3-6 mM [将(3.3-6)式带回到(33-4)式可得
9 §4.3 一维双原子链(一维复式晶格)、声学波和光学波 一、振动方程及格波解 1、振动方程 仿照一维单原子链情况,一维双原子链上原子的振动方程为, mu n 2 ( u2n+1+ u2n-1-2 u2n) (3.3-1) Mu n 2 1 ( u2n+2+ u2n-2 u2n+1) (3.3-2) 这两个方程分别是第 n 个晶胞内两个原子的振动方程。对包含 N 个原胞的一维双原子 链,共有 N 个这样的联立方程组(即 2N 个方程)。 2、格波解和色散关系 (3.3-1&2)式具有下列形式的解, (3.3 3) ( ) ( ) [ (2 1) ] 2 1 ( 2 ) 2 i t n aq n i t naq n u q Be u q Ae 注:n 是原胞编号。 (3.3-3)代入(3.3-1&2)可得: (3.3 4) (2 cos ) ( 2 ) 0 ( 2 ) (2 cos ) 0 2 2 aq A M B m A aq B (3.3-4)有解的条件是它的系数行列式为零,即: 0 (3.3 5) (2 cos ) ( 2 ) ( 2 ) (2 cos ) 2 2 aq M m aq 由(3.3-5)式可得, sin ( ) (3.3 6) ( ) 4 1 1 2 1 2 2 2 aq m m mM mM m M [将(3.3-6)式 带回到] 由(3.3-4)式可得

).-2 A 2Bcosag (3.3-7 (33一6)式表明存在两种色散关系:(q)和@.(q,且>@.(如图示)。后面将说明,相 应的格波称为光学波:@相应的格波称为声学波。 二、布里渊区和周期性边 条件 l、布里渊区(Brillouin ,(q) Zone) 若将(3.3-3)中的 2ag换成2ag叶2m(m为 o.(q) 整数),格波解(33一3) 不变。这表明可将2ag π 限定在一定的取值范围, 0 2a 2a 在此范用之外不存在新 两种格波的色散关系:®0-光学波:®.(心-声学波 的格波解,为此取 -π<2agsr 或-元2a<qs元2a(3.3-8) 由(3.3-8)定义的9的取值范围,包括了所有可解的格波解,称为布里渊区。 注意,在布里渊区内,一个g对应两个格波(@(q)和o(q)。 2、周期性边条件 对于有限链情况,两端的原子只受到一个近邻原子的作用,联立方程的形式(在端点》 发生变化,求解就复杂了。为此常利用玻恩一卡曼条件:将2W个原子有限链看作头尾相接 的环。这时,方程(32-1,2)及其解仍然适用,只是要求2N+1号原子就是1号原子: ig uN+1)g 也即: elo1-2ag(N+I]=ei(ot-2aq)e-iN2ag=ei@t-2ag) 6
10 (3.3 7) 2 cos 2 2 cos 2 2 2 aq M A B aq M A B (3.3-6)式表明存在两种色散关系:+(q)和-(q),且+>-(如图示)。后面将说明,+相 应的格波称为光学波;-相应的格波称为声学波。 二、布里渊区和周期性边 条件 1 、 布 里 渊 区 (Brillouin Zone) 若将(3.3-3)中的 2aq 换成 2aq+2m (m 为 整数),格波解(3.3-3) 不变。这表明可将 2aq 限定在一定的取值范围, 在此范围之外不存在新 的格波解,为此取 -<2aq 或 -/2a<q/2a (3.3-8) 由(3.3-8)定义的 q 的取值范围,包括了所有可解的格波解,称为布里渊区。 注意,在布里渊区内,一个 q 对应两个格波(+(q)和-(q))。 2、周期性边条件 对于有限链情况,两端的原子只受到一个近邻原子的作用,联立方程的形式(在端点) 发生变化,求解就复杂了。为此常利用玻恩-卡曼条件:将 2N 个原子有限链看作头尾相接 的环。这时,方程(3.2-1,2)及其解仍然适用,只是要求 2N+1 号原子就是 1 号原子: u1q u(N 1)q 也即: e e e e i t aq N i t aq iN aq i t aq 2 ( 1) ( 2 ) 2 ( 2 )
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《固体物理学》课程授课教案(讲义)第二章 晶体结构的测定.pdf
- 《固体物理学》课程授课教案(讲义)晶体能带结构理解电导特性.doc
- 《固体物理学》课程授课教案(讲义)第六章 固体电子论基础.pdf
- 《固体物理学》课程授课教案(讲义)紧束缚近似理论研究性教学教案设计.doc
- 《固体物理学》课程授课教案(讲义)非谐效应——热膨胀研究性教学教案设计.doc
- 《固体物理学》课程教学大纲 Solid State Physics.pdf
- 《半导体工艺原理》课程教学课件(PPT讲稿)第4章 晶圆制造与外延硅生长.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第2章 集成电路工艺介绍.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第10章 化学气相沉积与电介质薄膜.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第5章 加热工艺.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第1章 半导体制程技术导论.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第2章 集成电路工艺介绍.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第3章 半导体基础原理、组件与制程.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第6章 光刻工艺.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第7章 等离子体的基础原理.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第8章 离子注入.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第9章 蚀刻.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)第11章 金属化工艺.ppt
- 《半导体工艺原理》课程教学课件(PPT讲稿)课程总结回顾(半导体制造技术导论).ppt
- 《理论力学》课程教学资源(PPT课件)机械振动基础.ppt
- 《固体物理学》课程授课教案(讲义)第三章 晶体的结合.pdf
- 《固体物理学》课程授课教案(讲义)第一章 晶体结构.pdf
- 《固体物理学》课程授课教案(讲义)第五章 能带理论.pdf
- 《固体物理学》课程教学资源(参考资料)词汇汉英对照.pdf
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.7 Lattice Sites in a Cubic Unit Cell 1.8 crystal plane and miller index.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.6 typical crystal structure.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.1 Elementary Crystallography 1.2 Crystal Structure ≡ Lattice + Basis 1.3 Lattice Translation Vectors 1.4 Non-Bravais Lattices 1.5 Wigner-Seitz Method.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Introduction.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure(Supplement - microstructure and crystal system).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.9 Elements of Symmetry 1.10 Space groups 1.11 7 crystal system and 14 Bravis Lattice.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice(supplement - Review & Overview of X-Rays).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice 2.6 X-Ray Diffraction Methods 2.7 Applications of XRD.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice(2.1-2.5).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3.3 The cohesive energy for ionic crystal.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3(Supplement - Rules of crystal binding).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3.1 General crystal binding 3.2 typical binding.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.1 Normal Modes of Vibration 4.2 Density of States 4.3 Harmonic approximation and normal mode coordinates 4.4 phonon.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.5 Heat capacity of the lattice.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.1 general background and approximations 5.2 Bloch’s Theorem.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.6 Anharmonic Effects 4.7 Equation of states for Lattice 4.8 Experimental methods for the determinations of lattice vibration spectroscopy.ppt
