《理论力学》课程教学资源（PPT课件）虚位移原理

问题的提出 问题图示平面机构，受水平力P和铅垂力Q作用， 对应任意角度欲使机构保持平衡，P和Q应满足 的比例关系。（忽略各构件自重及摩擦） 0 水利用畅体系统平衡求解需要取多次研究对 象，求解过程烦琐

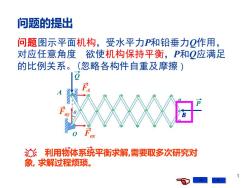
 1 问题的提出 问题图示平面机构，受水平力P和铅垂力Q作用， 对应任意角度 欲使机构保持平衡，P和Q应满足 的比例关系。(忽略各构件自重及摩擦） Fox Foy FA  a a A B O Q P  利用物体系统平衡求解,需要取多次研究对 象, 求解过程烦琐

问题的提出 能否借助动力学的分析方法来求解静力学问题呢？ 平衡条件： Fa-Fb=0 (a) b 在平衡位置附近，AB 杆转动微小角度 杠杆的平衡条件可以用作 用力在平衡附近的微小位 s atgo 移中所作的功来建立 s,=bige 由于在新的位置系统仍然平衡 (b) ???????

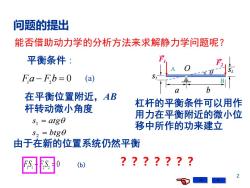
 2 问题的提出   s btg s atg = = 2 1 能否借助动力学的分析方法来求解静力学问题呢？ 平衡条件： F1 a − F2 b = 0 (a)  S1 S2 在平衡位置附近，AB 杆转动微小角度 F1 F2 O a b Ａ Ｂ 由于在新的位置系统仍然平衡 0 1 1 2 2 FS − F S = ？？？？？？？ 杠杆的平衡条件可以用作 用力在平衡附近的微小位 移中所作的功来建立 (b)

第十四章 虚位移原理 1★大★约束、虚位移和虚功的概念 2★★★★虚位移原理的应用 3

3 第十四章 虚位移原理 1 ★ ★ ★约束、虚位移和虚功的概念 2 ★ ★ ★ ★ 虚位移原理的应用

§14-1约束、虚位移和虚功 一、约束与约束方程 1对非自由体的某些位移起限制作用的周围物体 约束定义：限制质点或质点系运动的各种条件，称为 约束 2自由质点系：不受约束的质点系 3非自由质点系：受有约束的质点系 约束方程：对约束条件用数学公式表示，称为约束方程 例1 理想光滑面约束之-一一双面约束 77777777777777

 4 1 对非自由体的某些位移起限制作用的周围物体 §14-1 约束、虚位移和虚功 一、约束与约束方程 约束定义：限制质点或质点系运动的各种条件，称为 约束 约束方程：对约束条件用数学公式表示，称为约束方程 2 自由质点系：不受约束的质点系 3 非自由质点系：受有约束的质点系 例1 理想光滑面约束之-双面约束

§14-1约束、虚位移和虚功 例2图示平面内的单摆 摆杆是质点M的约束 摆杆对M的限制条件是？ x2+y2=12 A(x,y) 例题3图示曲柄连杆滑块机构的约束 x+2=2 2 A (xB-x4)+(yB-y4) 2 约束方程：表示限制条件的数学方程，称为约束方程

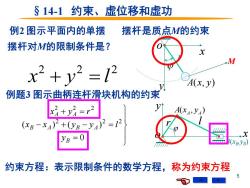
 5 o x y  A(x, y) l §14-1 约束、虚位移和虚功 例2 图示平面内的单摆 M 摆杆是质点M的约束 摆杆对M的限制条件是？ 2 2 2 x + y = l 约束方程：表示限制条件的数学方程，称为约束方程 例题3 图示曲柄连杆滑块机构的约束 o ( , ) A A A x y y x r l  B(xB ,yB )      = − + − = + = 0 ( ) ( ) 2 2 2 2 2 2 B B A B A A A y x x y y l x y r

§14-1约束、虚位移和虚功 例题4半径为R沿直线路面做纯滚动的车轮 y。=R xc=Ro X 例题5一摆长随时间变化的单摆 LL 该单摆的约束方程 X 1。-ut x2+y2=(亿。-ut)2 M(x,y) y

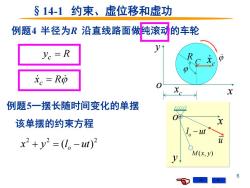
 6 §14-1 约束、虚位移和虚功 x o y R  c x C   c x  例题4 半径为R 沿直线路面做纯滚动的车轮 yc = R x  R  c = o x y M (x, y) u l ut o − 该单摆的约束方程 2 2 2 x y (l ut) + = o − 例题5一摆长随时间变化的单摆

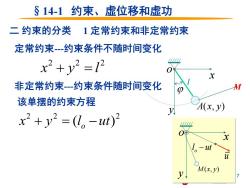
§14-1约束、虚位移和虚功 二约束的分类1定常约束和非定常约束 定常约束-约束条件不随时间变化 x2+y2=12 非定常约束-约束条件随时间变化 该单摆的约束方程 A(x,y) x2+y2=(L。-ut)2 x 1。-t M(x,y)

 7 o x y  A(x, y) l §14-1 约束、虚位移和虚功 二 约束的分类 1 定常约束和非定常约束 定常约束-约束条件不随时间变化 M 2 2 2 x + y = l 非定常约束-约束条件随时间变化 o x y M (x, y) u l ut o − 该单摆的约束方程 2 2 2 x y (l ut) + = o −

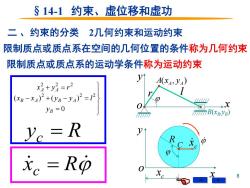
§14-1约束、虚位移和虚功 二、约束的分类2几何约束和运动约束 限制质点或质点系在空间的几何位置的条件称为几何约束 限制质点或质点系的运动学条件称为运动约束 x+=r2 A() (xB-x4)2+(0yB-y4)2=12 yB=0 →X T77B(xByB) y。 -R 12 R x=Ro

 8 §14-1 约束、虚位移和虚功 二 、约束的分类 2几何约束和运动约束 限制质点或质点系在空间的几何位置的条件称为几何约束 o ( , ) A A A x y y x r l  B(xB ,yB )      = − + − = + = 0 ( ) ( ) 2 2 2 2 2 2 B B A B A A A y x x y y l x y r yc = R 限制质点或质点系的运动学条件称为运动约束 x o y R  c x C   c x  x  R  c =

§14-1约束、虚位移和虚功 二约束的分类 3其他分类一完整约束和非完整约束 若约束方程的一般形式为 f, =0 (j=1,2,） 式中n为系统中质点的个数，s为约束方程的数目 显含坐标对时间的导数的约束方程是微分方程 如果这方程不可积分成有限形式，则相应的约束称为非完 整约束 如果这方程可积分成有限形式，则相应的约束称为完整约 束 xc=Ro xc=Ro

 9 §14-1 约束、虚位移和虚功 二 约束的分类 3 其他分类—完整约束和非完整约束 若约束方程的一般形式为 ( , , ;.; , , ; , , ,.; 1 1 1 1 1 1 f x y z x y z x y z j n n n    x , y , z ;t) = 0 n n n    ( j =1, 2,.,s) 式中n为系统中质点的个数，s为约束方程的数目 如果这方程不可积分成有限形式，则相应的约束称为非完 整约束 显含坐标对时间的导数的约束方程是微分方程 如果这方程可积分成有限形式，则相应的约束称为完整约 束 x  R  c = xc = R

§14-1约束、虚位移和虚功 3其他分类一完整约束和非完整约束 显含坐标对时间的导数的约束方程是微分方程 如果这方程不可积分成有限形式，则相应的约束称为非完 整约束 B 10

 10 §14-1 约束、虚位移和虚功 3 其他分类—完整约束和非完整约束 如果这方程不可积分成有限形式，则相应的约束称为非完 整约束 显含坐标对时间的导数的约束方程是微分方程 A B C