《理论力学》课程教学资源（PPT课件）动量矩定理

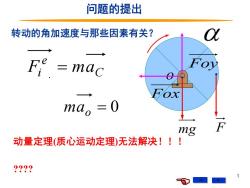
问题的提出 转动的角加速度与那些因素有关？ Fe =mac 00 mao =0 mg 动量定理（质心运动定理）无法解决！！！ ??? )

 1 问题的提出 F C o e Fi = ma . mao = 0 转动的角加速度与那些因素有关？  mgFoy Fox 动量定理(质心运动定理)无法解决！！！ ????

第十一章 动量矩定理 2

2 第十一章 动 量 矩 定 理

§11一4刚体对轴的转动惯量 总结和答疑 一 转动惯量是刚体转动惯性的度量 不仅与质量有关还与质量的分布情况有关 飞轮质量分布在轮缘的目的是？ 二转动惯量计算的主要方法 1牢记P288均质物体对其质心轴 2平行移轴定理 3组合法 4已知回转半径

 4 总结和答疑 §11－4 刚体对轴的转动惯量 不仅与质量有关还与质量的分布情况有关 飞轮质量分布在轮缘的目的是？ 2 平行移轴定理 3 组合法 4 已知回转半径 一 转动惯量是刚体转动惯性的度量 二 转动惯量计算的主要方法 1 牢记P288 均质物体对其质心轴

§11一4刚体对轴的转动惯量 二转动惯量的计算（重点掌握) 1查表法P288均质物体 2计算转动惯量的平行移轴定理（会应用) 内容 +m四 核心：两轴必须是相互平行；Jc必须是通过质心的 结论：在所有与质心轴平行的轴中， 刚体对质心轴的转动惯量最小 5

 5 2 计算转动惯量的平行移轴定理（会应用） 内容 2 J z  = J z c + md 核心：两轴必须是相互平行；JZC 必须是通过质心的 1 查表法 P288 均质物体 结论：在所有与质心轴平行的轴中， 二 转动惯量的计算（重点掌握） §11－4 刚体对轴的转动惯量 刚体对质心轴的转动惯量最小

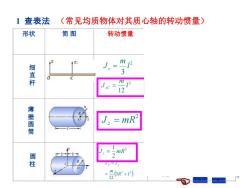
1查表法 (常见均质物体对其质心轴的转动惯量) 形状 简图 转动惯量 J.= m 12 细直杆 3 m J.c= 12 12 薄壁圆筒 :=mR2 R2 圆柱 2 =m6R2+） 12

 6 形状 简 图 转动惯量 惯性半径 体 积 细 直 杆 圆 柱 薄 壁 圆 筒 2 12 l m J zC = 2 3 l m J z = 2 J z = mR2 2 1 J z = mR ( ) 2 2 3 12 R l m J J x y = + =  z = R l l zC 0.289 2 3  = = l l z 0.578 3  = = 2Rlh R R z 0.707 2  = = ( ) 2 2 3 12 1 R l x y = +  =  R l 2  1 查表法 （常见均质物体对其质心轴的转动惯量）

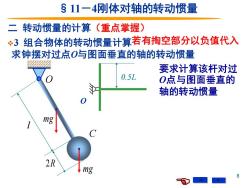
§11一4刚体对轴的转动惯量 二 转动惯量的计算（重点掌握） 3组合物体的转动惯量计算若有掏空部分以负值代入 求钟摆对过点0与图面垂直的轴的转动惯量 要求计算该杆对过 0.5L O点与图面垂直的 轴的转动惯量 mg C 2R mg

 8 二 转动惯量的计算（重点掌握） C O l 2R mg mg §11－4刚体对轴的转动惯量 求钟摆对过点O与图面垂直的轴的转动惯量 ❖3 组合物体的转动惯量计算若有掏空部分以负值代入 O 0.5L 要求计算该杆对过 O点与图面垂直的 轴的转动惯量

§11一4刚体对轴的转动惯量 二转动惯量的计算（重点掌握) ”4回转半径 →惯性半径（回转半径 白=吧的 应用：若已知回转半径可代入公式求出转动惯量

 9 二 转动惯量的计算（重点掌握） ❖ 4 回转半径 =  惯性半径(回转半径) m Jz  z 应用：若已知回转半径可代入公式求出转动惯量 2 z z J m=  §11－4刚体对轴的转动惯量

本次课的教学目标 2会计算刚体对轴的转动惯量 10

 10 本次课的教学目标 2 会计算刚体对轴的转动惯量

§11一1质点和质点系的动量矩 一、 质点的动量矩（基础) 1、质点对某点动量矩：质点在某瞬时的动量对O点之矩 定义为质点在该瞬时对0点的动量矩 Mo(mv) Mo(mv)=r×mv B Mo (mv v 作用在0点 大小 方向 联想？

 11 §11－1 质点和质点系的动量矩 一、质点的动量矩（基础） 1、质点对某点动量矩：质点在某瞬时的动量对O点之矩 M mv r mv O ( ) =  定义为质点在该瞬时对O点的动量矩 M (mv) O 联想？ 作用在O点 大小 方向 A mv B O r h M O (mv)

一、质点的动量矩 联想？ Mo(F)Mo(F)=r×F 作用在O点定位矢量 大小 M(F) 方向 联想到空间问题中力对轴的矩

 12 M F O ( ) O r MO(F) M F r F O ( ) =  作用在O点 定位矢量 大小 方向 h 联想？ 一、质点的动量矩 A F B 联想到空间问题中力对轴的矩