山东理工大学：《理论力学》课程教学资源（PPT课件）第2章 质点组力学

第2章质点组力学 2.1质点组 (1)质点组的内力与外力 1、质点组的概念 由多个质点构成，其中每一个质点的运动都可能与其他质点的位置和 运动有关，这种力学体系称为质点组。 2、质点组的内力与外力 质点组内部各质点间的相互作用称为质点组的内力 遵从牛顿第三定律，即内力总和为零 F=亡亡=0

质点组内部各质点间的相互作用称为质点组的内力 遵从牛顿第三定律，即内力总和为零      n i n j j i ji (i) F f 1 1 0   2.1 质点组 （1）质点组的内力与外力 由多个质点构成，其中每一个质点的运动都可能与其他质点的位置和 运动有关，这种力学体系称为质点组。 1、质点组的概念 2、质点组的内力与外力

第2章质点组力学 同时，对某参考点 20-立×0-0 3、解决质点组运动的途径 由于质点系内部相互的作用，运动彼此相互影响，往往使得求解过 程非常复杂，当质点系中质点的数目超过两个，运动的一般求解就比 较困难。因而在实际问题中，求解质点系整体运动特征不仅必要而且 成为可能。质点系动量、角动量、能量的定理及其守恒律就成为质点 系力学的研究核心

同时，对某参考点 0 1 1       n i (i) i i n i (i) Mi r F    3、解决质点组运动的途径 由于质点系内部相互的作用，运动彼此相互影响，往往使得求解过 程非常复杂，当质点系中质点的数目超过两个，运动的一般求解就比 较困难。因而在实际问题中，求解质点系整体运动特征不仅必要而且 成为可能。质点系动量、角动量、能量的定理及其守恒律就成为质点 系力学的研究核心

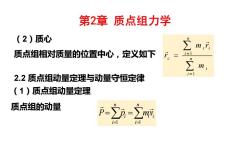
第2章质点组力学 (2)质心 m r 质点组相对质量的位置中心，定义如下 f。= 名 2.2质点组动量定理与动量守恒定律 (1)质点组动量定理 质点组的动量 p=∑n=∑

（2）质心 质点组相对质量的位置中心，定义如下      n i i n i i i c m m r r 1 1   2.2 质点组动量定理与动量守恒定律 （1）质点组动量定理 质点组的动量       n i i i n i i P p mv 1 1   

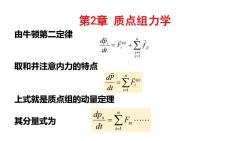
第2章质点组力学 由牛顿第二定律 =+2 d 取和并注意内力的特点 dt 上式就是质点组的动量定理 其分量式为 dp: =】 dt i=1

由牛顿第二定律      n j j i ji (e) i i F f dt dp 1    取和并注意内力的特点   n i (e) Fi dt dP 1   上式就是质点组的动量定理 其分量式为     n i ix x F dt dp 1

第2章质点组力学 或表示成微分式 dp=(∑F,o)d (2)质心运动定理 将质心定义式用于质点组的动量表示式，有 n-五立m成2所- d

或表示成微分式 dp  F dt (e)   i   （2）质心运动定理 将质心定义式用于质点组的动量表示式，有 c n i i i c n i i i n i i (mr ) mv dt d mr dt d P p mv             1 1 1

第2章质点组力学 代入质点组的动量定理 M=∑ 上式即为质心运动定理

代入质点组的动量定理    n i (e) c Fi Mr 1   上式即为质心运动定理

第2章质点组力学 (3)动量守恒定律 当2-0时，有 p=∑m,=恒矢 这时质心做惯性运动 若仅有∑F=0 则 p.=∑myn=常数 例p.89

（3）动量守恒定律 当 0 1    n i (e) Fi  时，有    n i i i P m v 1   恒矢 这时质心做惯性运动 若仅有  0 (e) Fix 则 px mivix 常数 例：p.89

第2章质点组力学 2.3动量矩定理及守恒律 1、对固定点O的动量矩定理 选参考系中一固定点0，由质点的动量矩定理 N+Nd 其中 Me=F×E@,M,=F×Fm 求和后有 注意到其中 29-2*0=0 i=1

2.3动量矩定理及守恒律 1、对固定点O的动量矩定理 选参考系中一固定点O，由质点的动量矩定理 dt dJ M M (i) i i (e) i      (i) i i (i) i (e) i i (e) Mi r F ,M r F                   n i i n i (i) i n i (e) i J dt d M M 1 1 1    其中 求和后有 注意到其中 0 1 1        n i (i) i i n i (i) Mi r F    J J n i i     1

第2章质点组力学 所以 上式就是质点组的动量矩定理 或写成微分式 dJ Mdt 在直角坐标系中

所以 dt dJ M n i (e) i     1 上式就是质点组的动量矩定理 或写成微分式 dJ Mdt    在直角坐标系中           n i i iz i iy n i mi yizi zi yi y F z F dt d 1 1 ( ) ( )

第2章质点组力学 (2)动量矩守恒律 由动量矩定理知，当 切-2=0 时，有 j=27,=2×m=恒天 i=l i=1 上式称为质点组的动量矩守恒定律 若仅当M,=0时，J=∑m(y,-2)=常数

（2）动量矩守恒律 由动量矩定理知，当 0 1    n i (e) M Mi   时，有    恒矢   n i i i i n i i J J r mv 1 1     上式称为质点组的动量矩守恒定律 若仅当 M x  0 时，     常数  n i x i i i i i J m y z z y 1 (   )