《理论力学》课程教学资源（PPT课件）虚位移原理

第十六章虚位移康理 条统的约束及其分类 口虚位移及其计算

第十六章 虚位移原理 • 系统的约束及其分类 • 虚位移及其计算

引 言 虚位移原理，是用分析的方法来研究任意 质点系的平衡问题。这部分内容称为分析静力 学。虚位移原理给出的平衡条件，对于任意质 点系的平衡都是必要与充分的，因此它是解决 质点系平衡问题的普遍原理。同时，将虚位移 原理和达朗伯原理相结合，可以导出动力学普 遍方程和拉格朗日方程，从而得到求解质点系 动力学问题的又一个普遍的方法

引 言 虚位移原理，是用分析的方法来研究任意 质点系的平衡问题。这部分内容称为分析静力 学。虚位移原理给出的平衡条件，对于任意质 点系的平衡都是必要与充分的，因此它是解决 质点系平衡问题的普遍原理。同时，将虚位移 原理和达朗伯原理相结合，可以导出动力学普 遍方程和拉格朗日方程，从而得到求解质点系 动力学问题的又一个普遍的方法

约束类型及分类 限制质点系中各质点的位置和运动的条件称为约束。表 示这些限制条件的表达式称为约束方程。根据约束形式及其 性质，约束可分以下类型： 一、几何约束与运动约束 限制质点或质点系在空间的几何位置的约束称为几何约束。 如： X M(x,y)x2+y2=12

限制质点系中各质点的位置和运动的条件称为约束。表 示这些限制条件的表达式称为约束方程。根据约束形式及其 性质，约束可分以下类型： 一、几何约束与运动约束 限制质点或质点系在空间的几何位置的约束称为几何约束。 如： O x y M (x, y)  l 2 2 2 x + y = l 约束类型及分类

A(YA) X T1777 x+y房=2 B(Xg:Yg) (XB-x)+(Ya-y4)2=12 YB=0 几何约束方程的一般形式为 f(x1,乃，21，.，xn,yn,2n)=0

O ( , ) A A A x y ( , ) B B B x y r l x y 0 ( ) ( ) 2 2 2 2 2 2 = − + − = + = B B A B A A A y x x y y l x y r 几何约束方程的一般形式为 f r (x1 , y1 ,z1 ,  , xn , yn ,zn ) = 0

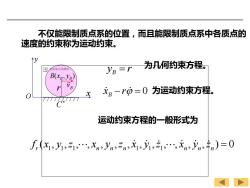
不仅能限制质点系的位置，而目能限制质点系中各质点的 速度的约束称为运动约束。 ↑y 为几何约束方程。 无法显示该图片 yB=r B() X xg一r0=0为运动约束方程。 运动约束方程的一般形式为 f(x1,y,1,Xn,yn,2n,元，y1,1,.,元n,少n,车n)=0

不仅能限制质点系的位置，而且能限制质点系中各质点的 速度的约束称为运动约束。 ( , ) B B B x y B v  O x y  C r y r 为几何约束方程。 B = x  B −r  = 0 为运动约束方程。 运动约束方程的一般形式为 f r (x1 , y1 ,z1 ,  , xn , yn ,zn , x  1 , y  1 ,z  1 ,  , x  n , y  n ,z  n ) = 0

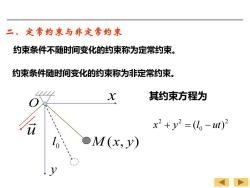
二、定常约束与非定常约束 约束条件不随时间变化的约束称为定常约束。 约束条件随时间变化的约束称为非定常约束。 X 其约束方程为 x2+y2=(-ut)2 OM(x,y)

二、定常约束与非定常约束 约束条件不随时间变化的约束称为定常约束。 约束条件随时间变化的约束称为非定常约束。 O x y M (x, y) u  0 l 其约束方程为 2 0 2 2 x + y = (l −ut)

非定常约束方程的一般形式为 f(X1,乃1,21，.，Xn,yn,2n,t)=0 三、双面约束与单面约束 同时限制质点某方向及相反方向运动的约束称为双面约 束。 只能限制质点某方向的运动，而不能限制相反方向运动 的约束称为单面约束。其约束方程的一般形式为 f(X1,1,21,.,Xn,yn,2n)<0

非定常约束方程的一般形式为 f r (x1 , y1 ,z1 ,  , xn , yn ,zn ,t) = 0 三、双面约束与单面约束 同时限制质点某方向及相反方向运动的约束称为双面约 束。 只能限制质点某方向的运动，而不能限制相反方向运动 的约束称为单面约束。其约束方程的一般形式为 f r (x1 , y1 ,z1 ,  , xn , yn ,zn )  0

四、完整约束与非完整约束 几何约束或其约束方程能够积分的运动约束称为 完整约束。 如果在约束方程中显含坐标对时间的导数，并且 不可以积分，这种约束称为非完整约束。 本章只研究定常的双面的完整的几何约束问题

四、完整约束与非完整约束 几何约束或其约束方程能够积分的运动约束称为 完整约束。 如果在约束方程中显含坐标对时间的导数，并且 不可以积分，这种约束称为非完整约束。 本章只研究定常的双面的完整的几何约束问题

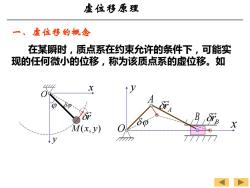
虚位移原理 、 虚位移的概念 在某瞬时，质点系在约束允许的条件下，可能实 现的任何微小的位移，称为该质点系的虚位移。如 M(x,y)

一、虚位移的概念 在某瞬时，质点系在约束允许的条件下，可能实 现的任何微小的位移，称为该质点系的虚位移。如 O x y M (x, y)   r   O A B x y A r   B r    虚位移原理

必须指出，虚位移和实位移都受约束的限制，是 约束所允许的位移，但二者是有区别的。实位移是在 一定的力作用下和给定的运动初始条件下，在一定的 时间内发生的位移，具有确定的方向，可能是微小值 也可能是有限值。而虚位移纯粹是一个几何概念，它 既不牵涉到系统的实际运动，也不涉及到力的作用， 与时间过程和运动的初始条件无关，它一定是微小值 在约束允许的条件下具有任意性。一个静止的质点或 质点系不会发生实位移，但可以有虚位移。在定常约 束的情况下，微小实位移必定是虚位移中的一个。在 非定常约束的情况下，实位移与虚位移没有关系

必须指出，虚位移和实位移都受约束的限制，是 约束所允许的位移，但二者是有区别的。实位移是在 一定的力作用下和给定的运动初始条件下，在一定的 时间内发生的位移，具有确定的方向，可能是微小值， 也可能是有限值。而虚位移纯粹是一个几何概念，它 既不牵涉到系统的实际运动，也不涉及到力的作用， 与时间过程和运动的初始条件无关，它一定是微小值， 在约束允许的条件下具有任意性。一个静止的质点或 质点系不会发生实位移，但可以有虚位移。在定常约 束的情况下，微小实位移必定是虚位移中的一个。在 非定常约束的情况下，实位移与虚位移没有关系