《理论力学》课程教学资源（PPT课件）第三章 空间力系

第三章 空间力系

第三章 空间力系

第三章： 空间力系 空间汇交力系 力对轴之矩和力对点之矩 空间力偶系 空间力系的简化 空间力系的平衡条件和平衡方程 物体的重心

第三章 空间力系 • 空间汇交力系 • 力对轴之矩和力对点之矩 • 空间力偶系 • 空间力系的简化 • 空间力系的平衡条件和平衡方程 • 物体的重心

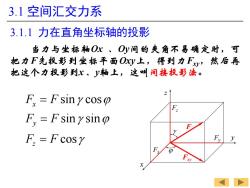
3.1空间汇交力系 3.1.1力在直角坐标轴的投影 当力与坐标轴Ox、Oy间的夹角不易确定时，可 把力F先投影到坐标平面Oy上，得到力Fy,然后再 把这个力投影到X、y轴上，这叫间接投影法。 F.=Fsiny cos F.=Fsinysin F.=Fcosy F

3.1 空间汇交力系 3.1.1 力在直角坐标轴的投影 y x z F Fx Fy Fz Fxy j g 当力与坐标轴Ox 、Oy间的夹角不易确定时，可 把力F先投影到坐标平面Oxy上，得到力Fxy，然后再 把这个力投影到x 、y轴上，这叫间接投影法。 sin cos sin sin cos x y z F F F F F F g j g j g = = =

3.1空间汇交力系 3.1.1力在直角坐标轴的投影 若已知力与正交坐标系Oyz三轴间夹角，则用直 接投影法 F.=Fcos(F,i) F F,=F cos(F,j) F.=Fcos(F,k)

3.1 空间汇交力系 y x z F Fx Fy Fz i k j 若已知力与正交坐标系Oxyz三轴间夹角，则用直 接投影法 cos( , ) cos( , ) cos( , ) x y z F F F F F F = = = F i F j F k 3.1.1 力在直角坐标轴的投影

3.1.2空间汇交力系的合成与平衡 1.合成 将平面汇交力条合成结果推广得： FR=F+E+.+Fn=ZF 或 FR=EFi+EF,j+Fk 合力的大小和方向为： F=V②F}+(②F)P+(∑E on-瓷an-装amR ΣF FR

1. 合成 将平面汇交力系合成结果推广得： R 1 2 n F F F F F = + + + =  i 合力的大小和方向为： 2 2 2 R ( ) ( ) ( ) F F F F =  +  +  x y z R R R R R R cos( , ) ,cos( , ) ,cos( , ) x y z F F F F F F    F i F j F k = = = 3.1.2 空间汇交力系的合成与平衡 或 F i j k R =  +  +  F F F x y z

3.1.2空间汇交力系的合成与平衡 2.平衡 空间汇交力系平衡的必要与充分条件是：该力条的合 力等于零。 FR=∑F=0 以解析式表示为： ∑F=0 ∑F=0 ∑F=0 空间汇交力条平衡的必要与充分条件是：该力系条力条 中所有各力在三个坐标轴上的投影的代数和分别等于 零

2. 平衡 空间汇交力系平衡的必要与充分条件是：该力系的合 力等于零。 R 0 F F =  =i 以解析式表示为： 3.1.2 空间汇交力系的合成与平衡 0 0 0 x y z F F F  =  =  = 空间汇交力系平衡的必要与充分条件是：该力系力系 中所有各力在三个坐标轴上的投影的代数和分别等于 零

例1重为P的物体用杆AB和位于同一水平面的绳索AC与AD支承，如图。已 知P=1000N,CE=ED=12cm,EA=24cm,B=45°，不计杆重；求绳索 的拉力和杆所受的力。 解：以较A为研究对象，受力如图。 X=0:T sin a-T sin a=0 Y=0:-Tc cosa-Tp cosa-Ssin B=0 B ∑Z=0:-S cos B-P=0 由几何关系： 24 2 cosa= V122+242 解得： S=-1414W Tc=T,=559N B

A B C D E P     A B C D E P     TD  TC  S  x y z 例1 重为P的物体用杆AB和位于同一水平面的绳索AC与AD支承，如图。已 知P＝1000N，CE＝ED＝12cm，EA＝24cm， ＝ 45° ，不计杆重；求绳索 的拉力和杆所受的力。 解：以铰A为研究对象，受力如图。  X = 0:TC sin  −TD sin  = 0 Y = 0: −TC cos −TD cos − S sin  = 0  Z = 0 : −S cos  − P = 0 由几何关系： 5 2 12 24 24 cos 2 2 = +  = 解得： S = −1414N TC = TD = 559N

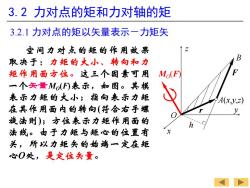
3.2力对点的矩和力对轴的矩 3.2.1力对点的矩以矢量表示一力矩矢 空间力对点的矩的作用效果 取决于：力矩的大小、转向和力 矩作用面方位。这三个因素可用 Mo(F) 一个矢量Mo(可表示，如图。其模 表示力矩的大小；指向表示力矩 A(x,y,2) 在其作用面内的转向（符合右手螺 y 旋法则)；方位表示力矩作用面的 法线。由于力矩与矩心的位置有 关，所以力矩矢的始端一定在矩 心O处，是定位矢量

3.2 力对点的矩和力对轴的矩 3.2.1 力对点的矩以矢量表示－力矩矢 x y z O M F O(F) r A(x,y,z) h B 空间力对点的矩的作用效果 取决于：力矩的大小、转向和力 矩作用面方位。这三个因素可用 一个矢量MO(F)表示，如图。其模 表示力矩的大小；指向表示力矩 在其作用面内的转向(符合右手螺 旋法则)；方位表示力矩作用面的 法线。由于力矩与矩心的位置有 关，所以力矩矢的始端一定在矩 心O处，是定位矢量

3.2.1力对点的矩以矢量表示一力矩矢 以r表示力作用点A的矢径，则 B Mo(F)=rxF Mo(F) 以矩心O为原点建立坐标系，则 r=xi+yj+zk A(x.y,) F=Fi+Fj+Fk Mo(F)=rxF=x y z =(yF:-zF,)i+(zF-xF.)j+(xF,-yF,)k

3.2.1 力对点的矩以矢量表示－力矩矢 以r表示力作用点A的矢径，则 M F r F O ( ) =  以矩心O为原点建立坐标系，则 x y z x y z F F F = + + = + + r i j k F i j k ( ) ( ) ( ) ( ) O x y z z y x z y x x y z F F F yF zF zF xF xF yF =  = − + − + − i j k M F r F = i j k x y z O M F O(F) r A(x,y,z) h B j i k

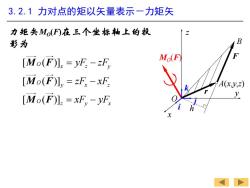
3.2.1力对点的矩以矢量表示一力矩矢 力矩矢Mo(F在三个坐标轴上的投 影为 B [Mo(F)]=yF:-F Mo(F [Mo(F)〗，=zF-xF A(xy,) [Mo(F)]:=xF,-yF

3.2.1 力对点的矩以矢量表示－力矩矢 力矩矢MO(F)在三个坐标轴上的投 影为 [ ( )] [ ( )] [ ( )] O x z y O y x z O z y x yF zF zF xF xF yF = − = − = − M F M F M F x y z O M F O(F) r A(x,y,z) h B j i k