《理论力学》课程教学资源（PPT课件）刚体的平面运动

第八章 则体的平百运动

3.平面平行远动 在运动中，则体上的任意一点与某一固定平面始 终保持相等的距离，这种运动称为平面运动

在运动中，刚体上的任意一点与某一固定平面始 终保持相等的距离，这种运动称为平面运动

8.1刚体平面运动概述和运动分解 则体上每一点都在与固定 平面M平行的平面内运动。 9A1 若作一平面N与平面M平行， 并以此去载割则体得一平 面图形S。可知该平面图 形S始终在平面N内运动。 因而垂直于图形S的任一条 直线A1A2必然作平动。 A1A2的运动可用其与图形 12 S的交点A的运动来替代。 刷体的平面运动可以简化为平面图形在其自身平面S内的运动

8.1 刚体平面运动概述和运动分解 M N S A1 A2 A 刚体上每一点都在与固定 平面M平行的平面内运动。 若作一平面N与平面M平行, 并以此去截割刚体得一平 面图形S。 可知该平面图 形S始终在平面N内运动。 因而垂直于图形S的任一条 直线A1A2必然作平动。 A1A2的运动可用其与图形 S的交点 A的运动来替代。 刚体的平面运动可以简化为平面图形在其自身平面S内的运动

8.1刚体平面运动概述和运动分解 平面图形S在其平面上的位置完 全可由图形内任意线段O'M的位置来 确定，而要确定此线段的位置，只需 S 确定线段上任一点O'的位置和线段 O'M与固定坐标轴Ox间的夹角0即可。 点O'的坐标和p角都是时间的函数， 即 xo=(1),yo=12(1),p=/3(1) 这就是平面图形的运动方程。 平面图形的运动方程可由两部分组成：一部分是平面图形 接点0'的运动方程X0=f(),y0=()的平移，设有转动；另一部 分是绕0'点转角为p=5()的转动

1 2 3 ( ), ( ), ( ) O O x f t y f t  f t      这就是平面图形的运动方程。 S M O' y x O 8.1 刚体平面运动概述和运动分解  平面图形S在其平面上的位置完 全可由图形内任意线段O'M的位置来 确定，而要确定此线段的位置，只需 确定线段上任一点O'的位置和线段 O'M与固定坐标轴Ox间的夹角即可。 点O'的坐标和角都是时间的函数， 即 平面图形的运动方程可由两部分组成：一部分是平面图形 按点O'的运动方程xO' = f1(t), yO' = f2(t)的平移，没有转动；另一部 分是绕O'点转角为 = f3(t)的转动

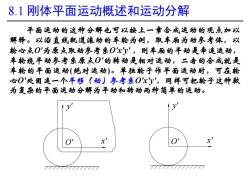
8.1刚体平面运动概述和运动分解 平面运动的这种分解也可以接上一章合成运动的观点加以 解释。以沿直线轨道滚动的车轮为倒，取车厢为动参考体，以 轮心点O'为原点取动参考系Oxy',则车厢的平动是牵连运动， 车轮绕平动参考系原点O'的转动是相对运动，二者的合成就是 车轮的平面运动（绝对运动）。单独轮子作平面运动时，可在轮 心O'处固连一个平移（动）参考集Oxy',同样可把轮子这种较 为复杂的平面运动分解为平动和转动两种简单的运动。 x x' 7777777777777 77777777777777

8.1 刚体平面运动概述和运动分解 平面运动的这种分解也可以按上一章合成运动的观点加以 解释。以沿直线轨道滚动的车轮为例，取车厢为动参考体，以 轮心点O'为原点取动参考系O'x'y' ，则车厢的平动是牵连运动， 车轮绕平动参考系原点O'的转动是相对运动，二者的合成就是 车轮的平面运动(绝对运动)。单独轮子作平面运动时，可在轮 心O'处固连一个平移（动）参考系O'x'y' ，同样可把轮子这种较 为复杂的平面运动分解为平动和转动两种简单的运动。 y' O x' ' y' O x'

8.1刚体平面运动概述和运动分解 对于任意的平面运动， 可在平面图形上任取一点O', 称为基点。在这一点假想地 安上一个平移参考条Oxy'; 平面图形运动时，动坐标轴 方向始终保持不变，可令其 分别平行于定坐标轴Ox和 Oy。于是平面图形的平面 o' 运动可看成为随同基点的平 移和随基点转动这两部分运 动的合成

8.1 刚体平面运动概述和运动分解 对于任意的平面运动， 可在平面图形上任取一点O' ， 称为基点。在这一点假想地 安上一个平移参考系O'x'y'； 平面图形运动时，动坐标轴 方向始终保持不变，可令其 分别平行于定坐标轴Ox和 Oy 。于是平面图形的平面 运动可看成为随同基点的平 移和随基点转动这两部分运 动的合成。 y' O x' ' y x O

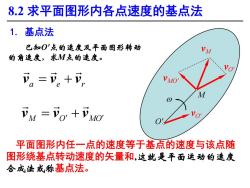
8.2求平面图形内各点速度的基点法 1.基点法 已知O'点的速度及平面图形转动 的角速度，求M点的速度。 可a=可。+， M=O+MO 平面图形内任一点的速度等于基点的速度与该点随 图形绕基点转动速度的矢量和，这就是平面运动的速度 合成法或称基点法

O' M 平面图形内任一点的速度等于基点的速度与该点随 图形绕基点转动速度的矢量和,这就是平面运动的速度 合成法或称基点法。 1. 基点法 已知O'点的速度及平面图形转动 的角速度，求M点的速度。 8.2 求平面图形内各点速度的基点法 w vM vO' vMO' vO' a  e  r    v v v M  O  MO    v v v

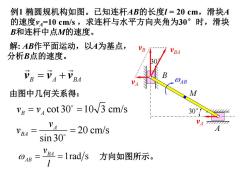
例1椭圆规机构如图。已知连杆AB的长度l=20cm,滑块A 的速度v4=10cm/s,求连杆与水平方向夹角为30°时，滑块 B和连杆中点M的速度。 解：AB作平面运动，以A为基点， VB 分析B点的速度。 VBA Va =VA+Vad VA AB 由图中几何关系得： M Vg =v cot 30=10v3 cm/s 309 VBA= =20cm/s sin30° 4-lrad/s方向如图所示。 1

例1 椭圆规机构如图。已知连杆AB的长度l = 20 cm，滑块A 的速度vA=10 cm/s ，求连杆与水平方向夹角为30°时，滑块 B和连杆中点M的速度。 解: AB作平面运动，以A为基点， 分析B点的速度。 cot 30 10 3 cm/s B A v  v   由图中几何关系得： 1rad s BA AB v l w   方向如图所示。 A vA vA vB vBA B wAB 30° B  A  BA    v v v M 20 cm/s sin 30 A BA v v    30°

以A为基点，则M点的速度为 下M=A+MM 将各矢量投影到坐标轴上得： xX:-Vu cosa =-V+Vva sin 30 y:Vy sina=VMa cos30° 30°， 解之得 Vy =10cm/s tana=√3 =60°

以A为基点，则M点的速度为 将各矢量投影到坐标轴上得： : cos sin 30 M A MA x  v   v  v  : sin cos30 M MA y v   v  解之得 10cm s M v  tan  3    60 A vA vA vMA B wAB 30° M vM M  A  MA    v v v x y 

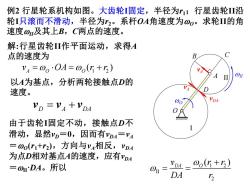
例2行星轮系机构如图。大齿轮固定，半径为1；行星齿轮沿 轮I只滚而不滑动，半径为r2。系杆OA角速度为oo。求轮II的角 速度ou及其上B,C两点的速度。 解：行星齿轮I作平面运动，求得A 点的速度为 B v4=0oOA=0o(+3) 以A为基点，分析两轮接触点D的 速度。 VDA VD =VA+VDA 由于齿轮I固定不动，接触点D不 滑动，显然yD=0,因而有ypA=vA =oo(r1tr2),方向与y4相反，VDA 为点D相对基点A的速度，应有DA =0IDA。所以 Vp4=0o(G+5) DA 3

例2 行星轮系机构如图。大齿轮I固定，半径为r1；行星齿轮II沿 轮I只滚而不滑动，半径为r2。系杆OA角速度为wO。求轮II的角 速度wII及其上B，C两点的速度。 解:行星齿轮II作平面运动，求得A 点的速度为 vA wO D  A  DA v v v O D A B C vA vDA wII I II 以A为基点，分析两轮接触点D的 速度。 1 2 ( ) A O O v w OA w r  r 由于齿轮I固定不动，接触点D不 滑动，显然vD＝0，因而有vDA＝vA ＝w O(r1+r2)，方向与vA相反，vDA 为点D相对基点A的速度，应有vDA ＝wII·DA。所以 1 2 II 2 ( ) DA O v r r DA r w w   