《理论力学》课程教学资源（PPT课件）动能定理

第十二章 动能定理 ·力的功 ·质点和质点系的动能 ·动能定理 ·善遍定理的综合应用举创 。功率·功率方程·机械效率

第十二章 动能定理 • 力的功 • 质点和质点系的动能 • 动能定理 • 普遍定理的综合应用举例 • 功率·功率方程·机械效率

引言 前两章是以动量和冲量为基础，建立了质点或质 点条运动量的变化与外力及外力作用时问之问的关系。 本章以功和动能为基础，建立质点或质点系动能的改 变和力的功之间的关系，即动能定理。不同于动量定 理和动量矩定理，动能定理是从能量的角度来分析质 点和质点系的动力学问题，有时是更为方便和有效的。 同时，它还可以建立机械运动与其它形式运动之间的 联条。 在介绍动能定理之前，先介绍有关的物理量：功 与动能

前两章是以动量和冲量为基础，建立了质点或质 点系运动量的变化与外力及外力作用时间之间的关系。 本章以功和动能为基础，建立质点或质点系动能的改 变和力的功之间的关系，即动能定理。不同于动量定 理和动量矩定理，动能定理是从能量的角度来分析质 点和质点系的动力学问题，有时是更为方便和有效的。 同时，它还可以建立机械运动与其它形式运动之间的 联系。 在介绍动能定理之前，先介绍有关的物理量：功 与动能。 引言

12.1力的功 12.1.1常力的功 设物体在常力F作用下沿直线走过路程5，如图， 则力所作的功W定义为 W-Fcos0.s=F.s 功是代数量。宅表示力在一段路程上的累积作用效应， 因此功为累积量。在国际单位制中，功的单位为：J (焦耳)，1J=1Nm

12.1.1 常力的功 设物体在常力F作用下沿直线走过路程s，如图， 则力所作的功W定义为 W F s =  =  cos F s 功是代数量。它表示力在一段路程上的累积作用效应， 因此功为累积量。在国际单位制中，功的单位为：J (焦耳), 1J＝1 N·m。 12.1力的功

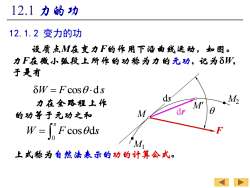
12.1力的功 12.1.2变力的功 设质点M在变力F的作用下沿曲线运动，如图。 力F在微小孤段上所作的功称为力的元功，记为δW, 于是有 δW=Fcosθ.ds 力在全路程上作 M2 的功等于元功之和 M W=[Fcosds 上式称为自然法表示的功的计算会式

12.1.2 变力的功 设质点M在变力F的作用下沿曲线运动，如图。 力F在微小弧段上所作的功称为力的元功, 记为dW, 于是有 δW F s =  cos d  12.1 力的功 M' M1 M2  ds M dr F 力在全路程上作 的功等于元功之和 0 cos d s W F s =   上式称为自然法表示的功的计算公式

12.1力的功 上两式可写成关量点乘积形式 =∫下d 称为矢径法表示的功的计算公式。 在直角坐标系中 F=Fi+Fj+k,dr=dxi+dyj+dzk δW=Fdx+Fdy+Fdz W-(Fdx+F,dy+Fd=) 上式称为直角坐标法表示的功的计算公式，也称为功 的解析表达式

δW =  F rd 2 1 d M M W =   F r 称为矢径法表示的功的计算公式。 在直角坐标系中 d d d d F i j k, r i j k = + + = + + F F F x y z x y z δ d d d W F x F y F z = + + x y z 2 1 ( d d d ) M x y z M W F x F y F z = + +  12.1 力的功 上两式可写成矢量点乘积形式 上式称为直角坐标法表示的功的计算公式，也称为功 的解析表达式

12.1力的功 12.1.3常见力的功 1)重力的功 M M 设质点的质量为m,在重力 作用下从M1运动到M2。建立如 21 mg 图坐标，则 22 F=0,F=0,F=-ng 代入功的解析表达式得 W2=∫(-mg)dz=mg(,-2）

1) 重力的功 设质点的质量为m，在重力 作用下从M1运动到M2。建立如 图坐标，则 0, 0, F F F mg x y z = = = − 代入功的解析表达式得 2 1 12 1 2 ( )d ( ) z z W mg z mg z z = − = −  12.1.3 常见力的功 12.1 力的功 M1 M2 M mg z1 z2 O x y z

常见力的功 对于质点系，其重力所作的功为 W2=∑m,8(21-22） =(∑m,1-∑m,22)g =(MEcI-MEc2)g =Mg(2c1-2c2) 由此可见，重力的功仅与重心的始末位置有关，而与 重心走过的路径无关

对于质点系，其重力所作的功为 12 1 2 1 2 1 2 1 2 ( ) ( ) ( ) ( ) i i i i i i i C C C C W m g z z m z m z g Mz Mz g Mg z z =  − =  −  = − = − 由此可见，重力的功仅与重心的始末位置有关，而与 重心走过的路径无关。 常见力的功

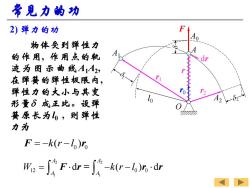
常见力的功 2)弹力的功 0 物体受到弹性力 的作用，作用点的轨 迹为图示曲线A1A2, 在弹簧的弹性极限内， 弹性力的大小与其变 形量6成正比。设弹 簧原长为，则弹性 力为 F=-k(r-lo)to W2=∫Fdr=∫-k(r-6)dr

2 ) 弹力的功 物体受到弹性力 的作用 , 作用点的轨 迹 为图 示曲线 A 1 A 2 , 在弹簧的弹性极限内 , 弹性力的大小与其变 形量 d 成正比 。设弹 簧原长为 l0 , 则弹性 力为 0 0 F r = − − k r l ( ) 2 2 1 1 12 0 0 d ( ) d A A A A W k r l =  − −    F r = r r A 1 A 2 r2 r 1 l 0 Or0r A d F A 0 d r 常见力的功

常见力的功 因为 _L.dr =2r 于是 =-6d=[G-4-4门 或 W,=号(82-) 2 弹性力作的功只与弹簧在初始和末了位置的变形量有 关，与力的作用点A的轨迹形状无关

于是 2 1 2 2 12 0 1 0 2 0 1 ( )d ( ) ( ) 2 r r W k r l r k r l r l = − − = − − −      或 ( ) 2 1 2 2 2 W12 = k d 1 −d 因为 2 0 1 1 d d d( ) d d 2 2 r r r r r  =  =  = = r r r r r r 弹性力作的功只与弹簧在初始和末了位置的变形量有 关，与力的作用点A的轨迹形状无关。 常见力的功

常见力的功 3)定轴转动刚体上作用力的功 设作用在定轴转动则体上A点的力为F, 将该力分解为F、Fn和Fb, F=Fcose 当则体转动时，转角p与孤长5的关系为 ds Rdo R为力作用点A到轴的垂距。力F的元 功为 W=F.dr=Fds=FRdo=M.do 力F在则体从角四转到2所作的功为 m。=M.do M,可视为作用在刚体上的力偶

3) 定轴转动刚体上作用力的功 设作用在定轴转动刚体上A点的力为F, 将该力分解为Ft、Fn和Fb， 常见力的功 当刚体转动时，转角j与弧长s的关系为 t F = F cos d d s R = j R为力作用点A到轴的垂距。力F的元 功为 t t δ d d d d W F s F R M =  = = F r = j jz Ft F r Fb Fn O z O1 A  力F在刚体从角j1转到j2所作的功为 2 1 12 d W Mz j j = j  Mz可视为作用在刚体上的力偶