《理论力学》课程教学资源（PPT课件）第 7 章 点的合成运动

第7章 点的合成运动 7.1相对运动·牵连运动·绝对运动 7.2点的速度合成定理 7.3点的如速度合成定理

第 7 章 点的合成运动 7.1 相对运动·牵连运动·绝对运动 7.2 点的速度合成定理 7.3 点的加速度合成定理

7.1相对运动牵连运动绝对运动 通过观察可以发现，物体对一参考体的运动可以由几个运动 组合而成。例如，在上述的例子中，车轮上的点M是沿旋轮线运 动，但是知果以车厢作为参考体，则点M对于车厢的运动是简单 的圆周运动，车厢对于地面的运动是简单的平动。这样，轮缘上 一点的运动就可以看成为两个简单运动的合成，即点M相对于车 厢作圆周运动，同时车厢对地面作平动。于是，相对于某一参考 体的运动可由相对于其它参考体的几个运动组合而成，称这种运 动为合成运动

x y' x' y o' o M v 7.1 相对运动·牵连运动·绝对运动 通过观察可以发现，物体对一参考体的运动可以由几个运动 组合而成。例如，在上述的例子中，车轮上的点M是沿旋轮线运 动，但是如果以车厢作为参考体，则点M对于车厢的运动是简单 的圆周运动，车厢对于地面的运动是简单的平动。这样，轮缘上 一点的运动就可以看成为两个简单运动的合成，即点M相对于车 厢作圆周运动，同时车厢对地面作平动。于是，相对于某一参考 体的运动可由相对于其它参考体的几个运动组合而成，称这种运 动为合成运动

7.1相对运动牵连运动绝对运动 习惯上把固定在地球上的坐标系称为定参考系， 以0心y坐标系表示；固定在其它相对于地球运动的参考 体上的坐标象称为动参考系，以0xy'坐标条表示。 用点的合成运动理论分析点的运动时，必须选定两 个参考条，区分三种运动： ()动点相对于定参考条的运动，称为绝对运动； (2)动点相对于动参考条的运动，称为相对运动； (③)动参考条相对于定参考条的运动，称为牵连运动

习惯上把固定在地球上的坐标系称为定参考系， 以oxy坐标系表示；固定在其它相对于地球运动的参考 体上的坐标系称为动参考系，以o'x'y'坐标系表示。 7.1 相对运动·牵连运动·绝对运动 用点的合成运动理论分析点的运动时，必须选定两 个参考系，区分三种运动： (1) 动点相对于定参考系的运动，称为绝对运动； (2) 动点相对于动参考系的运动，称为相对运动； (3) 动参考系相对于定参考系的运动，称为牵连运动

7.1相对运动牵连运动绝对运动 牵连运动 定参考系 动参考条 绝对运动 相对运动 动点 一点、二系、三运动

定参考系 动参考系 动点 牵连运动 一点、二系、三运动 7.1 相对运动·牵连运动·绝对运动

7.1相对运动牵连运动绝对运动 (1)动点相对于定参考系的速度、加速度和轨迹， 称为动点的绝对速度ya、绝对加速度1和绝对轨迹。 (2)动点相对于动参考条的速度、如速度和轨迹， 称为动点的相对速度y,、相对加速度·，和相对轨迹。 由于动参考条的运动是则体的运动而不是一个点 的运动，所以除非动参考条作平移，否则其上各点的 运动都不完全相同。因为动参考条与动点直接相关的 是动参考系上与动点相重合的那一点（牵连点），因此 定义： 在动参考系上与动点相重合的那一点（牵连点）的 速度和加速度称为动点的率连速度（用v表示）和牵连 如速度（用ae表示）

(1) 动点相对于定参考系的速度、加速度和轨迹， 称为动点的绝对速度va、绝对加速度aa和绝对轨迹。 (2) 动点相对于动参考系的速度、加速度和轨迹， 称为动点的相对速度vr、相对加速度ar和相对轨迹。 7.1 相对运动·牵连运动·绝对运动 由于动参考系的运动是刚体的运动而不是一个点 的运动，所以除非动参考系作平移，否则其上各点的 运动都不完全相同。因为动参考系与动点直接相关的 是动参考系上与动点相重合的那一点(牵连点)，因此 定义： 在动参考系上与动点相重合的那一点(牵连点)的 速度和加速度称为动点的牵连速度(用ve表示)和牵连 加速度(用ae表示)

例如图杆长1，绕0轴以角速 度转动，圆盘半径为r,绕 轴角速度转动求圆盘边 e2 缘和点的牵连速度和加速 度。 解：静系取在地面上，动系 取在杆上，则 vel (1-r)@ de =(1-r)o- 重点要弄清楚牵 ye2=V7+r20 连点的概念 a2=V7+r2o2

例 如图杆长l，绕O轴以角速 度 转动，圆盘半径为r，绕 轴以角速度 转动。求圆盘边 缘 和 点的牵连速度和加速 度。 o    M1 M2 解：静系取在地面上，动系 取在杆上，则 ve1 = (l − r) 2 1 ae = (l − r)  2 2 2 v l r e = + 2 2 2 ae2 = l + r  o o    M1 M2 e1 v  e1 a  e2 v  e2 a  重点要弄清楚牵 连点的概念

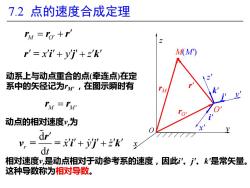
7.2点的速度合成定理 ry =To +r' r'=x'i'+yi+z'k M(M) 动系上与动点重合的点（牵连点）在定 系中的矢径记为rM,在图示瞬时有 ry =rM 动点的相对速度y,为 dr' y,= ='++k dt 相对速度v,是动点相对于动参考系的速度，因此”、'、k是常矢量。 这种导数称为相对导数

7.2 点的速度合成定理 rM rO' r' M(M') O' j' k' i' y' z' x' x y z O M O r r r = +  r = i j k        x y z + + M M =  r r d d r x y z t        + + r v = = i j k 动系上与动点重合的点(牵连点)在定 系中的矢径记为rM' ，在图示瞬时有 相对速度vr是动点相对于动参考系的速度，因此i'、j'、k'是常矢量。 这种导数称为相对导数。 动点的相对速度vr为

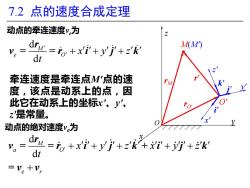
7.2点的速度合成定理 动点的牵连速度y为 drr=to+xi+yk M(M) dt 牵连速度是牵连点M'点的速 度，该点是动系上的点，因 此它在动系上的坐标'、y'、 z是常量。 动点的绝对速度为 4=。+x7+y+zW年置+训+k dt =Ve+v

7.2 点的速度合成定理 rM rO' r' M(M') O' j' k' i' y' z' x' x y z O d d M e O x y z t   + + +       r v = = r i j k d d M a O e r x y z x y z t  + + + + +             + r v = = r i j k + i j k = v v 动点的牵连速度ve为 牵连速度是牵连点M'点的速 度，该点是动系上的点，因 此它在动系上的坐标x'、y'、 z'是常量。 动点的绝对速度va为

7.2点的速度合成定理 Va =Ve +Vr 即：动点在某一瞬时的绝对速 度等于它在该瞬时的牵连速度 与相对速度的矢量和。这就是 点的速度合成定理

v v v a e r = + 即：动点在某一瞬时的绝对速 度等于它在该瞬时的牵连速度 与相对速度的矢量和。这就是 点的速度合成定理。 7.2 点的速度合成定理

7.2点的速度合成定理 处理具体问题时应注意： ()选取动点、动参考系和定参考系。 动点和动系应分别选择在两个不同的刚体上。 动点和动系的选择应使相对运动的轨迹简单直观。 在有的机构中，一个构件上总有一个点被另一个构件 所束。这时，以被约束的点作为动点，在约束动点 的构件上建立动系，相对运动轨迹便是约束构件的轮 廓线或者约束动点的轨道。 (2)应用速度合成定理时，可利用速度平行四边形中的 几何关系解出未知数。也可以采用投影法：即等式左 右两边同时对某一轴进行投影，投影的结果相等

处理具体问题时应注意： (1) 选取动点、动参考系和定参考系。 (2) 应用速度合成定理时,可利用速度平行四边形中的 几何关系解出未知数。也可以采用投影法：即等式左 右两边同时对某一轴进行投影，投影的结果相等。 动点和动系应分别选择在两个不同的刚体上。 动点和动系的选择应使相对运动的轨迹简单直观。 7.2 点的速度合成定理 在有的机构中，一个构件上总有一个点被另一个构件 所约束。这时，以被约束的点作为动点，在约束动点 的构件上建立动系，相对运动轨迹便是约束构件的轮 廓线或者约束动点的轨道