《理论力学》课程教学资源（PPT课件）动量定理

10动量定理 口动量与冲量 」动量定理 □质心运动定理 用质点运动微分方程解决质点系动力学问题在数学上会遇到很大困唯。 在许多工程问题中并不需要求出每个质点的运动规律，而是只需知道质点 系整体的运动特征就够了。 动力学普遍定理包括动量定理、动量矩定理、动能定理。这些定理建 立了表现运动特征的量（动量、动量矩、动能）和表现力作用效果的量 (冲量、冲量矩、功）之间的关系。 在应用普追定理解决实际问题时，不仅运算简单，而且各个量都具有 明确的物理意义，便于更深入地研究机械运动的规律

10 动量定理 动量与冲量 动量定理 质心运动定理 用质点运动微分方程解决质点系动力学问题在数学上会遇到很大困难。 在许多工程问题中并不需要求出每个质点的运动规律，而是只需知道质点 系整体的运动特征就够了。 动力学普遍定理包括动量定理、动量矩定理、动能定理。这些定理建 立了表现运动特征的量（动量、动量矩、动能）和表现力作用效果的量 （冲量、冲量矩、功）之间的关系。 在应用普遍定理解决实际问题时，不仅运算简单，而且各个量都具有 明确的物理意义，便于更深入地研究机械运动的规律

10.1动量与冲量 10.1.1动量 1)质点的动量 质点的质量与速度的乘积称为质点的动量， 记为mv。 动量是失量，方向与速度方向相同。动量的单位为 kgm/s。 2)质点系的动量 质点系中各质点动量的矢量和称为质点系的 动量。 D=∑m

10.1 动量与冲量 10.1.1 动量 1）质点的动量 质点的质量与速度的乘积称为质点的动量， 记为mv。 动量是矢量，方向与速度方向相同。动量的单位为 kg•m/s。 2）质点系的动量 质点系中各质点动量的矢量和称为质点系的 动量。  mi i p v  

动量 3)质心及用质心速度求质点系动量 定义质点系质量中心（质心）C的失径 则 p=∑m9,=Σm d元_d工mf t dt d (mic)=mvc 质点系的动量等于质 dt 点系的质量与质心速 度的乘积

3）质心及用质心速度求质点系动量 定义质点系质量中心(质心) C 的矢径 d d d d d ( ) d i i i i i i C C m m m t t m m t         r p v r r v       则 质点系的动量等于质 点系的质量与质心速 度的乘积。 动量

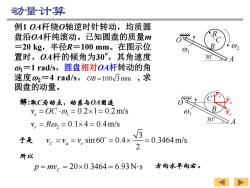
动量计算 例1OA杆绕O轴逆时针转动，均质圆 盘沿OA杆纯滚动。已知圆盘的质量m =20kg,半径R=100mm。在图示位 02 置时，OA杆的倾角为30°，其角速度 302 o1=1rad/s,圆盘相对OA杆转动的角 速度o2=4rad/s,OB=100√5mm,求 圆盘的动量。 解：取C为动点，动系与OA固连 v。=OC·o=0.2×1=0.2m/s 30° y,=R02=0.1×4=0.4m/s A 于是 =,=ysm60=04× -=0.3464m/s 2 所以 p=mvc=20×0.3464=6.93Ns方向水平向右

O A  30 1 B 2 C R e v  a v  r v  A  30 B C O 1 例1 OA杆绕O轴逆时针转动，均质圆 盘沿OA杆纯滚动。已知圆盘的质量m ＝20 kg，半径R＝100 mm。在图示位 置时，OA杆的倾角为30 o ，其角速度 1＝1 rad/s，圆盘相对OA杆转动的角 速度2＝4 rad/s， , 求 圆盘的动量。 OB 100 3 mm 1 2 0.2 1 0.2m/s 0.1 4 0.4m/s e r v OC v R            3 sin 60 0.4 0.3464m/s 2 C a r v  v  v    于是  所以 20 0.3464 6.93N s C p  mv     方向水平向右。 动量计算 解:取C为动点，动系与OA固连

动量计算 例2、椭圆规机构的规尺AB的质量为 2m1,曲柄OC的质量为m1,滑块A和 B的的质量均为m2。已知OC=AC= 21 CB=1。曲柄和规尺均为均质细直杆。 曲柄以角速度o转动。求机构的动量。 ot 解1：由质点系动量公式有 p=2m Vc +mvc +mv+m ve 建立如图直角坐标系，则动量的投影为 p:=-2m Vc sin ot-m vci sin ot-m2v =-2mlo sinot-m sinot-m,2lo sin ot 二1 om4m)sin of

x y O t  C C A B C1 B m v  2 A m v  2 C m v  2 1 1 C1 m v  例2、椭圆规机构的规尺AB的质量为 2m1，曲柄OC的质量为m1，滑块A和 B的的质量均为m2。已知OC＝AC＝ CB＝l。曲柄和规尺均为均质细直杆。 曲柄以角速度转动。求机构的动量。 解1：由质点系动量公式有 1 1 1 2 2 2  m C  m C  m A  m B p v v v v      建立如图直角坐标系，则动量的投影为 m m t l t m l t l m l t m p m v t m v t m v x C C A           (5 4 )sin 2 sin 2 sin 2 2 sin 2 sin sin 1 2 1 1 2 1 1 1 2            动量计算

py =2m Vc cos wt +mvc cos ot +mvB lo 2mo comco+m.2lo.coso (5m +4m.)cosot y 所以机构动量的大小和方向为 p=+-(5m+4m） B 2% cos(元，i)=cosP:=sinot p

m m t l t m l t l m l t m p m v t m v t m v y C C B           (5 4 ) cos 2 cos 2 cos 2 2 cos 2 cos cos 1 2 1 1 2 1 1 1 2         所以机构动量的大小和方向为 (5 4 ) 2 1 2 2 2 m m l p  px  py    t p p p i x cos( , )  cos  sin   x y O t  C C A B C1 B m v  2 A m v  2 C m v  2 1 1 C1 m v 

解2： y D PaB +Pa+Pe=2(m+m2)c P2=Poc =mVc B p=p+p2=PaB +Pa+PB+Poc C =2m,+m)成e+m2 =5m+4m城 因为vc=lo 得 p=25m+4m,l0 方向为C点速度的方向

x yO t  C C A B C1 1 p p2  C C C AB A B OC m m v v m m v m p p p p p p p           (5 4 ) 21 2 2( ) 1 2 1 2 1 1 2            解2：1 1 2 2 1 1 2( ) AB A B C OC C p p p p m m v p p m v                vC  l p (5m 4m )l 21  1  2 方向为C点速度的方向。 因为得

例3、两均质杆OA和AB质量为m,长为L,铰接于A。图示位 置时，OA杆的角速度为0，AB杆相对OA杆的角速度亦为o. 求此瞬时系统的动量。 解：由刚体系统的动量公式 p=mVc+m2vc2 其中： 1 'c1=50 mycI 2 AB作平面运动币c2=下4+c2A vc2=10+20=2lo myc2 2 C2 「0=0 p=m20+m210=2mla B 方向水平向右

例3、两均质杆OA和AB质量为m，长为l，铰接于A。图示位 置时，OA杆的角速度为，AB杆相对OA杆的角速度亦为。 求此瞬时系统的动量。 解：由刚体系统的动量公式 1 C1 2 C2 p m v m v      其中：  2 1 l vC    l l v l C 2 2 2 2     m l ml l p m 2 5 2 2    方向水平向右。 mvC1 mvC2 O A B C1 C2  r= C A C A v v v 2 2    AB作平面运动  

10.1动量与冲量 10.1.2冲量 作用力与作用时间的乘积称为常力的冲量。 冲量是矢量，方向与力的方向一致。冲量的单位为NS, 与动量的量纲相同。 •常力的冲量 i-F 变力的冲量一元冲量 dI=Fdt 而力F在作用时间内的冲量是矢量积分 I=fFdr

10.1 动量与冲量 10.1.2 冲量 作用力与作用时间的乘积称为常力的冲量。 冲量是矢量，方向与力的方向一致。冲量的单位为N•s， 与动量的量纲相同。 •常力的冲量 I  Ft   •变力的冲量－元冲量 d I  F d t   而力F 在作用时间 内的冲量是矢量积分  t 0 d t  t  I F  

10.2动量定理 10.2.1质点的动量定理 d d ma m- （m)=F 'dt dt d(mv)=Fdt=dI 微分形式 质点动量的增量等于作用于质点上的力的元冲量。 mw-m,=∫Fdt=i 积分形式 在某一时间间隔内，质点动量的变化等于作用于质 点的力在此段时间内的冲量

10.2.1 质点的动量定理 质点动量的增量等于作用于质点上的力的元冲量。 d(mv)  F d t  d I    微分形式 10.2 动量定理 在某一时间间隔内，质点动量的变化等于作用于质 点的力在此段时间内的冲量。 0 0 d t m  m  t   v v F I     积分形式 d d ( ) d d m m m t t    v a v F    