《固体物理学》课程教学课件（PPT讲稿）Chapter 2 Wave Diffraction & the Reciprocal Lattice（2.1-2.5）

Ch2:Wave Diffraction the Reciprocal Lattice Objectives At the end of this Chapter,you should: 1. Understand the concept of the reciprocal lattice. 2.Know how to use the Bragg's law. 3.Know the relationship between Bragg's law and the Laue equation. 4. Know the drawing method and the concept of Brilluoin Zone. 5. Be able to calculate the structure factor of the typical crystal structures

At the end of this Chapter, you should: 1. Understand the concept of the reciprocal lattice. 2. Know how to use the Bragg’s law. 3. Know the relationship between Bragg’s law and the Laue equation. 4. Know the drawing method and the concept of Brilluoin Zone. 5. Be able to calculate the structure factor of the typical crystal structures Ch2：Wave Diffraction & the Reciprocal Lattice Objectives

2.1 The reciprocal lattice (direct)lattice reciprocal lattice primitive vectors a1,a2,a3 primitive vectors b1,b2,b3 Def. 1 6 -2 a b2=2n(a) b1∝a2×a3 because of orthogonality, then useb1·a1=2π 63-2 1 to determine the constant. Def. 2 b1·a1=2n,b1·a2=b1·a3=0, b2·a2=2n,b2·a3=b2·a1=0, b3·a3=2n,b3·a1=b3·a2=0

2.1

Reciprocal Lattice for Aluminium

Reciprocal Lattice for Aluminium

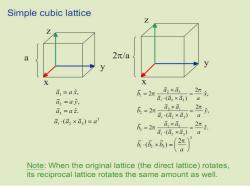
Simple cubic lattice Z a 2π/a y X a1=a元， 万=2π a2×a3 2元， a a,=ay, a1(a2×a) a3=a2 万=2π a3×a 2, a·(a2×a) a1(a2×a)=a3 万3=2π a1×a 2r. a1(a2×a3) 万(6×五)= Note:When the original lattice (the direct lattice)rotates, its reciprocal lattice rotates the same amount as well

FCC lattice BCC lattice Z An/a a X 6+》 6=2π ā×ā，-4机(+-2) a(a2×a)a2 a×a= 4π1 a+到 ，=2 a1(a2×a) 。2++) 日9 6=2π- axa a(a2×a3)=a3/4 低-)》

The reciprocal of a reciprocal lattice is the direct lattice: 6=2π a×a a(a2×a) C= 6,=2r a3×a, 低×动 a(a2×a) A×(BxC)=B(AC)-C(AB) i3=2 a×a a(a2×a) b:xb-m(asxa)x (axa)-aa 2π a1 21 2.2=i1(i2×i3)-2=(2π)2(a1b1)=(2π)3 Direct lattice Reciprocal lattice ， C1= 2xQY a-a cubic(a) 22 cubic(2π/a) fcc(a) bcc(4m/a) C2=a2,C3=a3, bcc(a) fcc(4元la) hexagonal (a,c) hexagonal(4π/N3a,2π/c) Take the reciprocal lattice as and rotated by 30 degrees direct one,start construct the reciprocal one:

The reciprocal of a reciprocal lattice is the direct lattice： 2 3 1 * 2 c b b ( )  =   2 2 3 3 1 1 2 1 2 2 (2 ) b b a a a a a ( ) ( )     =    =    A B C B A C C A B   = − ( ) ( ) ( ) * 2 3   =   = = b b b a b 1 2 3 1 1 ( ) (2 ) ( ) (2 )   2 1 1 1 * 2 (2 ) c a a   = =   c a c a 2 2 3 3 = = , , Take the reciprocal lattice as direct one, start construct the reciprocal one：

Two simple properties: R=n,a+n,a2+n,a3(n,h,n3∈Z)∈direct attice G=k+(k,k2,kZ)Ereciprocal lattice →G.R=2π(nk+n,k2+nk3)=2r×int eger. .exp(iG.R)is always equal to 1 Conversely,assume G.R=2rxinteger for all R, G.a =2nh, G.d=2nk, G.d=2nl, (h,k,l∈Z) then G=hd+k五，+瓜，（∈G)

If f(r)has lattice translation symmetry,that is,f(r)=f(r+R)for any lattice vector R [eg.f(r)can be the charge distribution in lattice], then it can be expanded as,f() all G where G is the reciprocal lattice vector. Pf Fourier expanson, f()=∑ef) f+=∑eef=f. R=h6+k6,+6 Yh,k,1 Therefore,e-1 for元 Fourier decomposition and reciprocal lattice vectors The expansion above is very general,it applies to all types of periodic lattice (e.g.bec,fec,tetragonal,orthorombic.) in all dimensions(1,2,and 3) All you need to do is to find out the reciprocal lattice vectors G

Two basic 1.(h,k,l)planes LG+b+ properties: 2.The distance between adjacent(h,k,1)planes, (useful later） d= 2 G See Prob.1 CA=04-0C= a1_a3 hh3 9 CB=OB-OC=92_a3 h hs Gh Ghthehy CA= a h+ha+Abn爱爱 h =2π-2π=0 图1-18晶面与倒易点阵位矢关系示意图 Ghibh,CB=0

1 3 1 3 2 3 2 3 a a CA OA OC h h a a CB OB OC h h = − = − = − = − 1 2 3 1 3 1 2 3 1 2 3 1 3 ( ) ( ) 2 2 0 G CA h h h a a h b h b h b h h   = + + − =−= G CB h h h 1 2 3 = 0

Geometrical relation between Ghk and(hkl)planes (Prob.1) (hkl)lattice planes G=2元n(n∈Z) → GR=2元n/小Gw .inter-plane distance dG For a cubic lattice G=h6+k5+, 2r(+k+) := a V2+k2+12 In general,planes with higher index have smaller inter-plane distance