《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.5 Heat capacity of the lattice

4.5 Heat capacity of the lattice 6E Cy Dugong-Petit law,numerical value aT =3R independent of T Classical Statistical no numerical value at finite T Mechanics >k. For a vibrating atom: E=K+U .N =m+号mv2+m+号k,x2+k,y2+号k.z2 Classical statistical mechanics-equipartition theorem:in thermal equilibrium each quadratic term in the E has an average energy 5kg7,s0:E,=6kT)=3k7 Classically for a vibrator Cy
4.5 Heat capacity of the lattice Classical Statistical Mechanics Dugong-Petit law, numerical value independent of T no numerical value at finite T Classically for a vibrator 2 2 2 1 2 2 1 2 2 1 2 2 1 2 2 1 2 1 1 mv mv mv k x k y k z E K U = x + y + z + x + y + z m = + ky kx kz For a vibrating atom: Classical statistical mechanics — equipartition theorem: in thermal equilibrium each quadratic term in the E has an average energy , so: k T 2 B 1 E 6( kB T) 3kB T 2 1 1 = =

for a crystal with N cells E=3NkT d E =3R≈25 dT mol K n The equipartition theorem Comparison of the Dulong-Petit law with experiment 77K(UK1) 273K(JK1) classical value 24.9 24.9 copper 12.5 24.3 aluminium 9.1 23.8 gold 19.1 25.2 lead 23.6 26.7 iron 8.1 24.8 sodium 20.4 27.6 silicon 5.8 21.8 2
Comparison of the Dulong-Petit law with experiment 77 K (JK-1 ) 273 K (JK-1 ) classical value 24.9 24.9 copper 12.5 24.3 aluminium 9.1 23.8 gold 19.1 25.2 lead 23.6 26.7 iron 8.1 24.8 sodium 20.4 27.6 silicon 5.8 21.8 2 for a crystal with N cells The equipartition theorem mol K J V V R n E dT d C = 3 25 =

The vibration mode with frequency of is composed of subsystems 1 E,=(n,+ho, ThepmhabitoisuoyseanthegentmsaeorE-ah -n ho/kgT e P n ho/kgT P=e-eo)∑=-x Theavcrmgeprohabilit T'heaverngeenenyTor thivihrntionmoie E=∑PE ho e (eho,kar-1) the relation between lattice vibration frequency and temperature
The vibration mode with frequency of j is composed of subsystems The probability of subsystem in the quantum state of The average probability The average energy for this vibration mode / 1 ( ) 2 1 j B j E Tj j k T e = + − the relation between lattice vibration frequency and temperature / 2 / 2 ( ) ( 1) j B j B k T j V B k T B e C k k T e = −

oj/kgT C,=k, e o,k-1) (e kgT >>ho ha, =1+ hightemperature ho Cy= Cr≈kB Dugong-Petit law 00088 kgT1 T→0 Cv→0 consistent with the experimental results
/ 2 / 2 ( ) ( 1) j B j B k T j V B k T B e C k k T e = − 2 2 2 (1 ) ( ) 1 [ ( ) ] 2 j j B V B B j j B B k T C k k T k T k T + + = + high temperature Dugong-Petit law 2 / 1 ( ) j B j V B k T B C k k T e = —— consistent with the experimental results low temperature

4.5.1 Einstein model ho e isuWehecrlcopeselofNatomsvibrnteswiththesnme freuenyog 3N E= ho Nha+ 3Nh@ Total energy )=2 ehab/kgT eha/kgT capacity Cy=( (e C,=3Nk/.K hoo/kgT e -Einstein heat e capacity function
3 ( ) 0 k T C Nk f B V B B = 4.5.1 Einstein model Assume the crystal composed of N atoms vibrates with the same frequency 0 / 1 ( ) 2 1 j B j E Tj j k T e = + − capacity Total energy / 2 / 0 0 2 ( 1) ( ) ( ) 0 0 − = k T k T B B B B B e e k T k T f -Einstein heat capacity function
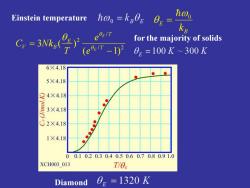
Einstein temperature h@o k2Og hoo eir g 0:=ka G,=3x,号 for the majority of solids (ee-12 0。=100K~300K 6×4.18 5×4.18 24×4.18 是3×418 G2×4.18 1×4.18 00.10.20.30.40.50.60.70.80.91.0 XCH003013 T/O Diamond 0E=1320K
Einstein temperature B E k 0 = / 2 / 2 ( 1) 3 ( ) − = T T E V B E E e e T C Nk for the majority of solids Diamond

hightcmperature ho1k9e=h0, 0>T kgT er1C=3,2 xperimental Cy=AT3
CV 3NkB B E 0 k = high temperature consistent with the experimental results low temperature k T B V B B e k T C Nk 0 0 2 3 ( ) − = B E 0 k = Experimental

Despite its success in reproducing the approach of Cy->0 as T >0,the Einstein model is clearly deficient at very low T.What might be wrong with the assumptions it makes? 3N independent oscillators,all with frequency o Discrete allowed energies: En=nhon=0,l,2,. ● At high T the small spacing between the energy levels is irrelevant. At sufficiently low temperature,the energy level separation is much bigger than kBT. Eventually all the oscillators are "frozen"in the ground state.Increasing T a little does not change this,i.e.it does not change the energy
• At high T the small spacing between the energy levels is irrelevant. • At sufficiently low temperature, the energy level separation is much bigger than kBT. • Eventually all the oscillators are “frozen” in the ground state. Increasing T a little does not change this, i.e. it does not change the energy. Despite its success in reproducing the approach of CV → 0 as T → 0, the Einstein model is clearly deficient at very low T. What might be wrong with the assumptions it makes? • 3N independent oscillators, all with frequency • Discrete allowed energies: E = n n = 0,1, 2, . n

Debye developed a more sophisticated treatment of atomic vibrations in solids Debye's model of a solid: 3N normal modes (patterns)of oscillations 。 Spectrum of frequencies from=0tomax Treat solid as continuous elastic medium (ignore details of atomic structure) 1)3 independent polarizations(L,T1,T2)with equal propagation speeds 2)continuous,elastic solid:=vk 3)x given by the value that gives the correct number of modes per polarization (N) This changes the expression for Cy because each mode of oscillation contributes a frequency-dependent heat capacity and we now have to integrate over all o:
Debye developed a more sophisticated treatment of atomic vibrations in solids. Debye’s model of a solid: • 3N normal modes (patterns) of oscillations • Spectrum of frequencies from = 0 to max • Treat solid as continuous elastic medium (ignore details of atomic structure) This changes the expression for CV because each mode of oscillation contributes a frequency-dependent heat capacity and we now have to integrate over all : 1) 3 independent polarizations (L, T1 , T2 ) with equal propagation speeds 2) continuous, elastic solid: = vgk 3) max given by the value that gives the correct number of modes per polarization (N)

4.5.2 Debye model 1912,Debye propose a model of continuous elastic media wave for the vibration waves @=Cq For Lognitudinal Wave Dispersion relation @=Cq For Transverse Wave For 3d crystal,the DoS (2n) V:the volume XCH003014 qy dq da da,dq the values of g are separated and distributed uniformly dq da,dq,dq. 9→q+dg (2π) The number of states (2π)月 4网dg
4.5.2 Debye model 1912, Debye propose a model of continuous elastic media wave for the vibration waves l t C q For Lognitudinal Wave C q For TransverseWave = = Dispersion relation For 3d crystal , the DoS V: the volume q dq V 2 3 4 (2 ) The number of states the values of q are separated , and distributed uniformly
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.1 Normal Modes of Vibration 4.2 Density of States 4.3 Harmonic approximation and normal mode coordinates 4.4 phonon.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3.1 General crystal binding 3.2 typical binding.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3(Supplement - Rules of crystal binding).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3.3 The cohesive energy for ionic crystal.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice(2.1-2.5).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice 2.6 X-Ray Diffraction Methods 2.7 Applications of XRD.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice(supplement - Review & Overview of X-Rays).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.9 Elements of Symmetry 1.10 Space groups 1.11 7 crystal system and 14 Bravis Lattice.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure(Supplement - microstructure and crystal system).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Introduction.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.1 Elementary Crystallography 1.2 Crystal Structure ≡ Lattice + Basis 1.3 Lattice Translation Vectors 1.4 Non-Bravais Lattices 1.5 Wigner-Seitz Method.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.6 typical crystal structure.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.7 Lattice Sites in a Cubic Unit Cell 1.8 crystal plane and miller index.ppt
- 《固体物理学》课程教学资源(参考资料)词汇汉英对照.pdf
- 《固体物理学》课程授课教案(讲义)第五章 能带理论.pdf
- 《固体物理学》课程授课教案(讲义)第一章 晶体结构.pdf
- 《固体物理学》课程授课教案(讲义)第三章 晶体的结合.pdf
- 《固体物理学》课程授课教案(讲义)第四章 晶格振动.pdf
- 《固体物理学》课程授课教案(讲义)第二章 晶体结构的测定.pdf
- 《固体物理学》课程授课教案(讲义)晶体能带结构理解电导特性.doc
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.1 general background and approximations 5.2 Bloch’s Theorem.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.6 Anharmonic Effects 4.7 Equation of states for Lattice 4.8 Experimental methods for the determinations of lattice vibration spectroscopy.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4(supplement - Thermal Expansion of Glass).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.5 The symmetry of bands.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.3 Nearly Free Electron 5.4 BZ and energy bands.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.4 Tight Binding Approximation(TBA).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 6 Electron motion in the crystal 6.1 The quasi-classical description of Bloch electrons 6.2. Electron quasi-momentum 6.3 The accelerated velocity and effective mass.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 6 Electron motion in the crystal 6(supplement - a more concise description of quasi-momentum).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 6 Electron motion in the crystal 6.4 The electron motion in a constant electric field 6.5 Band structure of conductor, insulator and semiconductor.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 7 The electronic theory of metal(supplement - Sommerfield expansion).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 7 The electronic theory of metal 7.1 Fermi statistics and the heat capacity of electron 7.2 Work function and contact potential.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.6 Density of states(DOS)and Fermi surface 5.7 the electrons in the crystal 5.8 the experimental results for DOS.ppt
- 《近代物理实验》课程教学大纲.doc
- 《近代物理实验》课程教学资源(PPT课件讲稿,共五部分).ppt
- 《工程光学》课程教学大纲 Engineering Optics.doc
- 安徽大学:《工程光学》课程授课教案(讲义,共十三章,授课教师:李桂华).doc
- 《工程光学》课程实验指导书(共六个实验).doc
- 《量子力学》课程教学课件(讲稿)Chapter 4 态和力学量的表象 The representation for the states and dynamical variable.pdf
- 《量子力学》课程教学课件(讲稿)Chapter 1 绪论 Quantum mechanism(量子力学的诞生).pdf
- 《量子力学》课程教学课件(讲稿)Chapter 2 波函数和薛定谔方程 The wave function and Schrödinger Equation.pdf
