《固体物理学》课程教学课件（PPT讲稿）Chapter 3 Interatomic Bonding 3.1 General crystal binding 3.2 typical binding

3.Interatomic Bonding Objectives At the end of this Chapter,you should: 1.Be able to identify the bonding type in the solids. 2.Be able to calculate the cohesive energy and the related physics parameters for ionic crystals and covalent crystals 3.Understand the concept of Madelung constant

3. Interatomic Bonding Objectives At the end of this Chapter, you should: 1.Be able to identify the bonding type in the solids. 2. Be able to calculate the cohesive energy and the related physics parameters for ionic crystals and covalent crystals 3. Understand the concept of Madelung constant

3.1 General crystal binding The stable bonding arrangement:the spatial configuration of positive ion cores outer electrons has a smaller QUANTUM MECHANICAL TOTAL ENERGY than any other configuration of these particles The Cohesive Energy:the energy difference of the configuration of atoms compared with that of the isolated atoms.~0.1 eV/atom for solids ~7 eV/atom or greater in some covalent some ionic compounds some metals. Each bonding mechanism between the atoms in a solid is a result of the electrostatic interaction between the nuclei the electrons

3.1 General crystal binding The stable bonding arrangement: the spatial configuration of positive ion cores & outer electrons has a smaller QUANTUM MECHANICAL TOTAL ENERGY than any other configuration of these particles The Cohesive Energy: the energy difference of the configuration of atoms compared with that of the isolated atoms. ~ 0.1 eV/atom for solids ~ 7 eV/atom or greater in some covalent & some ionic compounds & some metals. Each bonding mechanism between the atoms in a solid is a result of the electrostatic interaction between the nuclei & the electrons

The energy of a crystal is lower than that of the free atoms by an amount equal to the energy required to pull the crystal apart into a set of free atoms.This is called the crystal Binding (Cohesive)Enerqy. En=EN-U Uo:total energy when crystal is at OK,EN:the sum of energy for N free ionics.E(cohesive energy,binding energy):at OK, the energy needed to separate all the neutral free atoms from the crystal。Take EN=O, E6=-U

The energy of a crystal is lower than that of the free atoms by an amount equal to the energy required to pull the crystal apart into a set of free atoms. This is called the crystal Binding (Cohesive) Energy. E E U b N = − 0 E U b = − 0 U0 : total energy when crystal is at 0K，EN: the sum of energy for N free ionics. Eb (cohesive energy, binding energy) ：at 0K, the energy needed to separate all the neutral free atoms from the crystal。Take EN ＝0

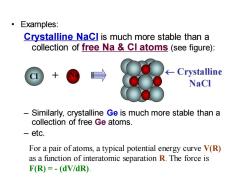
Examples: Crystalline Nacl is much more stable than a collection of free Na Cl atoms (see figure): Crystalline NaCl Similarly,crystalline Ge is much more stable than a collection of free Ge atoms. -etc. For a pair of atoms,a typical potential energy curve V(R) as a function of interatomic separation R.The force is F(R)=-(dV/dR)

• Examples: Crystalline NaCl is much more stable than a collection of free Na & Cl atoms (see figure): – Similarly, crystalline Ge is much more stable than a collection of free Ge atoms. – etc. Na  Crystalline NaCl Cl + For a pair of atoms, a typical potential energy curve V(R) as a function of interatomic separation R. The force is F(R) = - (dV/dR)

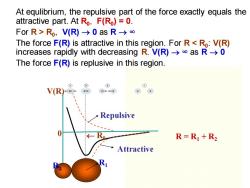
At equlibrium,the repulsive part of the force exactly equals the attractive part.At Ro,F(Ro)=0. ForR>Ro,V(R)-0asR→∞ The force F(R)is attractive in this region.For Ras R->0 The force F(R)is replusive in this region. V(R Repulsive 0 R=R1+R2 Attractive

R2 R1 V(R) 0  R0 Repulsive Attractive At equlibrium, the repulsive part of the force exactly equals the attractive part. At R0 , F(R0 ) = 0. For R > R0 , V(R) → 0 as R → ∞ The force F(R) is attractive in this region. For R < R0 : V(R) increases rapidly with decreasing R. V(R) → ∞ as R → 0 The force F(R) is replusive in this region. R = R1 + R2

Equations: u(r)= a,B.m.n>o determined by the experiment attractive repulsive 鞋≤ If stable: f(r)=- ou(r) =0 u(r) 8r2 >0 The equilibrium ou(r)=m- a b *0 nb m+1 -n- n-m Or 6=( ma The energy at ()=- (1-) m,≤习 stable point Another of-used expression (r）=- +Ae

If stable： 0 0 2 2 ( ) ( ) 0 ( ) 0 r r u r f r r u r r  = − =     The equilibrium 0 0 1 ( ) (1 ) m m u r r n The energy at = − − stable point 1 1 ( ) 0 m n u r a b m n r r r + +  = − =  1 0 ( )n m nb r ma − = Another of-used expression

Crystal cohesive energy If there are N atoms,the total energy will be: w之4器=÷】 2 r:the distance between the jth particle and the origin For cubic,take r:the nearest distance between two atoms b A- B= 2o Using equilibrium 6(A,B,m,n) condition

If there are N atoms，the total energy will be： 1 1 ij j j 1 j 1 j j 1 2 2 2 N N N m n N N a b U u u r r − − = =   = = = − +          i,j i≠j ( ) 2 j 0 j j m m n n N a b U r  r r   = − +        j j For cubic ，take r r = ， Crystal cohesive energy rj：the distance between the jth particle and the origin r: the nearest distance between two atoms 2 j 0 j m N a A  =  2 j 0 j n N b B  =  0 0 r dU dr     =   Using equilibrium condition ( ) ( ) 0 0 , , , , , , r A B m n U A B m n

Elastic properties for crystals: dp thermodynamically K= k(ar) P=-KA Ps aU a"U av K-Voav2 The first term is zero at equilibrium Classically understanding Exterior pressure Hook's law:Volumetric modulus S 6(A,B,m,n) U (A,B,m,n) K=Vo( a U Elastic modulus

Elastic properties for crystals： 1 ( )T P K V  V  = = −  thermodynamically V P K V  = − 0 0 2 2 V V U U U P V V V V         = − = − −            0 2 0 2 ( )V U K V V  =  dp K dV V =   −    The first term is zero at equilibrium Classically understanding Hook’s law: f dx K S x = V P K V  = − Exterior pressure Volumetric modulus 0 0 r dU dr     =   ( ) ( ) 0 0 , , , , , , r A B m n U A B m n 0 2 0 2 ( )V U K V V  =  Elastic modulus

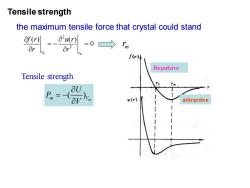
Tensile strength the maximum tensile force that crystal could stand f四=-aw =01m f(r) Repulsive Tensile strength aU Pm= av attractive

Tensile strength the maximum tensile force that crystal could stand ( ) m Vm U P V  = −  m r Repulsive attractive 2 2 ( ) ( ) 0 m m r r f r u r r r   = − =   m r Tensile strength

Basic types for crystals binding Attractive force:Coulomb interaction between opposite charges Repulsive force:Coulomb interaction between identical charges and Pauli exclusion law. Type of Form of Unit Solid Particles Forces Between Particles Properties Examples Molecular Atoms or London dispersion Fairly soft,low to moderately Argon,Ar;methane, molecules forces,dipole-dipole high melting point,poor CH4;sucrose, forces,hydrogen thermal and electrical C2H2O1:Dry bonds conduction IceTM,CO2 Covalent- Atoms connected Covalent bonds Very hard,very high melting Diamond,C;quartz, network in a network of point,often poor thermal SiO2 covalent bonds and electrical conduction Ionic Positive and Electrostatic Hard and brittle,high melting Typical salts-for negative ions attractions point,poor thermal and example,NaCl. electrical conduction Ca(NO3)2 Metallic Atoms Metallic bonds Soft to very hard,low to All metallic very high melting point, elements-for excellent thermal and example,Cu,Fe, electrical conduction, Al,Pt malleable and ductile In fact,bonding is complex and often composed of mixed

Basic types for crystals binding Attractive force: Coulomb interaction between opposite charges Repulsive force: Coulomb interaction between identical charges and Pauli exclusion law. In fact, bonding is complex and often composed of mixed