《量子力学》课程教学课件（讲稿）Chapter 4 态和力学量的表象 The representation for the states and dynamical variable

Chap.4 The representsllion for the stetes and dynamical varable Chapter.4 态和力学量的表象 The representation for the states and dynamical variable 按量子力学基本原理，体系的状态用波函数描述，力学量用线 性厄米算符表示。前面所使用的波函数及力学量算符是以坐标 这个力学量算符的本征值为变量写出它们的具体形式的。那么， 是否还可以选择其它力学量算符的本征值作为变量而写出波函 数及力学量算符的具体形式呢？回答是肯定的。这就是说量子 力学中波函数和力学量算符的描述方式不是唯一的，这正如几何 学中选用坐标系不是唯一的一样。坐标系有直角坐标系、球坐 标系、柱坐标系等，但它们对空间的描写是完全是等价的。 量子力学中态和力学量的具体表示方式称为表象

Chap.4 The representation for the states and dynamical variable 1 引 言 按量子力学基本原理,体系的状态用波函数描述,力学量用线 性厄米算符表示。前面所使用的波函数及力学量算符是以坐标 这个力学量算符的本征值为变量写出它们的具体形式的。那么, 是否还可以选择其它力学量算符的本征值作为变量而写出波函 数及力学量算符的具体形式呢？回答是肯定的。这就是说量子 力学中波函数和力学量算符的描述方式不是唯一的,这正如几何 学中选用坐标系不是唯一的一样。坐标系有直角坐标系、球坐 标系、柱坐标系等,但它们对空间的描写是完全是等价的。 量子力学中态和力学量的具体表示方式称为表象。 The representation for the states and dynamical variable The representation for the states and dynamical variable Chapter.4 态和力学量的表象

Chap.4 The representation for the states and dynamical varlable 4.1 态的表象 研究内容 The representation of the state 4.2 算符的矩阵表示 Matrix representation of operators 4.3 量子力学公式的矩阵表示 Matrix representation of formula for quantum mechanism 4.4幺正变换（可移至本章结尾） Unitary transformation 4.5 狄喇克符号 Dirac symbols 4.6 线形谐振子与占有数表象 Linear oscillator and occupation number representation 2

Chap.4 The representation for the states and dynamical variable 2 „ 4.1 态的表象 The representation of the state „ 4.2 算符的矩阵表示 Matrix representation of operators „ 4.3 量子力学公式的矩阵表示 Matrix representation of formula for quantum mechanism „ 4.4 幺正变换(可移至本章结尾) Unitary transformation „ 4.5 狄喇克符号 Dirac symbols „ 4.6 线形谐振子与占有数表象 Linear oscillator and occupation number representation 研 究 内 容

Chap.4 The representsllon for the states and dynamical varlable 一个定义： 表象的定义 重 态在任意表象中的表示； 二个表示： 点 算符在任意表象中的表示。 掌 平均值公式 ◆三个公式 本征值方程 在任意表象中 握 薛定谔方程 的表示 的 么正变换的基本性质 内容 狄喇克符号及应用 产生算符、湮灭算符、 粒子数算符及它 们的物理意义 主要数学工具： 矩阵 3

Chap.4 The representation for the states and dynamical variable 3 重 点 掌 握 的 内 容 ◆ 二个表示： 态在任意表象中的表示； 算符在任意表象中的表示。 ◆三个公式： 在任意表象中 的表示 平均值公式 本征值方程 薛定谔方程 ◆ 狄喇克符号及应用 ◆ 幺正变换的基本性质 ◆ 一个定义： 表象的定义 ◆ 产生算符、湮灭算符、粒子数算符及它 们的物理意义 主要数学工具: 矩阵

Chap.4 The representstion for the states and dynamical varlable §1态的表象 到目前为止，体系的状态都用坐标(x,y,)的函数表示，也 就是说描写状态的波函数是坐标的函数。力学量则用作用于坐标函 数的算符表示。但是这种描述方式在量子力学中并不是唯一的，这 正如几何学中选用坐标系不是唯一的一样。坐标系有直角坐标系、 球坐标系、柱坐标系等，但它们对空间的描写是完全是等价的。 波函数也可以选用其它变量的函数，力学量则相应的表示为作 用于这种函数上的算符。 表象：量子力学中态和力学量的具体表示方式称为表象。 以前采用的是坐标表象，下面我们要介绍其他表象。 (一)动量表象 (二)力学量表象 (三)讨论

Chap.4 The representation for the states and dynamical variable 4 （一）动量表象 （二）力学量表象 （三）讨论 §1 态的表象 到目前为止，体系的状态都用坐标(x,y,z)的函数表示，也 就是说描写状态的波函数是坐标的函数。力学量则用作用于坐标函 数的算符表示。但是这种描述方式在量子力学中并不是唯一的，这 正如几何学中选用坐标系不是唯一的一样。坐标系有直角坐标系、 球坐标系、柱坐标系等，但它们对空间的描写是完全是等价的。 波函数也可以选用其它变量的函数，力学量则相应的表示为作 用于这种函数上的算符。 表象：量子力学中态和力学量的具体表示方式称为表象。 以前采用的是坐标表象，下面我们要介绍其他表象

Chap.A The representslion for the stetes and dynamical varlable (一) 动量表象 在坐标表象中，体系的状态用波函数平（区，七）描写，这样一个态如 何用动量为变量的波函数描写在前面几章中已经有所介绍。 动量本征逐数 命题 假设平(x,t)是归一化波函 数，则C(p,t)也是归一。 Ψp(x)= ep1市 √2πh 证 组成完备系，任一 1=「Ψ*(x,t)平(x,t)d 状态Ψ可按其展开 展开系数 =∫刂C(p,w(x)p']*可C(p,)4(x)p1 平(x,)=了C(p,t)yn(x)p =∫∫C(p',)*C(p,)'∫y,*(x)w,x) C(p,t)=Jn*(x)Ψ(x,t) =∫∫C(p',)*C(p,t)p'dp6(p'-p) =∫C(p,)*C(p,t)p 5

Chap.4 The representation for the states and dynamical variable 5 在坐标表象中，体系的状态用波函数Ψ(x,t)描写，这样一个态如 何用动量为变量的波函数描写在前面几章中已经有所介绍。 动量本征函数： = = / 2 1 )( ipx p x e π ψ = 组成完备系，任一 状态Ψ可按其展开 ψ p )(),(),( dpxtpCtx ∫ =Ψ 展开系数 tpC = p Ψ ),()(*),( dxtxx ∫ ψ 假设 Ψ(x,t) 是归一化波函 数，则 C(p,t) 也是归一。 命题 证 Ψ= Ψ ),(),(*1 dxtxtx ∫ ψ p ψ p ])(),([*])(),([ dxdpxtpCpdxtpC ∫ ∫ ∫ = ′ ′ ′ dppdtpCtpC dxxx p p ),(*),( ′ ψψ )()(* ∫ ∫ ∫ = ′ ′ = ′ ′′ − ppdppdtpCtpC )(),(*),( ∫ ∫ δ ),(*),( dptpCtpC ∫ = （一）动量表象

Chap.4 The representstion for the states and dynamical varlable C(p,)的物理意义 1平c,2dx是在Ψc,)所描写的状态中，测量粒子的位 置所得结果在→x+dx范围内的几率。 C(①，)2dp是在Ψ(x,)所描写的状态中，测量粒子的动量所 得结果在p→p+dp范围内的几率。 平c,)与Cp,)一一对应，描述同一状态。ΨK,)是该状态在坐标表象 中的波函数；而C(P,)就是该状态在动量表象中的波函数。 若平(x,t)描写的态是具有确定 平(x,t)=yp(x)eiEA 动量p’的自由粒子态，即： 24

Chap.4 The representation for the states and dynamical variable 6 |C(p,t)| 2 d p 是在Ψ(x,t)所描写的状态中，测量粒子的动量所 得结果在 p → p + d p 范围内的几率。 |Ψ(x,t)| 2d x 是在Ψ(x,t)所描写的状态中，测量粒子的位 置所得结果在 x → x + d x 范围内的几率。 Ψ(x,t) 与 C(p,t) 一 一 对应,描述同一状态。Ψ(x,t)是该状态在坐标表象 中的波函数；而C(p,t) 就是该状态在动量表象中的波函数。 C(p,t)的物理意义 若Ψ(x,t) 描写的态是具有确定 动量 p’ 的自由粒子态，即： μ ψ 2 )(),( 2 / p E extx p tiE p p ′ = =Ψ ′ − ′ ′ =

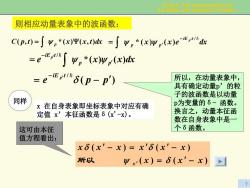
Chap.A The representsllon for the states and dynamical varlable 则相应动量表象中的波函数： C(p,)=∫9，*(x)平(x,t)=∫y。*(x)yn(x)ed在 =eem∫g,*(xwn(x) =e-i(p-p') 所以，在动量表象中， 具有确定动量p’的粒 子的波函数是以动量 同样 x在自身表象即坐标表象中对应有确 p为变量的6-函数。 定值x’本征函数是6(x-x)。 换言之，动量本征函 数在自身表象中是一 这可由本征 个6函数。 值方程看出： x6(x'-x)=x'6(x'-x) 所以 Ψx(x)=6(x'-x) 7

Chap.4 The representation for the states and dynamical variable 7 e dxxx p p p tiE )()(* / ′ − ∫ ′ = ψψ = )( / ppe p tiE = − ′ − ′ δ= 所以，在动量表象中， 具有确定动量p’的粒 子的波函数是以动量 p为变量的δ- 函数。 换言之，动量本征函 数在自身表象中是一 个δ函数。 x 在自身表象即坐标表象中对应有确 定值 x’本征函数是δ(x'-x)。 同样 这可由本征 值方程看出： )()( )()( xxx xxxxxx x = ′ − ′ − = ′ ′ − ψ ′ δ δ δ 所以 则相应动量表象中的波函数： tpC dxtxx p = Ψ ),()(*),( ∫ ψ dxexx tiE p p p / = )()(* − ′ = ∫ ψψ ′

Chap.4 The representstion for the states and dynamical varlable (二)力学量表象 推广上述讨论： x,p都是力学量，分别对应有坐标表象和动量表象， 因此可以对任何力学量Q都建立一种表象，称为力学量Q表象. 问题 那末，在任一力学量Q表象中，平(x,t)所描写的态又如何表示呢？ (1)具有分立本征值的情况 (2)含有连续本征值情况

Chap.4 The representation for the states and dynamical variable 8 那末,在任一力学量Q表象中,Ψ(x,t)所描写的态又如何表示呢？ 推广上述讨论： x, p 都是力学量，分别对应有坐标表象和动量表象， 因此可以对任何力学量Q都建立一种表象,称为力学量 Q 表象. 问题 （1）具有分立本征值的情况 （2）含有连续本征值情况 （二）力学量表象

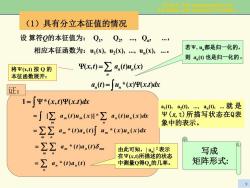
Chap.A The representstlon for the states and dynamical varlable (1)具有分立本征值的情况 设算符Q的本征值为：Q1,Q2,Q, 相应本征函数为：u1(),u2(),(, 若平，u都是归一化的， 0 则a)也是归一化的。 将平(k,)按Q的 x0=∑a.④u,y 本征函数展开： 证： a.0=∫4，*wxf) 1=∫平*(x,)Ψ(x.t)d a1(),a20,an(,.就是 =∫[∑an0un(x川*∑a,(0u,(x) Ψ(x,t)所描写状态在Q表 象中的表示。 =Σa.a.o”.*(xu.(e =22a.*0a,06 由此可知，|a2表示 写成 在Ψ(c,)所描述的状态 =2a.a.@ 中测量Q得Q的几率。 矩阵形式：

Chap.4 The representation for the states and dynamical variable 9 （1）具有分立本征值的情况 设 算符Q的本征值为： Q1, Q2, ., Qn, .， 相应本征函数为：u1(x), u2(x), ., un(x), .。 将Ψ(x,t) 按 Q 的 本征函数展开： ∫ ∑ Ψ= =Ψ dxtxxuta xutatx n n nn n ).()(*)( )()(),( 若Ψ, un都是归一化的， 则 an(t) 也是归一化的。 ∫ ΨΨ= ).(),(*1 dxtxtx 证： dxxutaxuta nn n m m m ∑ ∑ )()(*)]()([ ∫ = m n m n dxxuxutata m n )()(*)()(* ∑ ∑ ∫ = m n mn m n = ∑ ∑ tata )()(* δ tata )()(* n n n = ∑ 由此可知，| an| 2 表示 在Ψ(x,t)所描述的状态 中测量Q得Qn的几率。 a1(t), a2(t), ., an(t), . 就 是 Ψ(x,t)所描写状态在Q表 象中的表示。 写成 矩阵形式:

Chap.4 The representstion for the states and dynamical varlable 41(t) 共轭矩阵 a2(t) Ψ= 平=(4，)）*☑()*.n()*. a (t) 归一化可写为 a1(t) u2(t) 平+Ψ=(a,(t)* a2(t)*.an(t)* .) a (t) =∑a()*a.(0=1 10

Chap.4 The representation for the states and dynamical variable 10 ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ =Ψ ## )( )( )(21 ta ta tan 共轭矩阵 ( *)(*)( " *)( ") 1 2 =Ψ tata n ta + 归一化可写为 ( ) 1)(*)( )( )( )( *)(*)( *)( 2 1 1 2 = = ⎟⎟⎟⎟⎟⎟⎠⎞ ⎜⎜⎜⎜⎜⎜⎝⎛ =ΨΨ ∑ + tata ta ta ta tata ta n n n n n # " #