《量子力学》课程教学课件（讲稿）Chapter 3 量子力学中的力学量 The Dynamical variable in Quantum Mechanism

Chapt.3 The Dynamical variable in Quantum Mechanism 第三章量子力学中的力学量 The Dynamical variable in Quantum Mechanism 角动量、自旋、动能、势能、转动能等力学量以决定 论的方式描述。而量子力学的第一个惊人之举就是引入了 波函数，以概率的特征全面地描述了微观粒子的运动状 态。但波函数并不能作为量子力学中的力学量。于是， 又引入了一个重要的基本概念一一算符，用它表示量子力 学中的力学量。算符与波函数作为量子力学的核心概念相 辅相成、贯穿始终。 1

1 Chapt.3 The Dynamical variable in Quantum Mechanism 第三章 量子力学中的力学量 The Dynamical variable in Quantum Mechanism 角动量、自旋、动能、势能、转动能等力学量以决定 论的方式描述。而量子力学的第一个惊人之举就是引入了 波函数 ，以概率的特征全面地描述了微观粒子的运动状 态。但波函数 并不能作为量子力学中的力学量。于是， 又引入了一个重要的基本概念——算符，用它表示量子力 学中的力学量。算符与波函数作为量子力学的核心概念相 辅相成、贯穿始终

讲授内容 Chapt.3 The Dynamical variable in Quantum Mechanism 口3.1表示力学量的算符 operator for dynamical variable 口3.2动量算符与角动量算符 momentum operator and angular momentum operator 口3.3电子在库仑场中的运动 The motion of electrons in Coulomb field o3.4氢原子 Hydrogen atom 口3.5厄米算符本征函数的正交性 Orthonormality for eigenfunction of Hermitean operators 口3.6力学量算符与力学量的关系 Relationship between Operator and dynamical variable 口3☑算符的对易关系两力学量同时有确定值的条件测不准关系 Operator commute The Heisenberg Uncertainty Principle ▣3.8力学量随时间的变化守恒律 The dynamical variable with respect to time The conservation laws

2 Chapt.3 The Dynamical variable in Quantum Mechanism ‡3.1 表示力学量的算符 operator for dynamical variable ‡3.2 动量算符与角动量算符 momentum operator and angular momentum operator ‡3.3 电子在库仑场中的运动 The motion of electrons in Coulomb field ‡3.4 氢原子 Hydrogen atom ‡3.5 厄米算符本征函数的正交性 Orthonormality for eigenfunction of Hermitean operators ‡3.6 力学量算符与力学量的关系 Relationship between Operator and dynamical variable ‡3.7 算符的对易关系 两力学量同时有确定值的条件 测不准关系 Operator commute The Heisenberg Uncertainty Principle ‡3.8 力学量随时间的变化 守恒律 The dynamical variable with respect to time The conservation laws 讲授内容

学习内容 Chapt.3 The Dynamical variable in Quantum Mechanism 1.坐标算符、动量算符的表示形式及它们间的对易关系； 2. 角动量算符的表示形式及相关的对易关系； 3.动量算符本征函数的两种归一化：箱归二化和δ函数归 化： 4.角动量算符的共同本征函数及所对应的本征值； 5.正点电荷库仓场中电子运动的定态薛定谔方程及其求解的 基本步骤；定态波函数的表达形式：束缚态的能级及其简 并度：氢原子的能级、光谱线的规律；电子在核外的概率 分布；电离能和里德伯常数； 6.量子力学的力学量与厄米算符的关系；厄米算符的本征函 数组成正交完备集； 7.在什么情况下力学量具有确定值；力学量可能值、概率、 平均值的计算方法，两个力学量同时具有确定值的条件； 8.不确定关系及其应用； 9.守恒量的判断方法

3 Chapt.3 The Dynamical variable 学习内容 in Quantum Mechanism 1．坐标算符、动量算符的表示形式及它们间的对易关系； 2．角动量算符的表示形式及相关的对易关系； 3．动量算符本征函数的两种归一化：箱归一化和 函数归一 化； 4．角动量算符的共同本征函数及所对应的本征值； 5．正点电荷库仓场中电子运动的定态薛定谔方程及其求解的 基本步骤；定态波函数的表达形式；束缚态的能级及其简 并度；氢原子的能级、光谱线的规律；电子在核外的概率 分布；电离能和里德伯常数； 6．量子力学的力学量与厄米算符的关系；厄米算符的本征函 数组成正交完备集； 7．在什么情况下力学量具有确定值；力学量可能值、概率、 平均值的计算方法，两个力学量同时具有确定值的条件； 8．不确定关系及其应用； 9．守恒量的判断方法。 δ

重点掌握内容 Chapt.3 The Dynamical variable in Quantum Mechanism 一个基本概念：厄米算符（作用及其基本性质）； 两个假设：力学量用厄米算符表示； 状态用厄米算符本征态表示，力学量 算符的本征值为力学量的可测值 三个力学量计算值：确定值、可能值、平均值； 四个力学量算符的本征态及本征值：坐标算符，动量 算符，角动量算符及能量算符（哈密顿算 符)及它们的本征值。 一个关系：力学量算符间的对易关系（特别是坐标 算符与动量算符的对易关系，角动量算符 对易关系) 三个定理：共同本征态定理（包括逆定理） 不确定关系 力学量守恒定理

4 Chapt.3 The Dynamical variable 重点掌握内容 in Quantum Mechanism 一个基本概念：厄米算符（作用及其基本性质）； 两个假设： 力学量用厄米算符表示； 状态用厄米算符本征态表示，力学量 算符的本征值为力学量的可测值 三个力学量计算值：确定值、可能值、平均值； 四个力学量算符的本征态及本征值：坐标算符，动量 算符，角动量算符及能量算符（哈密顿算 符）及它们的本征值。 一个关系：力学量算符间的对易关系（特别是坐标 算符与动量算符的对易关系，角动量算符 对易关系） 三个定理: 共同本征态定理（包括逆定理） 不确定关系 力学量守恒定理

3.1表示力学量的算符 Chap.3 The Dynamical variable in Quantum Mechanism 1.坐标与动量的平均值及坐标算符与动量算符的引入 由前面的讨论，我们看到，当微观粒子处在某 一状态时，一般而言，其力学量（如坐标、动量和 能量等)不一定具有确定的值，而以一定几率分布 取一系列可能值（当然，可能在某些特殊的状态， 有些力学可取确定值)。 若已知粒子在坐标表象中的状态波函数w(F,) 按照波函统计解释，利用统计平均方法，可求得粒 子坐标(x,y,z)或的平均值 若知道粒子在动量表象中的波函数C(p,t),同理 可求出粒子动量(P,P,P)或P的平均值。 5

5 Chap.3 The Dynamical variable in Quantum Mechanism 由前面的讨论，我们看到，当微观粒子处在某 一状态时，一般而言，其力学量（如坐标、动量和 能量等）不一定具有确定的值，而以一定几率分布 取一系列可能值（当然，可能在某些特殊的状态， 有些力学可取确定值）。 若知道粒子在动量表象中的波函数 ，同理 可求出粒子动量 或 的平均值。 tpC ),( K P K (, ,) PPP x y 若已知粒子在坐标表象中的状态波函数 ， 按照波函统计解释，利用统计平均方法，可求得粒 子坐标 或 的平均值 tr ),( 3.1 表示力学量的算符 1.坐标与动量的平均值及坐标算符与动量算符的引入 K ψ zyx ),( r G

3.1表示力学量的算符（续1） Chapt.3 The Dynamical variable in Quantum Mechanism (1)坐标平均值 设粒子的状态波函数为w(俨，t)或C(P,t) ur0 jc”dn 水 粒子的位置处在：x~x+,y~y+少，z~z+化间的几率为 @(r,t)d-w(r,t)'d'r 坐标平均值 =∫Foa,d行=jw(G,ry,f行

6 Chapt.3 The Dynamical variable in Quantum Mechanism （1）坐标平均值 3 3/2 1 (,) ( ,) (2 ) i P r ψ r t CPte dP π ∞ ⋅ −∞ = ∫∫∫ K K = K K K = 设粒子的状态波函数为 或tr ),( K ψ tPC ),( K 3 3/2 1 ( ,) (,) (2 ) i P r CPt ψ rte dr π ∞ − ⋅ −∞ = ∫∫∫ K K = K K K = rdtrrdtrK 3 K K 2 3 K ω = ψ ),(),( 粒子的位置处在： x ~ ,~ ,~ x dx y y dy z z dz + + + 间的几率为 3.1 表示力学量的算符（续1） ∫∫ ∞ ∞− ∞ ∞− >=< = rdtrrtrrdtrrr 3 * 3KKKKKKKK 坐标平均值 ω ψψ ),(),(),(

3.1表示力学量的算符（续2） Chapt.3 The Dynamical variable in Quantum Mechanism 利用C(P,)计算出坐标产的平均值： =j∬C(p,C(P,)dF -00 称为坐标算符 Prove: <>w'(F,t)Fw(F,t)d 2Jwc,cP,e”ip 2rJircPy,ere 对此作一次分部积分

7 Chapt.3 The Dynamical variable in Quantum Mechanism 利用 计算出坐标 的平均值: tPC ),( K r K PdtPCrtPCr K K K K K * 3 ),( ˆ ),( ∫∫∫ ∞− >==< ψψ * 3 3 3 /2 ( 1 (,)[ ( , 2 ) ) ] i P r ψ rtr CPte dP d r π ′⋅ = ′ ′ ∫ ∫ K K = K K = K K K 3.1 表示力学量的算符（续2） 对此作一次分部积分 * 3 3 3/2 1 ( , )[ ( , ) ] (2 ) i P r P rt CPt e dP dr i ψ π ′⋅ ′ = ∇ ′ ′ ∫ ∫ K K = K = K K K =

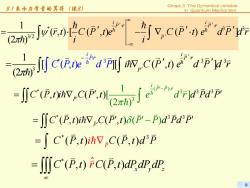
31表示力学量的算将（续3） Chapt.3 The Dynamical variable in Quantum Mechanism e的we 2Ceea.c动up -∬cBao,aj。r"PWr4D -[C(P.t)ihV C(P,t)8(P-P)dPdP =」C(P,)ihvC(p,t)dp =Jjc(p,)C(P,t)dP.d那，adr

8 Chapt.3 The Dynamical variable in Quantum Mechanism * 3 3 3 3 1 [ ][ ( , ) ( ) , ) ] 2 ( i i P P r P r C Pt e d P i CP t e dP dr π ′⋅ ′ − ⋅ = ∇ ′ ′ ∫ ∫ ∫ K K = K K K = K K K = K K = ( ) * 3 3 3 3 1 [ ] (2 ) ( ,) ( ,) i P P P r C Pti CP t e dr d Pd P π ′− ′ ⋅ = ∇ ′ ′ ∫∫ ∫ K K K = K K K K = K K = * 3 3 ( ,) ( , ) ( ) C Pti CP t dP P = ∇ ′ ′ δ P′− P d P ′ ∫∫ K K K K K K K = * 3 ( ,) ( ,) C Pt CPtdP P = i ∇ ∫ K K K = K *( ,) ( ,) ˆ C P t C P t dP dP dP x y z r ∞ = ∫∫∫ K K K 3.1 表示力学量的算符（续3） * 3 3 3/2 1 (,)[ ( ,) ( ) ] (2 ) i i P r P r P rt C P te C P t e dP dr i i ψ π ∞ ′ ′ ⋅ ⋅ ′ −∞ = ⋅ −∇ ⋅ ′ ′′ ∫ ∫ K K K K = = K = = K KK K K =

Chapt.3 The Dynamical variable 3.1表示力学量的算符（续4） in Quantum Mechanism 其中 产=权。=诚 坐标算符 (2)动量平均值 粒子的动量值处于P~P+迟，PP+心，P~卫+P 间的几率为： @(P.t)dP=C(P,t)dP 动量平均值=jy(,0P,)a时 9

9 Chapt.3 The Dynamical variable in Quantum Mechanism （2）动量平均值 粒子的动量值处于 Px ~ ,~ ,~ P dP P P dP P P dP x xy y yz z z + + + 间的几率为: PdtPCPdtP K K K K 3 2 3 ω = ),(),( 利用坐标为变量的波函数 计算动量平均值: tr ),(K ψ 其中 ˆ P ─ 坐标算符 xy z ri i i j k pp p ⎛ ⎞ ∂∂∂ = ∇= + + ⎜ ⎟ ⎜ ⎟ ∂∂∂ ⎝ ⎠ G G G G G = = P rdtrPtr K K K K K * 3 ),( ˆ ),( ψψ ∫∫∫ ∞ >==< = PdtPCPtPCPdtPCPP K K K K K K K K 3 * 3 2 动量平均值 ),( ),(),(

3.1表示力学量的算符（续5） Chapt.3 The Dynamical variable in Quantum Mechanism 分=-V 一动量算符 Prove:=C(P,)PC(P,t)dp -Scuamfvw 2fc2训c.omed7p Beur-jmrtarr efo加dr1-fw." 10

10 Chapt.3 The Dynamical variable in Quantum Mechanism Prove: PdtPCPtPCPK K K K K * 3 ),(),( ∫∫∫ >=< 3 3/2 * 3 1 [ (,) ] (2 ( ,) ) i P r C PtP ψ r t e dr d P π − ⋅ = ∫ ∫ K K = K K = K K K * 3 3 3 / 2 1 ( , )[ (,) ] (2 ) i P r C Pt r t i e dr d P π ψ − ⋅ = ∇ ∫ ∫ K K = K K = K K = * 3/ 3 3 2 1 ( , )[ (,) ( (,) ) ) ] (2 i i P r P r C Pt ψ ψ rtie i rt e dr d P π ∞ − ⋅ − ⋅ −∞ = − ∇ ∫ ∫ K K K K = = K KK K = = K = =∇−= ─ 动量算符 K iPˆ 3 1 * 3 3 3 [ ( ,) ] (2 ) [ ( ( , )) ] i P i P r r ψ r te d r i rt ψ e d r d P π ⎧ ⎫ ⋅ ′ − ⋅ = ⎨ ⎬ ′ ′ ⎩ ⎭ − ∇ ∫ ∫ ∫ K K = K K = K K K = K K = 3.1 表示力学量的算符（续5）