《大学物理学》课程作业习题（含解答）第5章作业题

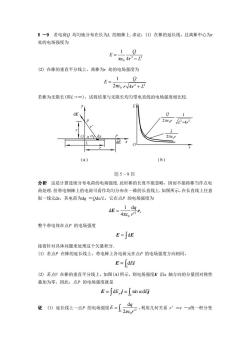
5一9若电荷Q均匀地分布在长为L的细棒上.求证：（1）在棒的延长线，且离棒中心为处的电场强度为EQ元4r-L(2）在棒的垂直平分线上，离棒为r处的电场强度为F:2元80r/4r2+L?若棒为无限长（即L→），试将结果与无限长均匀带电直线的电场强度相比较QE2m802+4r2(b)(a)题5-9图分析这是计算连续分布电荷的电场强度.此时棒的长度不能忽略，因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示，在长直线上任意取一线元dx，其电荷为dq=Qdx/L，它在点P的电场强度为IgedE=4元c0r整个带电体在点P的电场强度E=JdE接着针对具体问题来处理这个失量积分。（1）若点P在棒的延长线上，带电棒上各电荷元在点P的电场强度方向相同，E= JdEi(2）若点P在棒的垂直平分线上，如图(A)所示，则电场强度E沿x轴方向的分量因对称性叠加为零，因此，点P的电场强度就是E=J dE,j=I sin αdEj证（1）延长线上一点P的电场强度E=，利用几何关系=F—x统一积分变12元2or

5 －9 若电荷Q 均匀地分布在长为L 的细棒上.求证：(1) 在棒的延长线，且离棒中心为r 处的电场强度为 2 2 π 0 4 1 r L Q ε E − = (2) 在棒的垂直平分线上，离棒为r 处的电场强度为 2 2 2π 0 4 1 r r L Q ε E + = 若棒为无限长(即L→∞)，试将结果与无限长均匀带电直线的电场强度相比较. 分析 这是计算连续分布电荷的电场强度.此时棒的长度不能忽略，因而不能将棒当作点电 荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示，在长直线上任意 取一线元dx，其电荷为dq ＝Qdx/L，它在点P 的电场强度为 r r q ε E e 2 0 d 4π 1 d  = 整个带电体在点P 的电场强度  E = dE 接着针对具体问题来处理这个矢量积分. (1) 若点P 在棒的延长线上，带电棒上各电荷元在点P 的电场强度方向相同，  = L E dEi (2) 若点P 在棒的垂直平分线上，如图(A)所示，则电场强度E 沿x 轴方向的分量因对称性 叠加为零，因此，点P 的电场强度就是   = = L E dEy j sin αdEj 证 (1) 延长线上一点P 的电场强度   = L πε r q E 2 2 0 d ，利用几何关系 r′＝r －x统一积分变

量，则odxQ电场强度的方向E, 5 40, 705 40,[,-L/2 + /2] 0 4-7沿x轴(2）根据以上分析，中垂线上一点P的电场强度E的方向沿y轴，大小为E-1 magae利用几何关系sinα=r/r，r=P+x统一积分变量，则rOd0E-In e+3=2元eor/4r2+当棒长L→时，若棒单位长度所带电荷入为常量，则P点电场强度O/LE= lim 2meor /1+4rIr=2元00r此结果与无限长带电直线周围的电场强度分布相同［图(B)］.这说明只要满足P/L2<<1,带电长直细棒可视为无限长带电直线5-10一半径为R的半球壳，均匀地带有电荷，电荷面密度为，求球心处电场强度的大小题5-10图分析这仍是一个连续带电体问题，求解的关键在于如何取电荷元.现将半球壳分割为一组平行的细圆环，如图所示，从教材第5－3节的例1可以看出，所有平行圆环在轴线上P处的电场强度方向都相同，将所有带电圆环的电场强度积分，即可求得球心0处的电场强度，解将半球壳分割为一组平行细圆环，任一个圆环所带电荷元dg=odS=8.2元R°sinQd0，在点0激发的电场强度为

量，则 ( ) 2 2 0 0 2 2 2 0 π 4 1 / 2 1 / 2 1 4π d 4π 1 r L Q ε L r L r L ε Q L r x Q x ε E L/ -L/ P − =       + − − = − =  电场强度的方向 沿x 轴. (2) 根据以上分析，中垂线上一点P 的电场强度E 的方向沿y 轴，大小为 E ε r α q E L d 4π sin d 2 0   = 利用几何关系 sin α＝r/r′， 2 2 r  = r + x 统一积分变量，则 ( ) 2 2 0 2 / 3 2 2 2 2 0 4 1 2π d 4π 1 ε r r L Q L x r rQ x ε E L/ -L/ + = + =  当棒长L→∞时，若棒单位长度所带电荷λ为常量，则P 点电场强度 ε r λ r L Q L ε r E l 0 2 2 0 2π 1 4 / / 2π 1 lim = + = → 此结果与无限长带电直线周围的电场强度分布相同［图(B)］.这说明只要满足r 2/L 2 ＜＜1， 带电长直细棒可视为无限长带电直线. 5 －10 一半径为R 的半球壳，均匀地带有电荷，电荷面密度为σ，求球心处电场强度的大 小. 分析 这仍是一个连续带电体问题，求解的关键在于如何取电荷元.现将半球壳分割为一组 平行的细圆环，如图所示，从教材第5 －3 节的例1 可以看出，所有平行圆环在轴线上P 处 的电场强度方向都相同，将所有带电圆环的电场强度积分，即可求得球心O 处的电场强度. 解 将半球壳分割为一组平行细圆环，任一个圆环所带电荷元 dq δdS δ 2πR sin θ dθ 2 = =  ，在点O 激发的电场强度为

xdqdE:4ne (P+rppsi由于平行细圆环在点O激发的电场强度方向相同，利用几何关系x=RcosO，r=RsinQ统一积分变量，有xdq Recos?g.2aR'sn 0dedE -40(+r134元0R3sinOcosde积分得E-I"2 sin osa -485一12两条无限长平行直导线相距为ro，均匀带有等量异号电荷，电荷线密度为入（1）求两导线构成的平面上任一点的电场强度（设该点到其中一线的垂直距离为x)：(2）求每一根导线上单位长度导线受到另一根导线上电荷作用的电场力。S题5-12图分析（1）在两导线构成的平面上任一点的电场强度为两导线单独在此所激发的电场的叠加。（2）由F=qE，单位长度导线所受的电场力等于另一根导线在该导线处的电场强度乘以单位长度导线所带电量，即：F=IE.应该注意：式中的电场强度E是另一根带电导线激发的电场强度，电荷自身建立的电场不会对自身电荷产生作用力。解（1）设点P在导线构成的平面上，E+、E-分别表示正、负带电导线在P点的电场强度，则有

( ) E i 2 / 3 2 2 0 d 4π 1 d x r x q ε + = 由于平行细圆环在点O 激发的电场强度方向相同，利用几何关系 x = Rcosθ ，r = Rsin θ 统 一积分变量，有 ( ) θ θ θ ε δ δ πR θ θ R R θ x r πε x q πε E sin cos d 2 2 sin d cos 4 d 1 4 1 d 0 2 3 0 2 / 3 2 2 0 = =  + = 积分得 0 / 2 0 0 4 sin cos d 2 ε δ θ θ θ ε δ E π  = = 5 －12 两条无限长平行直导线相距为r0 ，均匀带有等量异号电荷，电荷线密度为λ.(1) 求 两导线构成的平面上任一点的电场强度( 设该点到其中一线的垂直距离为x)；(2) 求每一根 导线上单位长度导线受到另一根导线上电荷作用的电场力. 分析 (1) 在两导线构成的平面上任一点的电场强度为两导线单独在此所激发的电场的叠 加.(2) 由F ＝qE，单位长度导线所受的电场力等于另一根导线在该导线处的电场强度乘以 单位长度导线所带电量，即：F ＝λE.应该注意：式中的电场强度E 是另一根带电导线激发 的电场强度，电荷自身建立的电场不会对自身电荷产生作用力. 解 (1) 设点P 在导线构成的平面上，E＋、E－分别表示正、负带电导线在P 点的电场强度， 则有

E-E.+E,-2元80x-x2元x-x)(2）设F+、F-分别表示正、负带电导线单位长度所受的电场力，则有F=E. =2元e1F, =-AE, =-2元2g0显然有F+=F-，相互作用力大小相等，方向相反，两导线相互吸引5一15边长为a的立方体如图所示，其表面分别平行于OxyOy和Ozx平面，立方体的个项点为坐标原点.现将立方体置于电场强度E=(E,+kx)i+E,j(k,Ei，E2为常数)的非均匀电场中，求电场对立方体各表面及整个立方体表面的电场强度通量。题5-15图解如图所示，由题意E与Oxy面平行，所以任何相对Oxy面平行的立方体表面，电场强度的通量为零，即PoABC=@DEFG=0.而@ABGP=E·dS-[(E, +kx)i+E,](dsi)= E,a?考虑到面CDEO与面ABGF的外法线方向相反，且该两面的电场分布相同，故有@CDEO =-@ABGF =-E,d同理@AOEr =J E·dS = [(E;i+ E,j)] (-dsi)=-E,aDBcDG =[E - dS = [[(E, + ka)i+ E,]]- (dsi)=(E, + ka)a?因此，整个立方体表面的电场强度通量@=E@=kd

( ) i E E E i x r x r ε λ ε x r x λ − =         − = − + + = + 0 0 0 0 0 2π 1 1 2π (2) 设F＋、F－分别表示正、负带电导线单位长度所受的电场力，则有 F E i 2π 0 0 ε r λ + = λ − = F E i 0 0 2 2πε r λ − = −λ + = − 显然有F＋＝F－，相互作用力大小相等，方向相反，两导线相互吸引. 5 －15 边长为a 的立方体如图所示，其表面分别平行于Oxy、Oyz 和Ozx 平面，立方体的 一个顶点为坐标原点.现将立方体置于电场强度 E = i + j (E kx E 1 2 + ) (k，E1 ，E2 为常数) 的非均匀电场中，求电场对立方体各表面及整个立方体表面的电场强度通量. 解 如图所示，由题意E 与Oxy 面平行，所以任何相对Oxy 面平行的立方体表面，电场强 度的通量为零，即 ΦOABC = ΦDEFG = 0 .而 ( )  ( ) 2 ABGF =  d = E1 + k x + E2  dS = E2a   Φ E S i j j 考虑到面CDEO 与面ABGF 的外法线方向相反，且该两面的电场分布相同，故有 2 ΦCDEO = −ΦABGF = −E2a 同理 ( ) ( ) 2 AOEF =  d = E1 + E2  − dS = −E1a   Φ E S i j i ( )  ( ) ( ) 2 ΦBCDG =  d = E1 + k a + E2  dS = E1 + k a a   E S i j i 因此，整个立方体表面的电场强度通量 3 Φ = Φ = ka

5－17设在半径为R的球体内，其电荷为球对称分布，电荷体密度为p=kr (0≤r≤R)p=0(r>R)k为一常量.试分别用高斯定理和电场叠加原理求电场强度E与r的函数关系。(a)(b)题5-17图分析通常有两种处理方法：（1）利用高斯定理求球内外的电场分布.由题意知电荷呈球对称分布，因而电场分布也是球对称，选择与带电球体同心的球面为高斯面，在球面上电场强度大小为常量，且方向垂直于球面，因而有（E·dS=E.4元r根据高斯定理fE·ds=一[pdV，可解得电场强度的分布.(2）利用带电球壳电场叠加的方法求球内外的电场分布.将带电球分割成无数个同心带电球壳，球壳带电荷为dg=p·4元rdr，每个带电球壳在壳内激发的电场dE=0，而在球壳外激发的电场d-由电场叠加可解得带电球体内外的电场分布E(r)=’dE (0≤r≤R)E()=["'dE (r>R)解1因电荷分布和电场分布均为球对称，球面上各点电场强度的大小为常量，由高斯定理E·dS=-pdV得球体内（0≤<R)E(r)4mr2 -=,kr4r°dr

5 －17 设在半径为R 的球体内，其电荷为球对称分布，电荷体密度为 ( ) ρ (r R) ρ kr =  =   0 0 r R k为一常量.试分别用高斯定理和电场叠加原理求电场强度E与r的函数关系. 分析 通常有两种处理方法：(1) 利用高斯定理求球内外的电场分布.由题意知电荷呈球对 称分布，因而电场分布也是球对称，选择与带电球体同心的球面为高斯面，在球面上电场强 度大小为常量，且方向垂直于球面，因而有 2 S d = E4πr  E S 根据高斯定理    = ρ V ε d 1 d 0 E S ，可解得电场强度的分布. (2) 利用带电球壳电场叠加的方法求球内外的电场分布.将带电球分割成无数个同心带电球 壳，球壳带电荷为 dq = ρ  4πr  dr  2 ，每个带电球壳在壳内激发的电场 dE = 0 ，而在球壳 外激发的电场 r ε r q E e 2 4π 0 d d = 由电场叠加可解得带电球体内外的电场分布 ( ) ( ) (r) (r R) r R r =  =     d d 0 r R 0 0 E E E E 解1 因电荷分布和电场分布均为球对称，球面上各点电场强度的大小为常量，由高斯定理    = ρ V ε d 1 d 0 E S 得球体内(0≤r≤R) ( ) 4 0 0 2 0 2 π 4π d 1 4π r ε k kr r r ε E r r r = = 

krE()=460球体外(r>R)I["kr4元r°dr=元KE(r/4元r =E(c)= kR)460解2将带电球分割成球壳，球壳带电dq= pdV=kr'4元r"dr由上述分析，球体内(0≤R)R 1 kr" 4r"dr'kkE(r)= [R4元起5一18一无限大均匀带电薄平板，电荷面密度为g，在平板中部有一半径为r的小圆孔求圆孔中心轴线上与平板相距为x的一点P的电场强度，(b)(a)题5-18图分析用补偿法求解利用高斯定理求解电场强度只适用于几种非常特殊的对称性电场.本题的电场分布虽然不具有这样的对称性，但可以利用具有对称性的无限大带电平面和带电圆盘的电场叠加，求出电场的分布.若把小圆孔看作由等量的正、负电荷重叠而成，挖去圆孔的带电平板等效于一个完整的带电平板和一个带相反电荷（电荷面密度=一α)的小圆盘.这样中心轴线上的电场强度等效于平板和小圆盘各自独立在该处激发电场的矢量和。解由教材中第5一4节例4可知，在无限大带电平面附近

( ) r ε kr E r e 0 2 4 = 球体外(r ＞R) ( ) 4 0 0 2 0 2 π 4π d 1 4π r ε k k r r r ε E r r R = =  ( ) r ε kR E r e 0 2 4 = 解2 将带电球分割成球壳，球壳带电 dq = ρdV = kr 4πr  dr  2 由上述分析，球体内(0≤r≤R) ( ) r r r ε kr r kr r r ε E r e e 0 2 2 2 0 0 4 4π d 4π 1 =    =  球体外(r ＞R) ( ) r r R ε r k R r kr πr r πε E r e e 2 0 2 2 2 0 0 4 4 d 4 1 =    =  5 －18 一无限大均匀带电薄平板，电荷面密度为σ，在平板中部有一半径为r 的小圆孔. 求圆孔中心轴线上与平板相距为x 的一点P 的电场强度. 分析 用补偿法求解利用高斯定理求解电场强度只适用于几种非常特殊的对称性电场.本题 的电场分布虽然不具有这样的对称性，但可以利用具有对称性的无限大带电平面和带电圆盘 的电场叠加，求出电场的分布.若把小圆孔看作由等量的正、负电荷重叠而成，挖去圆孔的 带电平板等效于一个完整的带电平板和一个带相反电荷(电荷面密度σ′＝－σ)的小圆盘.这 样中心轴线上的电场强度等效于平板和小圆盘各自独立在该处激发电场的矢量和. 解 由教材中第5 －4 节例4 可知，在无限大带电平面附近

E,=2%ene,为沿平面外法线的单位矢量；圆盘激发的电场E,=-2(-2+F它们的合电场强度为E=E+E-2%*+r在圆孔中心处x=0，则E=0在距离圆孔较远时x>>r，则E=20V1+r:/x2°上述结果表明，在x>>r时，带电平板上小圆孔对电场分布的影响可以忽略不计5-21两个带有等量异号电荷的无限长同轴圆柱面，半径分别为R和R2>R1），单位长度上的电荷为入.求离轴线为r处的电场强度：（1）rR2(a)(b)题5-21图分析电荷分布在无限长同轴圆柱面上，电场强度也必定沿轴对称分布，取同轴圆柱面为高

n ε σ E e 0 1 2 = n e 为沿平面外法线的单位矢量；圆盘激发的电场 n x r x ε σ E e         + = − − 2 2 0 2 1 2 它们的合电场强度为 n x r x ε σ E E E e 2 2 0 1 2 2 + = + = 在圆孔中心处x ＝0，则 E ＝0 在距离圆孔较远时x ＞＞r，则 n n ε σ ε r x σ e E e 0 2 2 0 2 1 / 1 2  + = 上述结果表明，在x ＞＞r 时，带电平板上小圆孔对电场分布的影响可以忽略不计. 5 －21 两个带有等量异号电荷的无限长同轴圆柱面，半径分别为R1 和R2 ＞R1 )，单位长 度上的电荷为λ.求离轴线为r 处的电场强度：(1) r ＜R1 ，(2) R1 ＜r ＜R2 ，(3) r ＞ R2 . 分析 电荷分布在无限长同轴圆柱面上，电场强度也必定沿轴对称分布，取同轴圆柱面为高

斯面，只有侧面的电场强度通量不为零，且EdS=E·2元rL，求出不同半径高斯面内的申荷Zq.即可解得各区域电场的分布。解，作同轴圆柱面为高斯面，根据高斯定理E-2rL=Zq/80Zq=0rR2.Zq=0E, =0在带电面附近，电场强度大小不连续，电场强度有一跃变ALAE =2元02元80L这与5-20题分析讨论的结果一致5—22如图所示，有三个点电荷Q1、Q2、Q:沿一条直线等间距分布且Q1=0：=0.已知其中任一点电荷所受合力均为零，求在固定Q1Q：的情况下，将Q2从点0移到无穷远处外力所作的功.olgdd题5-22图分析由库仑力的定义，根据Q1、Q：所受合力为零可求得Q.外力作功W应等于电场力作功W的负值，即W"=一W.求电场力作功的方法有两种：（1)根据功的定义，电场力作的功为W = J,,Edi其中E是点电荷QQ:产生的合电场强度(2）根据电场力作功与电势能差的关系，有

斯面，只有侧面的电场强度通量不为零，且  EdS = E  2πrL ，求出不同半径高斯面内的电 荷 q .即可解得各区域电场的分布. 解 作同轴圆柱面为高斯面，根据高斯定理  = 0 E 2πrL q/ε r ＜R1 ， q = 0 E1 = 0 在带电面附近，电场强度大小不连续，电场强度有一跃变 R1 ＜r ＜R2 ， q = λL ε r λ E 0 2 2π = r ＞R2， q = 0 E3 = 0 在带电面附近，电场强度大小不连续，电场强度有一跃变 2π 0 2π 0 0 Δ ε σ ε rL λL ε r λ E = = = 这与5 －20 题分析讨论的结果一致. 5 －22 如图所示，有三个点电荷Q1 、Q2 、Q3 沿一条直线等间距分布且Q1 ＝Q3 ＝Q. 已知其中任一点电荷所受合力均为零，求在固定Q1 、Q3 的情况下，将Q2从点O 移到无穷 远处外力所作的功. 分析 由库仑力的定义，根据Q1 、Q3 所受合力为零可求得Q2 .外力作功W′应等于电场力 作功W 的负值，即W′＝－W.求电场力作功的方法有两种：(1)根据功的定义，电场力作的功 为 Edl 0 2  W = Q 其中E 是点电荷Q1 、Q3 产生的合电场强度. (2) 根据电场力作功与电势能差的关系，有

W=0.(V。-V.)=0.其中V是Q、Q：在点产生的电势（取无穷远处为零电势）.解1由题意Q1所受的合力为零aQ+0/4ne.(2a)0. =-10 =-10解得由点电荷电场的叠加，Qi、Q；激发的电场在y轴上任意一点的电场强度为QyE = Ei, + Esy =2元0(d +y2)2将Q：从点0沿y轴移到无穷远处，（沿其他路径所作的功相同，请想一想为什么？）外力所作的功为eOW"=-I'QE.dl=--J-4[-1] 2m0(+y-=8元d解2与解1相同，在任一点电荷所受合力均为零时Q,=-Q，并由电势的叠加得Q1、Q:在点O的电势0.0Vo- 4a 4ma 2m0d将Q从点O推到无穷远处的过程中，外力作功02W"=-Q,V=8元00d比较上述两种方法，显然用功与电势能变化的关系来求解较为简洁.这是因为在许多实际问题中直接求电场分布困难较大，而求电势分布要简单得多5一27两个同心球面的半径分别为R和R2，各自带有电荷Q1和Q2.求：（1）各区域电势分布，并画出分布曲线：（2）两球面间的电势差为多少？题5-27图

( ) W = Q2 V0 −V = Q2V0 其中V0 是Q1 、Q3 在点O 产生的电势(取无穷远处为零电势). 解1 由题意Q1 所受的合力为零 ( ) 0 4π 4π 2 2 0 3 2 1 0 2 1 + = ε d Q Q ε d Q Q 解得 Q Q Q 4 1 4 1 2 = − 3 = − 由点电荷电场的叠加，Q1 、Q3 激发的电场在y 轴上任意一点的电场强度为 ( ) 3 / 2 2 2 0 1 3 2πε d y Q E E E y y y + = + = 将Q2 从点O 沿y 轴移到无穷远处，(沿其他路径所作的功相同，请想一想为什么？)外力所 作的功为 ( ) ε d Q y ε d y Q W Q Q y 0 2 3/ 2 2 2 0 0 0 2 8π d 4 2π 1 d = +         = −  = − −     E l 解2 与解1相同，在任一点电荷所受合力均为零时 Q Q 4 1 2 = − ，并由电势 的叠加得Q1 、Q3 在点O 的电势 ε d Q ε d Q ε d Q V 0 0 3 0 1 0 4π 4π 2π = + = 将Q2 从点O 推到无穷远处的过程中，外力作功 ε d Q W Q V 0 2 2 0 8π  = − = 比较上述两种方法，显然用功与电势能变化的关系来求解较为简洁.这是因为在许多实际问 题中直接求电场分布困难较大，而求电势分布要简单得多. 5 －27 两个同心球面的半径分别为R1 和R2 ，各自带有电荷Q1 和Q2 .求：(1) 各区域电 势分布，并画出分布曲线；(2) 两球面间的电势差为多少？

分析通常可采用两种方法(1）由于电荷均匀分布在球面上，电场分布也具有球对称性，因此，可根据电势与电场强度的积分关系求电势.取同心球面为高斯面，借助高斯定理可求得各区域的电场强度分布，再由V，=E·d/可求得电势分布。（2）利用电势叠加原理求电势.一个均匀带电的球面，在球面外产生的电势为0V=ATeS在球面内电场强度为零，电势处处相等，等于球面的电势0V=AneR其中R是球面的半径.根据上述分析，利用电势叠加原理，将两个球面在各区域产生的电势叠加，可求得电势的分布。解1（1）由高斯定理可求得电场分布(rR)4元6.1由电势V=E·dI可求得各区域的电势分布.当≤Ri时，有V=["E, di+["E, di+f'E, d!-11+9+0,=0+[1+4元eRR」+4元oRQtQ"4neoR* 4元eok当R≤r<R2时，有V,-I"E, dl+J'E, dl2[1.1]+9+04元[R]4neRQ29+14元eor+4元ek当r≥R2时，有V-'E,-dl-9+04元8

分析 通常可采用两种方法(1) 由于电荷均匀分布在球面上，电场分布也具有球对称性，因 此，可根据电势与电场强度的积分关系求电势.取同心球面为高斯面，借助高斯定理可求得 各区域的电场强度分布，再由   =  p Vp E dl 可求得电势分布.(2) 利用电势叠加原理求电势. 一个均匀带电的球面，在球面外产生的电势为 ε r Q V 4π 0 = 在球面内电场强度为零，电势处处相等，等于球面的电势 ε R Q V 4π 0 = 其中R 是球面的半径.根据上述分析，利用电势叠加原理，将两个球面在各区域产生的电势 叠加，可求得电势的分布. 解1 (1) 由高斯定理可求得电场分布 ( ) ( ) ( ) 2 2 0 1 2 3 2 1 2 0 1 2 1 1 4π 4π 0 r R ε r Q Q R r R ε r Q r R r r  + = =   =  E e E e E 由电势   =  r V E dl 可求得各区域的电势分布. 当r≤R1 时，有 0 2 2 0 1 1 0 2 1 2 0 1 2 1 1 1 2 3 4π 4π 4π 1 1 4π 0 d d d 2 2 1 1 ε R Q ε R Q ε R Q Q ε R R Q V R R R R r = + + +      = + − =  +  +      E l E l E l 当R1 ≤r≤R2 时，有 0 2 2 0 1 0 2 1 2 0 2 1 2 2 3 4π 4π 4π 1 1 4π d d 2 2 ε R Q ε r Q ε R Q Q ε r R Q V R R r = + + +      = − =  +     E l E l 当r≥R2 时，有 ε r Q Q V r 0 1 2 3 3 4π d + =  =   E l