《大学物理学》课程作业习题（含解答）第10章作业题

10-8波源作简谐运动，其运动方程为y=4.0×10~cos240元t（m)，它所形成的波形以30ms-1的速度沿一直线传播。（1）求波的周期及波长：（2）写出波动方程。分析已知波源运动方程求波动物理量及波动方程，可先将运动方程与其一般形式y=Acos(ot+)进行比较，求出振幅A、角频率α及初相p0，而这三个物理量与波动方程的一般形式 y=Acos[o(t-x/u)+p]中相应的三个物理量是相同的。再利用题中已知的波速u及公式の=2V=2元/T和入=uT即可求解解（1）由已知的运动方程可知，质点振动的角频率の=240元sl。根据分析中所述，波的周期就是振动的周期，故有T=2元/0=8.33x10 s波长为=ul =0.25 m（2）将已知的波源运动方程与简谐运动方程的一般形式比较后可得A=4.0×10-mQ=240元s-，po=0故以波源为原点，沿×轴正向传播的波的波动方程为y= Acos(o(t-x/u)+ ]=4.0×10- cos(240元/t-8元x) (m)10-10波源作简谐运动，周期为0.02s，若该振动以100m：s-的速度沿直线传播，设1=0时，波源处的质点经平衡位置向正方向运动，求：（1）距波源15.0m和5.0m两处质点的运动方程和初相；（2）距波源为16.0m和17.0m的两质点间的相位差。分析（1）根据题意先设法写出波动方程，然后代入确定点处的坐标，即得到质点的运动方程。并可求得振动的初相。（2）波的传播也可以看成是相位的传播。。由波长入的物理含意，可知波线上任两点间的相位差为Ag=2元Ax/入（1）由题给条件T=0.02s，u=100m·s，可得解 = 2元/T=100元m·s-l; ^=uT =2m当1=0时，波源质点经平衡位置向正方向运动，因而由旋转失量法可得该质点的初相为00=一元/2（或3元/2）：若以波源为坐标原点，则波动方程为y= Acos[100元(t-x/100)-元/2]距波源为xl=15.0m和x2=5.0m处质点的运动方程分别为J= Acos(100t-15.5元)y2 = Acos(100t - 5.5元)它们的初相分别为910=—15.5元和910=—5.5元（若波源初相取90=3元/2，则初相910=

10-8 波源作简谐运动，其运动方程为 4.0 10 cos240πt (m) −3 y =  ，它所形成的波形 以 30ｍ·ｓ-1 的速度沿一直线传播．（1） 求波的周期及波长；（2） 写出波动方程． 分析 已知波源运动方程求波动物理量及波动方程，可先将运动方程与其一般形式 y = Acos(t +) 进行比较，求出振幅 A、角频率 ω 及初相 φ0 ，而这三个物理量与波动方 程的一般形式  ( )  0 y = Acos  t − x / u + 中相应的三个物理量是相同的．再利用题中已知 的波速 u 及公式 ω＝2πν ＝2π／T 和 λ＝u T 即可求解． 解 （1） 由已知的运动方程可知，质点振动的角频率 1 240π s − ω = ．根据分析中所述， 波的周期就是振动的周期，故有 2π/ 8.33 10 s −3 T = ω =  波长为 λ＝uT ＝0.25 ｍ （２） 将已知的波源运动方程与简谐运动方程的一般形式比较后可得 A ＝4.0 ×10-3m， 1 240π s − ω = ，φ0 ＝0 故以波源为原点，沿 x 轴正向传播的波的波动方程为  ( )  4.0 10 cos(240π 8π ) (m) cos / 3 0 t x y A ω t x u =  − = − + − 10-10 波源作简谐运动，周期为 0.02ｓ，若该振动以 100m·ｓ-1 的速度沿直线传播， 设 t ＝0 时，波源处的质点经平衡位置向正方向运动，求：（1） 距波源 15.0ｍ 和 5.0 m 两 处质点的运动方程和初相；（2） 距波源为 16.0 m 和 17.0m 的两质点间的相位差． 分析 （1） 根据题意先设法写出波动方程，然后代入确定点处的坐标，即得到质点的 运动方程．并可求得振动的初相．（2） 波的传播也可以看成是相位的传播．由波长 λ 的物 理含意，可知波线上任两点间的相位差为 Δφ＝2πΔx／λ． 解 （1） 由题给条件 1 0 02 s 100 m s − T = . , u =  ，可得 2π/ 100π m s ; 2 m 1 = =  = = − ω T λ uT 当 t ＝0 时，波源质点经平衡位置向正方向运动，因而由旋转矢量法可得该质点的初相 为 φ0 ＝－π／2（或 3π／2）．若以波源为坐标原点，则波动方程为 y = Acos100π(t − x/100)− π/2 距波源为 x1 ＝15.0 m 和 x2 ＝5.0 m 处质点的运动方程分别为 ( ) cos(100πt 5.5π) cos 100πt 15.5π 2 1 = − = − y A y A 它们的初相分别为 φ10 ＝－15.5π 和 φ10 ＝－5.5π（若波源初相取 φ0＝3π/2，则初相 φ10 ＝

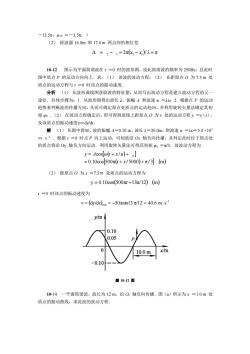
—13.5元， 010 =—3.5元。）（2）距波源16.0m和17.0m两点间的相位差△ = 2- 1=2元(x2-x)/α=元10-12图示为平面简谐波在1=0时的波形图，设此简谐波的频率为250Hz，且此时图中质点P的运动方向向上。求：（1）该波的波动方程：（2）在距原点0为7.5m处质点的运动方程与1=0时该点的振动速度分析（1）从波形曲线图获取波的特征量，从而写出波动方程是建立波动方程的又一途径。具体步骤为：1、从波形图得出波长入、振幅A和波速u=1D；2.根据点P的运动趋势来判断波的传播方向，从而可确定原点处质点的运动趋向，并利用旋转矢量法确定其初（2）在波动方程确定后，即可得到波线上距原点0为×处的运动方程y=y（1），相0：及该质点的振动速度u=dy/dr.解（1）从图中得知，波的振幅A=0.10m，波长入=20.0m，则波速u=1v=5.0×103m·s。根据1=0时点P向上运动，可知波沿Ox轴负向传播，并判定此时位于原点处的质点将沿Oy轴负方向运动。利用旋转矢量法可得其初相go元/3．故波动方程为y= Acos[o(t+x/u)+ 0] =0.10cos[500元(+x/5000)+元/3] (m)（2）距原点0为x=7.5m处质点的运动方程为y=0.10cos(500元t+13/12) (m)1 =0 时该点的振动速度为v= (dy/dt)=0 = -50元sin13 元/12= 40.6 m sy/m 0.100x/m10.0m0.10题10-12图10-14一平面简谐波，波长为12m，沿Q轴负向传播。图（a）所示为x=1.0m处质点的振动曲线，求此波的波动方程

－13.5π，φ10 ＝－3.5π．） （2） 距波源 16.0m 和 17.0 m 两点间的相位差 Δ = 2 − 1 = 2π(x2 − x1 )/ λ = π 10-12 图示为平面简谐波在 t ＝0 时的波形图，设此简谐波的频率为 250Hz，且此时 图中质点 P 的运动方向向上．求：（1） 该波的波动方程；（2） 在距原点 O 为 7.5 m 处 质点的运动方程与 t ＝0 时该点的振动速度． 分析 （1） 从波形曲线图获取波的特征量，从而写出波动方程是建立波动方程的又一 途径．具体步骤为：1. 从波形图得出波长 λ、振幅 A 和波速 u ＝λ；2. 根据点 P 的运动 趋势来判断波的传播方向，从而可确定原点处质点的运动趋向，并利用旋转矢量法确定其初 相 φ0 ．（2） 在波动方程确定后，即可得到波线上距原点 O 为 x 处的运动方程 y ＝y（t）， 及该质点的振动速度＝dy/dt． 解 （1） 从图中得知，波的振幅 A＝0.10 m，波长 λ＝20.0m，则波速 u ＝λ＝5.0 ×103 ｍ·ｓ-1 ．根据 t ＝0 时点 P 向上运动，可知波沿 Ox 轴负向传播，并判定此时位于原点处 的质点将沿 Oy 轴负方向运动．利用旋转矢量法可得其初相 φ0 ＝π/3．故波动方程为  ( )  0.10cos500π( /5000) π /3 (m) cos / 0 = + + = + + t x y A ω t x u （2） 距原点 O 为 x ＝7.5ｍ 处质点的运动方程为 y = 0.10cos(500πt +13π/12) (m) t ＝0 时该点的振动速度为 ( ) -1 0 = d /d = −50πsin13 π/12 = 40.6 ms t= v y t 题 10-12 图 10-14 一平面简谐波，波长为 12 m，沿 Ox 轴负向传播．图（a）所示为 x ＝1.0 m 处 质点的振动曲线，求此波的波动方程．

y/m ↓0.4070.20QVy/mTo(a)(b)题10-14 图分析该题可利用振动曲线来获取波动的特征量，从而建立波动方程。求解的关键是如何根据图（a）写出它所对应的运动方程。较简便的方法是旋转矢量法解由图（a）可知质点振动的振幅A=0.40m，1=0时位于×=1.0m处的质点在A/2处并向Oy轴正向移动.据此作出相应的旋转失量图（b），从图中可知。=一元/3：又由图（a）可知，1=5s时，质点第一次回到平衡位置，由图（b）可看出ot=5元/6，因而得角频率の=（元/6）sl由上述特征量可写出x=1.0m处质点的运动方程为y=0.04cos[-] (m)将波速u=入/T=0//2元=1.0m·s及x=1.0m代入波动方程的一般形式y=Acos[o(t+x/u)+]中，并与上述×=1.0m处的运动方程作比较，可得9o=一元/2，则波动方程为(++x/10)-号(m)y=0.04cos10-16平面简谐波的波动方程为y=0.08cos(4元t-2z）(m).求：（1）1=2.1s时波源及距波源0.10m两处的相位：（2）离波源0.80m及0.30m两处的相位差.解（1）将1=2.1s和x=0代入题给波动方程，可得波源处的相位1 =8.4元将1=2.1s和x=0.10m代入题给波动方程，得0.10m处的相位为2=8.2元

题 10-14 图 分析 该题可利用振动曲线来获取波动的特征量，从而建立波动方程．求解的关键是如 何根据图（a） 写出它所对应的运动方程．较简便的方法是旋转矢量法． 解 由图（a）可知质点振动的振幅 A ＝0.40 ｍ，t ＝0 时位于 x ＝1.0 m 处的质点在 A/2 处并向 Oy 轴正向移动．据此作出相应的旋转矢量图（b），从图中可知  0 = −π /3 ．又 由图（a）可知，t ＝5 s 时，质点第一次回到平衡位置，由图（b）可看出 ωt ＝5π／6，因 而得角频率 ω＝（π/6） s -1 ．由上述特征量可写出 x ＝1.0 m 处质点的运动方程为 (m) 3 π 6 π y 0.04cos       = t − 将 波 速 1 / / 2π 1.0 m s − u = λ T = ωλ =  及 x ＝ 1.0 m 代 入 波 动 方 程的 一 般 形 式  ( )  0 y = Acos  t + x / u + 中，并与上述 x ＝1.0 m 处的运动方程作比较，可得 φ0 ＝－π ／2，则波动方程为 ( ) (m) 2 π /10 6 π y 0.04cos       = t + x − 10-16 平面简谐波的波动方程为 y = 0.08cos(4πt − 2πx) (m)． 求：（1） t ＝2.1 s 时波源及距波源 0.10m 两处的相位；（2） 离波源 0.80 m 及 0.30 m 两处的相位差． 解 （1） 将 t ＝2.1 s 和 x ＝0 代入题给波动方程，可得波源处的相位 1 = 8.4π 将 t ＝2.1 s 和 x′＝0.10 m 代入题给波动方程，得 0.10 m 处的相位为 2 = 8.2π

（2）从波动方程可知波长1=1-0.80m与x2=0.30m两点间的相m.：位差△ =2元元-△x//=元10-18有一波在介质中传播，其波速u=1.0×10msl，振幅A=1.0×10-4m，频率1.0×10°Hz.若介质的密度为p=8.0×10kg:m2，求：（1）该波的能流密度：（2）1min内垂直通过4.0×10m2的总能量，解（1）由能流密度丨的表达式得1=puAo2=2元"puAPy2=1.58×10”W.m*2（2）在时间间隔At=60s内垂直通过面积S的能量为W = P.Nt= IS .Nt=3.79×10' J10-20如图所示，两相干波源分别在P、两点处，它们发出频率为、波长为，初相相同的两列相干波。设PQ=3/2，R为PQ连线上的一点。求：（1）自P、Q发出的两列波在R处的相位差：（2）两波在R处干涉时的合振幅CR题10-20图分析因两波源的初相相同，两列波在点R处的相位差A仍与上题一样，由它们的波程差决定，因R处质点同时受两列相于波的作用，其振动为这两个同频率、同振动方向的简谐运动的合成，合振幅A=/4+A+24.4.cosAp解（1）两列波在R处的相位差为=2元/=3元（2）由于△=3元，则合振幅为A=A +A +2AAcos3元=4-A]10-21两相干波波源位于同一介质中的A、B两点，如图（a）所示.其振幅相等、频率皆为100Hz，B比A的相位超前元.若A、B相距30.0m，波速为u=400m-s-l，试求AB连线上因干涉而静止的各点的位置

（2） 从波动方程可知波长 λ＝1.0 m．这样，x1 ＝0.80 m 与 x2 ＝0.30 m 两点间的相 位差 Δ = 2ππΔx/ λ = π 10-18 有一波在介质中传播，其波速 u ＝1.0 ×103m·s-1 ，振幅 A ＝1.0 ×10-4 m，频率 ν ＝ 1.0 ×103Hz．若介质的密度为 ρ ＝8.0×102 kg·m-3 ，求：（1） 该波的能流密度；（2） 1 min 内垂直通过 4.0 ×10-4m2 的总能量． 解 （1） 由能流密度 I 的表达式得 2 2 2 2 2 5 2 2 1 58 10 W m 2 1 − I = uA  =  uA v = .   （2） 在时间间隔 Δt ＝60 s 内垂直通过面积 S 的能量为 3 79 10 J 3 W = P t = IS t = .  10-20 如图所示，两相干波源分别在 P、Q 两点处，它们发出频率为 ν、波长为 λ，初 相相同的两列相干波．设 PQ ＝3λ/2，R 为 PQ 连线上的一点．求：（1） 自 P、Q 发出 的两列波在 R 处的相位差；（2） 两波在 R 处干涉时的合振幅． 题 10-20 图 分析 因两波源的初相相同，两列波在点 R 处的相位差 Δφ 仍与上题一样，由它们的波程 差决定．因 R 处质点同时受两列相干波的作用，其振动为这两个同频率、同振动方向的简 谐运动的合成，合振幅 = + + 2 1 2 cos 2 2 2 A A1 A A A ． 解 （1） 两列波在 R 处的相位差为 Δ = 2πΔr/ λ = 3π （2） 由于 Δ = 3π ，则合振幅为 1 2 1 2 2 2 2 1 A = A + A + 2A A cos3 = A − A 10-21 两相干波波源位于同一介质中的 A、B 两点，如图（a）所示．其振幅相等、频 率皆为 100 Hz，B 比 A 的相位超前 π．若 A、B 相距 30.0m，波速为 u ＝400 m·s-1 ，试求 AB 连线上因干涉而静止的各点的位置．

30mx(b)(a)题10-21 图2元个，因此，两列振幅相同的相干分析两列相干波相遇时的相位差△=2-波因干涉而静止的点的位置，可根据相消条件△=(2k+1)元获得解以A、B两点的中点0为原点，取坐标如图（b）所示.两波的波长均为\=u/v=4.0m。在A、B连线上可分三个部分进行讨论。1．位于点A左侧部分△ = μ- A-2元(g-r)=-14元因该范围内两列波相位差恒为2元的整数倍，故干涉后质点振动处处加强，没有静止的点，2．位于点B右侧部分 = B= A-2元(-r)=16元显然该范围内质点振动也都是加强，无干涉静止的点3．在A、B两点的连线间，设任意一点P距原点为x.因rg=15-x，TA=15+x，则两列波在点P 的相位差为A = B- A-2元(g-r)/α=(x+1)根据分析中所述，干涉静止的点应满足方程x(x+ 1)元 =(52k +1)/元得x=2km (k=0,±1,±2,.)因x≤15m，故k<7.即在A、B之间的连线上共有15个静止点，10-24一弦上的驻波方程式为y=3.0x10-2cos(1.6x)cos(550元t) (m)（1）若将此驻波看成是由传播方向相反，振幅及波速均相同的两列相干波叠加而成的，求它们的振幅及波速：（2）求相邻波节之间的距离：（3）求1=3.0×10-3s时位于x=0.625m处质点的振动速度分析（1）采用比较法。将本题所给的驻波方程，与驻波方程的一般形式相比较即可求得振幅、波速等。（2）由波节位置的表达式可得相邻波节的距离。（3）质点的振动速度可按速度定义=dy/dl求得

题 10-21 图 分析 两列相干波相遇时的相位差 λ 2πΔr Δ = 2 − 1 − ．因此，两列振幅相同的相干 波因干涉而静止的点的位置，可根据相消条件 Δ = (2k +1)π 获得． 解 以 A、B 两点的中点 O 为原点，取坐标如图（b）所示．两波的波长均为 λ＝u/＝ 4.0 m．在 A、B 连线上可分三个部分进行讨论． 1. 位于点 A 左侧部分 Δ = B − A − 2π(rB − rA ) = −14π 因该范围内两列波相位差恒为 2π 的整数倍，故干涉后质点振动处处加强，没有静止的点． 2. 位于点 B 右侧部分 Δ = B − A − 2π(rB − rA ) =16π 显然该范围内质点振动也都是加强，无干涉静止的点． 3. 在 A、B 两点的连线间，设任意一点 P 距原点为 x．因 r =15 − x B ，r =15+ x A ， 则两列波在点 P 的相位差为 Δ = B − A − 2π(rB − rA )/ λ = (x +1)π 根据分析中所述，干涉静止的点应满足方程 x(x +1)π = (52k +1)π 得 x = 2k m (k = 0,1,2,.) 因 x≤15 m，故 k≤7．即在 A、B 之间的连线上共有 15 个静止点． 10-24 一弦上的驻波方程式为 3.0 10 cos(1.6π )cos(550π ) (m) 2 y x t − =  （1） 若将此驻波看成是由传播方向相反，振幅及波速均相同的两列相干波叠加而成的，求 它们的振幅及波速；（2） 求相邻波节之间的距离；（3） 求 t ＝3.0 ×10-3 s 时位于 x＝0.625 m 处质点的振动速度． 分析 （1） 采用比较法．将本题所给的驻波方程，与驻波方程的一般形式相比较即可 求得振幅、波速等．（2） 由波节位置的表达式可得相邻波节的距离．（3） 质点的振动速 度可按速度定义 v ＝dy/dt 求得．

解（1）将已知驻波方程=3.0×10-~cos(1.6元x)cos(550元t) (m)与驻波方程的一般形式y=2Acos(2元x/a)cos(2元ot）作比较，可得两列波的振幅A=1.5×10-m，波长入=1.25m=275Hz，则波速u=入v=343.8msl（2）相邻波节间的距离为Ar=+-x =[2(k+1)+1/4-(2k+1)a/4=/2=0.625m（3）在1=3.0×103s时，位于x=0.625m处质点的振动速度为v= dy/dt =-16.5元cos(1.6元x)cos(550元t)=-46.2 m s-面积为1.0m2的窗户开向街道，街中噪声在窗口的声强级为80dB.问有多少10-27“声功率”传入窗内？分析首先要理解声强、声强级、声功率的物理意义，并了解它们之间的相互关系。声强是声波的能流密度I，而声强级L是描述介质中不同声波强弱的物理量。它们之间的关系为L=lg（Ilo），其中lo=1.0×10-12W-m2为规定声强。L的单位是贝尔（B），但常用的单位是分贝（dB），且1B=10dB.声功率是单位时间内声波通过某面积传递的能量，由于窗户上各处的1相同，故有P=IS.解根据分析，由L=lg（1/1o）可得声强为1 =10L lo则传入窗户的声功率为P =IS =10LloS =1.0×104 W10-28若在同一介质中传播的，频率分别为1200Hz和400Hz的两声波有相同的振幅。求：（1）它们的强度之比；（2）两声波的声强级差。解（1）因声强I=puA/2，则两声波声强之比1,/1,=0f /og =9（2）因声强级L=lg（I/Io），则两声波声强级差为AL = lg(, / 10)-Ig(1, / 10)= Ig(1, / 12)= 0.954 B= 9.54 dB10-29一警车以25m·s的速度在静止的空气中行驶，假设车上警笛的频率为800Hz.求：（1）静止站在路边的人听到警车驶近和离去时的警笛声波频率：（2）如果警

解 （1） 将已知驻波方程 3.0 10 cos(1.6π )cos(550π ) (m) 2 y x t − =  与驻波方程的一般形式 y = 2Acos(2πx/ λ)cos(2πvt) 作比较，可得两列波的振幅 A ＝1.5 ×10-2 m，波长 λ＝1.25 m，频率＝275 Hz，则波速 u ＝λ＝343.8m·s-1 ． （2） 相邻波节间的距离为  ( )  ( ) 2 0 625 m k 1 k 2 1 1 4 2 1 4 / . / / = =  = + − = + + − +  x x x k  k  （3） 在 t ＝3.0 ×10-3 s 时，位于 x＝0.625 m 处质点的振动速度为 ( ) ( ) 1 46.2 m s d / d 16.5πcos 1.6π cos 550π − = −  v = y t = − x t 10-27 面积为 1.0 m2 的窗户开向街道，街中噪声在窗口的声强级为 80dB．问有多少 “声功率”传入窗内？ 分析 首先要理解声强、声强级、声功率的物理意义，并了解它们之间的相互关系．声 强是声波的能流密度 I，而声强级 L 是描述介质中不同声波强弱的物理量．它们之间的关系 为 L ＝lg（I /I0 ），其中 I0 ＝1.0 ×10-12 W·m-2 为规定声强．L 的单位是贝尔（B），但常 用的单位是分贝（dB），且 1 B ＝10 dB．声功率是单位时间内声波通过某面积传递的能量， 由于窗户上各处的 I 相同，故有 P ＝IS． 解 根据分析，由 L ＝lg（I ／I0 ）可得声强为 I ＝10L I0 则传入窗户的声功率为 P ＝IS ＝10L I0 S ＝1.0 ×10-4 W 10-28 若在同一介质中传播的，频率分别为 1200 Hz 和 400 Hz 的两声波有相同的振 幅．求：（1） 它们的强度之比；（2） 两声波的声强级差． 解 （1） 因声强 2 2 2 I = uA  / ，则两声波声强之比 9 2 2 2 I 1 / I 2 =1 /  = （2） 因声强级 L ＝lg（I ／I0 ），则两声波声强级差为 ( ) ( ) ( ) 0 954 B 9 54 dB lg 1 0 lg 2 0 lg 1 2 . . / / / = = L = I I − I I = I I 10-29 一警车以 25 m·s-1 的速度在静止的空气中行驶，假设车上警笛的频率为 800 Hz．求：（1） 静止站在路边的人听到警车驶近和离去时的警笛声波频率；（2） 如果警

车追赶一辆速度为15m?sl的客车，则客车上人听到的警笛声波的频率是多少？（设空气中的声速u=330m=s!分析由于声源与观察者之间的相对运动而产生声多普勒效应,由多普勒频率公式可解得结果。在处理这类问题时，不仅要分清观察者相对介质（空气）是静止还是运动，同时也要分清声源的运动状态。（1）根据多普勒频率公式，当声源（警车）以速度0.=25ms’运动时，静止于路边的观察者所接收到的频率为0'=0-uty警车驶近观察者时，式中前取“一"号，故有= = 86 警车驶离观察者时，式中：前取“+"号，故有= 743.7 Hz0.=0u+V（2）声源（警车）与客车上的观察者作同向运动时，观察者收到的频率为= 743.7 Hzoh="u+v

车追赶一辆速度为 15m·s-1 的客车，则客车上人听到的警笛声波的频率是多少？ （设空气 中的声速 u ＝330m·s-1 ） 分析 由于声源与观察者之间的相对运动而产生声多普勒效应，由多普勒频率公式可解 得结果．在处理这类问题时，不仅要分清观察者相对介质（空气）是静止还是运动，同时也 要分清声源的运动状态． 解 （1） 根据多普勒频率公式，当声源（警车）以速度 vs ＝25 m·s-1 运动时，静止 于路边的观察者所接收到的频率为 s u v u  v = v 警车驶近观察者时，式中 vs 前取“－”号，故有 865.6 Hz 1 = −  = s u v u v v 警车驶离观察者时，式中 vs 前取“＋”号，故有 743.7 Hz 2 = +  = s u v u v v （2） 声源（警车）与客车上的观察者作同向运动时，观察者收到的频率为 743.7 Hz 2 = +  = s u v u v v