《大学物理学》课程作业习题（含解答）No.10 安培定律、磁力、磁介质

安培定律磁力磁介质《大学物理AI》作业No.10一、选择题：（注意：题目中可能有一个或几个正确答案）1．如图，两根直导线ab和cd沿半径方向被接到一个截面处处相等的铁环上，稳恒电流I从α端流入而从d端流出，则磁感应强度B沿图中闭合路径L的积分f,B.dI等于［D]4(A) μol(C) ol001解：电流I从b点分流，I=I+1。设铁环总电阻为R，由电阻公式有dR=P,R=2RR=R又因U=U即，得-号fB-ad7-, ol所以：故选D2．无限长载流空心圆柱导体的内外半径分别为a、b，电流在导体截面上均匀分布，则空间各处B的大小与场点到圆柱中心轴线距离r的关系定性地如图所示。正确的图是：【B解：由安培环路定理有：r<a时，B=0$B.dia<r<b时，r-ah-2-03=2元(b2-α2)B）由此知：随着r的增加，Br曲线的斜率将减小dr"2(b3-a') (1+)

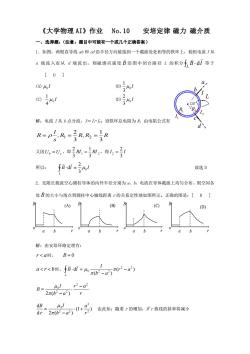
《大学物理 AI》作业 No.10 安培定律 磁力 磁介质 一、选择题：（注意：题目中可能有一个或几个正确答案） 1．如图，两根直导线 ab 和 cd 沿半径方向被接到一个截面处处相等的铁环上，稳恒电流 I 从 a 端流入而从 d 端流出，则磁感应强度 B  沿图中闭合路径 L 的积分   L B l   d 等于 [ D ] (A) I 0 (B) I 0 3 1  (C) I 0 4 1  (D) I 0 3 2  解：电流 I 从 b 点分流，I＝I1+I2。设铁环总电阻为 R，由电阻公式有 R R R R s l R 3 1 , 3 2 , =  1 = 2 = 又因 Ub = Uc ，即 1 2 3 1 3 2 RI = RI ，得 I I 3 2 2 = 所以： B l I L 0 3 2  d =     故选 D 2．无限长载流空心圆柱导体的内外半径分别为 a、b，电流在导体截面上均匀分布，则空间各 处 B  的大小与场点到圆柱中心轴线距离 r 的关系定性地如图所示。正确的图是：[ B ] 解：由安培环路定理有： r  a 时， B = 0 a  r  b 时， ( ) ( ) d 2 2 0 2 2 r a b a I B l L − −  =       r r a b a I B 2 2 2 2 0 2 ( ) −  − =   (1 ) d 2 ( ) d 2 2 2 2 0 r a b a I r B  + − =   由此知：随着 r 的增加，B~r 曲线的斜率将减小 B r o a b (B) B r o a b (A) a b B r o (C) B r o a b (D) a b c d I L  120 1 I 2 I R1 R2

B=L1r>b时，T故选B3.如图，一无限长直载流导线与正三角形载流线圈在同一平面内，若长直导线固定不动，则载流三角形线圈将：「A(A）向着长直导线平移(B）离开长直导线平移(c)转动(D)不动解：建立如图所示的坐标轴，无限长的直电流在x>0处产生的磁感应强度为：B= 4ol方向2元1由安培定律公式，可得三角形线圈的三个边受力大小分别为Fa = 4ol B= 4olla 2元a2元aFxe = Fec IBl, d eworMgl/. dx+2元×c0s30°～3元2a式中1为三角形边长，各力方向如图所示，可见三角形不可能移动，合力为：ZF, = Fxe sin 60° -FBc in 60°=0F--Fa2Fieco60-4-2Fm1+2元0令=(>0)，有S---x-)=- 40l/2(1-2)<0da2元+2元1+又F，1-0=0，所以载流线圈所受合力始终向着长直电流，故载流线圈只能向着长直电流平动。故选A4.真空中电流元1d7与电流元12d7,之间的相互作用是这样进行的：【D(A）1id7,与I2d7,直接进行作用，且服从牛顿第三定律。(B）由I,d7,产生的磁场与IdT,产生的磁场之间相互作用，且服从牛顿第三定律

r  b 时， r r I B 1 2 0 =    故选 B 3．如图，一无限长直载流导线与正三角形载流线圈在同一平面内，若 长直导线固定不动，则载流三角形线圈将：[ A ] (A) 向着长直导线平移 (B) 离开长直导线平移 (C) 转动 (D) 不动 解：建立如图所示的坐标轴，无限长的直电流在 x>0 处产生的 磁感应强度为： x I B   2 0 １ = 方向  由安培定律公式，可得三角形线圈的三个边受力大小分别为： l a I I AB a I I FAB     2 2 0 1 2 0 1 2 = = ) 2 3 ln(1 cos30 3 d 2 d 0 1 2 cos3 0 0 1 2 2 a x I I l x I I F F BI l a l a C A A C B C = +  = = =    +      式中 l 为三角形边长，各力方向如图所示，可见三角形不可能移动，合力为： )] 2 3 ln(1 3 2 3 [ 2 2 cos60 sin 60 sin 60 0 0 1 2 a l a I I l F F F F F F x AB AC y AC BC = − +  = − − +  =  −  =     令 = (  0) a l ，有 ) 0 2 3 1 1 (1 2 ] 2 3 1 2 3 3 2 3 [1 d 2 d( ) 0 1 2 0 1 2  + = − − + = − −          Fx I I I I 又 Fx | =0 = 0 ，所以载流线圈所受合力始终向着长直电流，故载流线圈只能向着长直电流 平动。 故选 A 4．真空中电流元 1d 1 I l  与电流元 2d 2 I l  之间的相互作用是这样进行的：[ D ] (A) 1d 1 I l  与 2d 2 I l  直接进行作用，且服从牛顿第三定律。 (B) 由 1d 1 I l  产生的磁场与 2d 2 I l  产生的磁场之间相互作用，且服从牛顿第三定律。 1 I 2 I O y x 1 I 2 a I l A B C FAB  FAC  FBC 

(C）由Iid7,产生的磁场与12d,产生的磁场之间相互作用，但不服从牛顿第三定律。(D）由1d7,产生的磁场与I2d7,进行作用，或由12dz,产生的磁场与1id7,进行作用，且不服从牛顿第三定律。解：两个电流之间的相互作用是通过磁场进行的，不服从牛顿第三定律。由安培定律，一个电流元所受的力决定于另一个电流元在该电流元处产生的磁场及电流元本身，即dF,=I,d,×B,或dF,,=1,dl,×B,。故选D5．如图所示，一固定的载流大平板，在其附近，有一载流小线框能自由转动或平动。线框平面与大平板垂直，大平板的电流与线框中电流方向如图所示，则通电线框的运动情况从大平板向外看是：［C］(A)靠近大平板 AB(B)顺时针转动P(C)逆时针转动(D)离开大平板向外运动。解：因载流大平板产生的磁场平行于平板，方向如图所示。则线圈AL在磁场中所受的磁力矩为：M=P.×B故知：磁力矩方向垂直并指向载流大平板，所以从平板向外看，线圈逆时针转动。故选C6．关于稳恒磁场的磁场强度H的下列几种说法哪个是正确的？【](A）H仅与传导电流有关。（B）若闭合曲线内没有包围传导电流，则曲线上各点的H必为零。（C）若闭合曲线上各点的H均为零，则该曲线所包围传导电流的代数和为零。(D）以闭合曲线L为边缘的任意曲面的H通量均相等。解：磁场强度H不仅与传导电流有关，还与磁化电流有关，根据安培环路定理，fH.di-o若L上各点=0，则.d=0，。=0.根据磁场的性质，以闭合曲线L边缘的任意取面的B的通量相等，H通量不一定相等。二、填空题：1.两根长直导线通有电流I，在图示三种环路中，B·di分别等于：

(C) 由 1d 1 I l  产生的磁场与 2d 2 I l  产生的磁场之间相互作用，但不服从牛顿第三定律。 (D) 由 1d 1 I l  产生的磁场与 2d 2 I l  进行作用，或由 2d 2 I l  产生的磁场与 1d 1 I l  进行作用，且不服 从牛顿第三定律。 解：两个电流之间的相互作用是通过磁场进行的，不服从牛顿第三定律。 由安培定律，一个电流元所受的力决定于另一个电流元在该电流元处产生的磁场及电流元本 身，即 d 12 1d 1 B2 F I l    =  或 d 21 2d 2 B1 F I l    =  。 故选 D 5．如图所示，一固定的载流大平板，在其附近，有一载流小线框能自由转动或平动。线框平 面与大平板垂直，大平板的电流与线框中电流方向如图所示，则通电线框的运动情况从大平 板向外看是：[ C ] (A)靠近大平板 AB (B)顺时针转动 (C)逆时针转动 (D)离开大平板向外运动。 解：因载流大平板产生的磁场平行于平板，方向如图所示。则线圈 在磁场 中所受的磁力矩为： 故知：磁力矩方向垂直并指向载流大平板，所以从平板向外看，线圈逆时针转动。故选 C 6．关于稳恒磁场的磁场强度 H  的下列几种说法哪个是正确的？[ C ] (A) H  仅与传导电流有关。 (B) 若闭合曲线内没有包围传导电流，则曲线上各点的 H  必为零。 (C) 若闭合曲线上各点的 H  均为零，则该曲线所包围传导电流的代数和为零。 (D) 以闭合曲线Ｌ为边缘的任意曲面的 H  通量均相等。 解：磁场强度 H  不仅与传导电流有关，还与磁化电流有关，根据安培环路定理，   =  内 d 0 H l I L   若 L 上各点 H = 0  ，则  d = 0,  = 0. 0 H l I L   根据磁场的性质，以闭合曲线 L 边缘的任意取面的 B  的通量相等， H  通量不一定相等。 二、填空题： 1．两根长直导线通有电流 I，在图示三种环路中， B l    d  分别等于： M Pm B    =  B  Pm  2 I 1 I A B

Mol（对于环路a）(对于环路 b)。2μgl（对于环路c解：根据安培环路定理，f.B.d=o对于 a:f,B-d = Mol对于 b: f,B-dI=Po(I-I)=0对于 c: f,B-di=Ho(I+I)=2μol2．如图所示的空间区域内，分布着方向垂直于纸面的匀强磁场，在纸面内有一正方形边框abcd（磁场以边框为界），而三个角顶处开有很小的缺口，今有一束具有不同速度的电子由α缺口沿ad方向射入磁场区域，若b、℃两缺口处分别有电子射出，自此两处电子的速率之比vb/v解：因电子在匀强磁场中作圆周运动的半径为R-av而从b处射出的电子半径为：R，=ab，从c处射出的电子半径R。=ab，R-!Vb=所以，自此两处电子的速率之比R23.如图，一个均匀磁场B只存在于垂直图面的P平面右侧，B的方向垂直于图面向里。一质量为m，电荷为α的粒子以速度射入磁场，立在图面内与界面P成某一角度。那么粒子在从磁场中射出前是做半径为的圆周运动。如果q>0时，粒子在磁场中的路径与边界围成的平面区域的面积为S，那么g<0时，其路(-s径与边界围成的平面区域的面积为

I 0 （对于环路 a）。 ０ （对于环路 b）。 I 20 （对于环路 c）。 解：根据安培环路定理，   =  内 B l I L d 0   对于 a： B l I L d = 0     对于 b： d = 0 ( − ) = 0  B l I I L    对于 c： B l I I I L 0 2 0 d =  ( + ) =     2．如图所示的空间区域内，分布着方向垂直于纸面的匀强磁场， 在纸面内有一正方形边框 abcd（磁场以边框为界），而 a、b、c 三个角顶处开有很小的缺口，今有一束具有不同速度的电子由 a 缺口沿 ad 方向射入磁场区域，若 b、c 两缺口处分别有电子射出， 自此两处电子的速率之比 vb vc = 2 1 。 解： 因电子在匀强磁场中作圆周运动的半径为 v eB mv R =  而从 b 处射出的电子半径为： Rb ab 2 1 = ，从 c 处射出的电子半径 Rc = ab， 所以 ，自此两处电子的速率之比 2 1 = = c b c b R R v v 3．如图，一个均匀磁场 B  只存在于垂直图面的 P 平面右侧， B  的方向垂直于图面向里。一质量为ｍ，电荷为 q 的粒子以 速度 v  射入磁场， v  在图面内与界面 P 成某一角度。那么粒 子在从磁场中射出前是做半径为 | | qB mv 的圆周运动。 如果 q＞０时，粒子在磁场中的路径与边界围成的平面区域的面积为Ｓ，那么 q＜０时，其路 径与边界围成的平面区域的面积为 S qB mv − 2  ( ) 。 a b c d                                           B  P v  A • b I c c I a

n解：由带电粒子在磁场中的运动规律知：粒子在磁场中运动的半径为R=I，从入射点A,qBg>0和g1，其B~H关系为斜率大于1的直线b。抗磁质μ,<1，其B~H关系为斜率小于1的直线 c6.长直电缆由一个圆柱导体和一共轴圆筒状导体组成，两导体中有等值反向均匀电流I通过，其间充满磁导率为μ的均匀磁介质。则介质中离中心轴距离为的某点处的磁场强度大小1ul2元2元H=，磁感应强度的大小B=解：以轴线为圆心，「为半径作一圆形回路

H B a b c o 解：由带电粒子在磁场中的运动规律知：粒子在磁场中运动的半径为 | | qB mv R = ，从入射点 A， q>0 和 q<0 的粒子运动的轨迹不同，二轨迹在 A 点相切， v  为公共切线。由对称性可知： S qB mv S = − 2  ( ) 4．如图所示，在真空中有一半径为 a 的 3／4 圆弧形的导线，其中 通以稳恒电流 I，导线置于均匀外磁场 B  中，且 B  与导线所在平面 垂直，则该载流导线  bc 所受的磁力大小为 2aBI 。 解：在均匀磁场中，载流圆弧  bc 所受的磁力与通以同 样电流的弦线 bc 所受的磁力大小相等，其大小由安培 定律可得： F = BI 2a = 2aBI 5．图示为三种不同的磁介质的 B～H 关系曲线，其中虚 线表示的是 B = 0H 的关系。试说明 a、b、c 各代表哪 一类磁介质的 B～H 关系曲线： a 代表 铁磁质 的 B～H 关系曲线。 b 代表 顺磁质 的 B～H 关系曲线。 c 代表 抗磁质 的 B～H 关系曲线。 解：因  = 0r ,B = H ，对于铁磁质，  r 不是常数，其 B～H 关系为曲线 a。 顺磁质 r 1 ，其 B～H 关系为斜率大于 1 的直线 b。 抗磁质 r 1 ，其 B～H 关系为斜率小于 1 的直线 c。 6．长直电缆由一个圆柱导体和一共轴圆筒状导体组成，两导体中有等值反向均匀电流 I 通过， 其间充满磁导率为  的均匀磁介质。则介质中离中心轴距离为 r 的某点处的磁场强度大小 H = r I 2 ，磁感应强度的大小 B = r I   2 。 解：以轴线为圆心，r 为半径作一圆形回路， a b B  I c a o P P v  A • S S

由有磁介质时安培环路定律fH.d7=ZI。可得：fH.d/ -H.2r=1于是r处磁场强度大小为：H=2元1ulB=μH，故r处磁感应强度大小为：B=μH=2元三、计算题：1.如图所示，一半径为R的均匀带电无限长直圆筒电荷面密度为，该筒以角速度の绕其轴线匀速旋转，试求圆筒内部的磁感应强度。解：带电圆筒旋转相当于圆筒表面有面电流，单位长度上电流为；i=2元R8.-=RS021与长直通电螺线管内磁场分布类似。圆筒内为均匀磁场，B的方向与の一致（若<0，则相反)。圆筒外B=0。作如图所示的安培环路L，由安培环路定理fB.d7 = B.ab= oab-i得圆筒内磁感应强度大小为：B= Hoi = μooR写成矢量式：B=R2.如图，一半径为R的带电塑料圆盘，其中有一半径为r的阴景部分均匀带正电荷，面电荷密度为+α，其余部分均匀带负电荷，面电荷密度为－α，当圆盘以角速度の旋转时，测得圆盘中心0点的磁感应强度为零，间R与r满足什么关系？解：带电圆盘转动时，可看作无数圆电流的磁场在0点的叠加。取半径为，宽为d的圆环，其上电流di=02元5d5.CoEds

由有磁介质时安培环路定律   =  内 d 0 H l I L   可得： H l H r I L  =  =  d 2   于是 r 处磁场强度大小为： r I H 2 = 又 B = H ，故 r 处磁感应强度大小为： r I B H    2 = = 。 三、计算题： 1．如图所示，一半径为 R 的均匀带电无限长直圆筒， 电荷面密度为  ，该筒以角速度  绕其轴线匀速旋 转，试求圆筒内部的磁感应强度。 解：带电圆筒旋转相当于圆筒表面有面电流，单位长度上电流为；    i = R  = R 2 2 与长直通电螺线管内磁场分布类似。圆筒内为均匀磁场， B  的方向与   一致（若  <0，则相 反）。圆筒外 B = 0  。作如图所示的安培环路 L，由安培环路定理： B l B ab ab i L  =  =   d 0   得圆筒内磁感应强度大小为： B = 0 i = 0 R 写成矢量式：      B = 0 R 2．如图，一半径为 R 的带电塑料圆盘，其中有一半径为 r 的阴影 部分均匀带正电荷，面电荷密度为 + ，其余部分均匀带负电荷， 面电荷密度为 − ，当圆盘以角速度  旋转时，测得圆盘中心 O 点的磁感应强度为零，问 R 与 r 满足什么关系？ 解：带电圆盘转动时，可看作无数圆电流的磁场在 O 点的叠加。 取半径为  ，宽为 d 的圆环，其上电流         d 2 di = 2 d  =   R  d O R r    R L a b d c i r L I I 

uodi它在中心0产生的磁感应强度为：dB=Hogad2正电荷部分产生的磁场为：B=Hocodooor负电荷部分产生的磁场为：B=oodg=μgoo(R-r)而题设B.=B，故得R-23.一线圈由半径为0.2m的1/4圆弧和相互垂直的二直线组成，通以区电流2A，把它放在磁感应强度为0.5T的均匀磁场中（磁感应强度B的方向如图所示)。求：（1）线圈平面与磁场垂直时，圆弧AB所受的磁力。（2）线圈平面与磁场成60°角时，线圈所受的磁力矩解：（1）在均勾磁场中，弦线AB所受的磁力与弧线B通一同样的电流所受的磁力杯由安培定律得：XFa=F=V2RIB=/2×0.2×2×0.5=0.283(N)方向与AB弧线垂直，与OB夹角为45°，如图所示。（2）线圈的磁矩：P,=IS=2×元×0.2n=2元x10-2nn与B夹角为(90°-60°)=30°，所受磁力大小为M = P.Bsin 300=2元×10-2×0.5×=1.57×10- (N·m)M的方向将驱使线圈法线π转向与B平行

它在中心 O 产生的磁感应强度为：      d 2 1 2 d d 0 0 = = i B 正电荷部分产生的磁场为： B r r  + = = 0 0 0 2 1 d 2 1      负电荷部分产生的磁场为： ( ) 2 1 d 2 1 0 0 B R r R r = = − −       而题设 B+ = B− ，故得 R=2 r 3．一线圈由半径为 0.2m 的 1 4 圆弧和相互垂直的二直线组成，通以 电流 2A ，把它放在磁感应强度为 0.5T 的均匀磁场中（磁感应强度 B  的方向如图所示）。求： （１）线圈平面与磁场垂直时，圆弧  AB 所受的磁力。 （２）线圈平面与磁场成 60 角时，线圈所受的磁力矩。 解：（１）在均匀磁场中，弦线 AB 所受的磁力与弧线  AB 通一同样的电流所受的磁力相等。 由安培定律得： F  = F = 2RIB = 2  0.2 2 0.5 = 0.283(N) AB AB 方向与  AB 弧线垂直，与 OB 夹角为 45 ，如图所示。 （２）线圈的磁矩： Pm IS n n n     2 2 0.2 2 10 4 1 2 − = =    =   n  与 B  夹角为 (90 − 60) = 30 ，所受磁力大小为 1.57 10 (N m) 2 1 2 10 0.5 sin 30 2 2 =   =    =  − −  M Pm B M  的方向将驱使线圈法线 n  转向与 B  平行 A B O B I  FAB  R B  o I B A