《大学物理学》课程作业习题（含解答）第13章作业题

13一8如图所示，一定量的空气，开始在状态A，其压强为2.0x105Pa，体积为2.0×10~3m3沿直线AB变化到状态B后，压强变为1.0×10-Pa，体积变为3.0×10=3m3，求此过程中气体所作的功。p/10°PaV10m题13-8图分析理想气体作功的表达式为W=Jp(V)dV.功的数值就等于p-V图中过程曲线下所对应的面积解 SABCD =1/2(BC +AD)xCDW =150J13一10一定量的空气，吸收了1.71×10J的热量，并保持在1.0×105Pa下膨胀，体积从1.0×102m3增加到1.5×10-2m3，问空气对外作了多少功？它的内能改变了多少？分析由于气体作等压膨胀，气体作功可直接由W=p(V2-Vi)求得取该空气为系统，根据热力学第一定律Q=AE+W可确定它的内能变化.在计算过程中要注意热量、功、内能的正负取值，解该空气等压膨胀，对外作功为W =p(V2-Vi)=5.0 ×102J其内能的改变为Q =NE +W=1.21×103J13一14如图所示，系统从状态A沿ABC变化到状态C的过程中，外界有326J的热量传递给系统，同时系统对外作功126J.当系统从状态C沿另一曲线CA返回到状态A时，外界对系统作功为52J，则此过程中系统是吸热还是放热？传递热量是多少？

13 －8 如图所示，一定量的空气，开始在状态A，其压强为2.0×105Pa，体积为2.0 ×10－3m3 ， 沿直线AB 变化到状态B后，压强变为1.0 ×105Pa，体积变为3.0 ×10－3m3 ，求此过程中气体 所作的功. 分析 理想气体作功的表达式为 ( )  W = p V dV .功的数值就等于p－V 图中过程曲线下所 对应的面积. 解 SABCD ＝1/2(BC ＋AD)×CD 故 W ＝150 J 13 －10 一定量的空气，吸收了1.71×103J的热量，并保持在1.0 ×105Pa下膨胀，体积从1.0×10 －2m3 增加到1.5×10－2m3 ，问空气对外作了多少功？ 它的内能改变了多少？ 分析 由于气体作等压膨胀，气体作功可直接由W ＝p(V2 －V1 )求得.取该空气为系统，根 据热力学第一定律Q ＝ΔE ＋W 可确定它的内能变化.在计算过程中要注意热量、功、内能 的正负取值. 解 该空气等压膨胀，对外作功为 W ＝p(V2－V1 )＝5.0 ×102J 其内能的改变为 Q ＝ΔE ＋W＝1.21 ×103J 13 －14 如图所示，系统从状态A沿ABC 变化到状态C的过程中，外界有326J的热量传递 给系统，同时系统对外作功126J.当系统从状态C沿另一曲线CA返回到状态A时，外界对系 统作功为52J，则此过程中系统是吸热还是放热？传递热量是多少？

题13-14图分析已知系统从状态C到状态A，外界对系统作功为WcA，如果再能知道此过程中内能的变化AEAC，则由热力学第一定律即可求得该过程中系统传递的热量QcA.由于理想气体的内能是状态（温度)的函数，利用题中给出的ABC过程吸热、作功的情况，由热力学第一定律即可求得由A至C过程中系统内能的变化△EAc，而AEAc=—△EAC，故可求得QcA：解，系统经ABC过程所吸收的热量及对外所作的功分别为QABC =326],WABC =126J则由热力学第一定律可得由A到C过程中系统内能的增量AEAC=QABC-WABC=2001由此可得从C到A，系统内能的增量为AEcA=200J从C到A，系统所吸收的热量为QcA =△EcA +WcA =-252J式中负号表示系统向外界放热252J.这里要说明的是由于CA是一未知过程，上述求出的放热是过程的总效果，而对其中每一微小过程来讲并不一定都是放热。13一15如图所示，一定量的理想气体经历ACB过程时吸热700J，则经历ACBDA过程时吸热又为多少？

分析 已知系统从状态C 到状态A，外界对系统作功为WCA ，如果再能知道此过程中内能 的变化ΔEAC ，则由热力学第一定律即可求得该过程中系统传递的热量QCA .由于理想气体的 内能是状态(温度)的函数，利用题中给出的ABC 过程吸热、作功的情况，由热力学第一定 律即可求得由A至C过程中系统内能的变化ΔEAC，而ΔEAC＝－ΔEAC ，故可求得QCA . 解 系统经ABC 过程所吸收的热量及对外所作的功分别为 QABC ＝326J， WABC ＝126J 则由热力学第一定律可得由A 到C 过程中系统内能的增量 ΔEAC＝QABC－WABC＝200J 由此可得从C 到A，系统内能的增量为 ΔECA＝－200J 从C 到A，系统所吸收的热量为 QCA ＝ΔECA ＋WCA ＝－252J 式中负号表示系统向外界放热252 J.这里要说明的是由于CA是一未知过程，上述求出的放热 是过程的总效果，而对其中每一微小过程来讲并不一定都是放热. 13 －15 如图所示，一定量的理想气体经历ACB过程时吸热700J，则经历ACBDA 过程时 吸热又为多少？

Ap/10°PaV/10m题13-15图分析从图中可见ACBDA过程是一个循环过程.由于理想气体系统经历一个循环的内能变化为零，故根据热力学第一定律，循环系统净吸热即为外界对系统所作的净功为了求得该循环过程中所作的功，可将ACBDA循环过程分成ACB、BD及DA三个过程讨论其中BD及DA分别为等体和等压过程，过程中所作的功按定义很容易求得：而ACB过程中所作的功可根据上题同样的方法利用热力学第一定律去求解由图中数据有pAVA=pBVB,则A、B两状态温度相同，故ACB过程内能的变化AEcAB=0，由热力学第一定律可得系统对外界作功WcAB =QcAB-△ECAB=QcAB =700在等体过程BD及等压过程DA中气体作功分别为Wep =J p(V)aV =0Wox =[ pdV= P(V,-V)=-1200 J则在循环过程ACBDA中系统所作的总功为W =WAcs +Wep +WDA =-500 J负号表示外界对系统作功.由热力学第一定律可得，系统在循环中吸收的总热量为Q=W=-500J负号表示在此过程中，热量传递的总效果为放热。13110.1kg的水蒸气自120℃加热升温到140℃，间(1)在等体过程中：(2)在等压过程中，各吸收了多少热量？根据实验测定，已知水蒸气的摩尔定压热容Cpm36.21Jmol1K-1，摩尔定容热容Cvm=27.82]mol1K-1

分析 从图中可见ACBDA过程是一个循环过程.由于理想气体系统经历一个循环的内能变 化为零，故根据热力学第一定律，循环系统净吸热即为外界对系统所作的净功.为了求得该 循环过程中所作的功，可将ACBDA循环过程分成ACB、BD及DA三个过程讨论.其中BD 及 DA分别为等体和等压过程，过程中所作的功按定义很容易求得；而ACB过程中所作的功可 根据上题同样的方法利用热力学第一定律去求. 解 由图中数据有pAVA ＝pBVB,则A、B两状态温度相同，故ACB过程内能的变化ΔECAB ＝ 0，由热力学第一定律可得系统对外界作功 WCAB ＝QCAB－ΔECAB＝QCAB ＝700J 在等体过程BD 及等压过程DA 中气体作功分别为 ( )  WBD = p V dV = 0 ( )  = d = − = −1200 J WDA p V PA V2 V1 则在循环过程ACBDA 中系统所作的总功为 500 J W =WACB +WBD +WDA = − 负号表示外界对系统作功.由热力学第一定律可得，系统在循环中吸收的总热量为 Q = W = −500 J 负号表示在此过程中，热量传递的总效果为放热. 13 －11 0.1kg 的水蒸气自120 ℃加热升温到140℃，问(1) 在等体过程中；(2) 在等压过程 中，各 吸收 了多 少热 量？ 根 据实 验测 定， 已知 水蒸 气的 摩尔 定压 热容Cp,m ＝ 36.21J·mol-1·K-1，摩尔定容热容CV,m ＝27.82J·mol-1·K-1

分析由量热学知热量的计算公式为Q=OC.,AT.按热力学第一定律，在等体过程中，Qv=△E=vCv,mAT；在等压过程中，Q,=J pdV+AE=OCpmAT.解(1）在等体过程中吸收的热量为Qv=AE=CvmAT=3.1x10 (2) 在等压过程中吸收的热量为2,=J dV+E=Cm(-)=4.0×10 ]13-17空气由压强为1.52×105Pa，体积为5.0×10~3m3，等温膨胀到压强为1.01×105Pa,然后再经等压压缩到原来的体积.试计算空气所作的功解，空气在等温膨胀过程中所作的功为W=RT,n(V/V)=Pn(p/p.)空气在等压压缩过程中所作的功为W=J pdV=p(V,-)利用等温过程关系p1V1=p2V2，则空气在整个过程中所作的功为W =W, +W, = pVn(p/ / p:)+ p:V-pV= 55.7J13-19将体积为1.0×10m、压强为1.01×10-Pa的氢气绝热压缩，使其体积变为2.0×10-5m3，求压缩过程中气体所作的功（氢气的摩尔定压热容与摩尔定容热容比值y=1.41)分析可采用题13-13中气体作功的两种计算方法:(1）气体作功可由积分W=JpdV求解，其中函数p(V)可通过绝热过程方程pV=C得出(2)因为过程是绝热的，故Q=0，因此，有W=一AE：而系统内能的变化可由系统的始末状态求出。解根据上述分析，这里采用方法(1)求解,方法(2)留给读者试解.设p、V分别为绝热过程中任一状态的压强和体积，则由PV=pV7得p=pVV-氢气绝热压缩作功为

分析 由量热学知热量的计算公式为 Q = vCmΔT .按热力学第一定律，在等体过程中， QV = ΔE = vCV, mΔT ；在等压过程中， Qp = pdV + ΔE = vCp,mΔT  . 解 (1) 在等体过程中吸收的热量为 Δ Δ 3.1 10 J 3 V = = CV,m T =  M m Q E (2) 在等压过程中吸收的热量为 d Δ ( ) 4.0 10 J 3 p = + = p,m 2 − 1 =   C T T M m Q p V E 13 －17 空气由压强为1.52×105 Pa，体积为5.0×10－3m3 ，等温膨胀到压强为1.01×105 Pa， 然后再经等压压缩到原来的体积.试计算空气所作的功. 解 空气在等温膨胀过程中所作的功为 ( ) ( ) T 1 2 1 1 1 1 2 RT ln V /V pV ln p / p M m W = = 空气在等压压缩过程中所作的功为 ( )  W = pdV = p V2 −V1 利用等温过程关系p1 V1 ＝p2 V2 ，则空气在整个过程中所作的功为 ( ) 55.7 J ln / 1 1 1 2 2 1 1 1 = W =Wp +WT = pV p p + p V − pV 13 －19 将体积为1.0 ×10-4m3 、压强为1.01×105Pa 的氢气绝热压缩，使其体积变为2.0 ×10-5 m3 ，求压缩过程中气体所作的功.(氢气的摩尔定压热容与摩尔定容热容比值γ＝1.41) 分析 可采用题13－13 中气体作功的两种计算方法.(1) 气体作功可由积分 W pdV  = 求 解，其中函数p(V)可通过绝热过程方程 pV C  = 得出.(2)因为过程是绝热的，故Q＝0，因 此，有W＝－ΔE；而系统内能的变化可由系统的始末状态求出. 解 根据上述分析，这里采用方法(1)求解,方法(2)留给读者试解.设p、V分别为绝热过程中 任一状态的压强和体积，则由 γ γ p1V1 = pV 得 γ γ p pV V − = 1 1 氢气绝热压缩作功为

VW=-23.0 JW=[ -" d=V13—21 1mol氢气在温度为300K，体积为0.025m3的状态下，经过(1)等压膨胀，(2)等温膨胀，(3)绝热膨胀.气体的体积都变为原来的两倍.试分别计算这三种过程中氢气对外作的功以及吸收的热量。Pf(2)340.05V0.025题13-21图分析这三个过程是教材中重点讨论的过程在p一V图上，它们的过程曲线如图所示.由图可知过程(1）作功最多，过程（3）作功最少.温度TB>Tc>TD，而过程(3）是绝热过程因此过程(1)和(2)均吸热，且过程(1)吸热多.具体计算时只需直接代有关公式即可解 (1)等压膨胀()()2492,=W,+=C.(-)=T,,=8.7310 (2) 等温膨胀W,=0RTlnVe/V,= RT, n2=1.73×10 J对等温过程AE=0，所以Q,=W,=1.73×10(3) 绝热膨胀TD=TA(VA / VD)1=300×(0.5)04=227.4K对绝热过程.=0，则有

23.0 J 1 d d 1 2 1 2 1 1 1 2 1  = −       −      − = = =   − V V V V γ p W p V pV V V V V γ γ 13 －21 1mol 氢气在温度为300Ｋ，体积为0.025m3 的状态下，经过(1)等压膨胀，(2)等温 膨胀，(3)绝热膨胀.气体的体积都变为原来的两倍.试分别计算这三种过程中氢气对外作的功 以及吸收的热量. 分析 这三个过程是教材中重点讨论的过程.在p －V 图上，它们的过程曲线如图所示.由图 可知过程(1 ) 作功最多， 过程( 3 ) 作功最少.温度TB ＞TC ＞TD ，而过程(3) 是绝热过程， 因此过程(1)和(2)均吸热，且过程(1)吸热多.具体计算时只需直接代有关公式即可. 解 (1) 等压膨胀 ( ) ( ) 2.49 10 J 3 = − = B − A = A =  A A p A B A V V RT V RT W p V V v ( ) 8.73 10 J 2 7 3 p = p + = p,m B − A = p,m A = TA =  R Q W ΔE vC T T vC T (2) 等温膨胀 / ln 2 1.73 10 J 3 WT = vRTlnVC VA = RTA =  对等温过程ΔE＝0，所以 1.73 10 J 3 QT =WT =  (3) 绝热膨胀 TD＝TA (VA ／VD )γ－1＝300 ×(0.5)0.4＝227.4Ｋ 对绝热过程 a Q = 0 ，则有

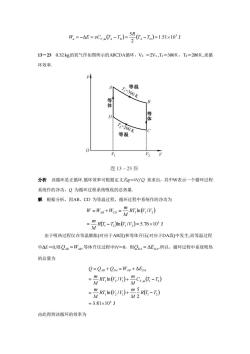
W,=-AE = 0Cv(T,-T)- R(T,-T,)=1.51×10′ J13-230.32kg的氧气作如图所示的ABCDA循环，V2=2V1,Ti=300K，T2=200K,求循环效率。pA等温V2题13-23图分析该循环是正循环.循环效率可根据定义式=W/Q来求出，其中W表示一个循环过程系统作的净功，Q为循环过程系统吸收的总热量解根据分析，因AB、CD为等温过程，循环过程中系统作的净功为W=Wan +Wcp =" RT,in(V/V)=R(T-T,)n(V/V)=5.76×103 JA由于吸热过程仅在等温膨胀(对应于AB段)和等体升压(对应于DA段)中发生,而等温过程中AE=0,则QAB=WAB:等体升压过程中W=0，则QDA=AEDA,所以，循环过程中系统吸热的总量为Q=QAB+QDA=WAB+AEDA="RT,n(V/V)+Cym(T-T.)--RrT (/)+R(C-T)=3.81×10*J由此得到该循环的效率为

( ) ( ) 1.51 10 J 2 5 Δ 3 a = − = V ,m A − D = TA −TD =  R W E vC T T 13－23 0.32 kg的氧气作如图所示的ABCDA循环，V2 ＝2V1 ,T1＝300Ｋ，T2＝200Ｋ,求循 环效率. 分析 该循环是正循环.循环效率可根据定义式η＝W/Q 来求出，其中W表示一个循环过程 系统作的净功，Q 为循环过程系统吸收的总热量. 解 根据分析，因AB、CD 为等温过程，循环过程中系统作的净功为 ( ) ( )ln( / ) 5.76 10 J ln / 3 1 2 1 2 1 1 2 = − =  = + = R T T V V M m RT V V M m W WAB WCD 由于吸热过程仅在等温膨胀(对应于AB段)和等体升压(对应于DA段)中发生,而等温过程 中ΔE＝0,则 QAB =WAB .等体升压过程中W＝0，则 QDA = ΔEDA ,所以，循环过程中系统吸热 的总量为 ( ) ( ) ( ) ( ) 3.81 10 J 2 5 ln / ln / Δ 4 1 2 1 1 2 1 2 1 , 1 2 =  = + − = + − = + = + R T T M m RT V V M m C T T M m RT V V M m Q Q Q W E V m AB DA AB DA 由此得到该循环的效率为

n=W/Q=15%13-24图（a)是某单原子理想气体循环过程的V-T图，图中Ve=2VA.试间：(）图中所示循环是代表制冷机还是热机？(2）如是正循环(热机循环)，求出其循环效率。A(a)(b)题13-24图分析以正、逆循环来区分热机和制冷机是针对p一V图中循环曲线行进方向而言的.因此，对图(a)中的循环进行分析时，一般要先将其转换为p一V图.转换方法主要是通过找每一过程的特殊点，并利用理想气体物态方程来完成.由图（a)可以看出，BC为等体降温过程，CA为等温压缩过程：而对AB过程的分析，可以依据图中直线过原点来判别.其直线方程为V：CT，C为常数.将其与理想气体物态方程pV=m/MRT比较可知该过程为等压膨胀过程(注意：如果直线不过原点，就不是等压过程).这样，就可得出p一V图中的过程曲线，并可判别是正循环(热机循环)还是逆循环(制冷机循环)，再参考题13-23的方法求出循环效率解（I）根据分析，将V-T图转换为相应的p一V图，如图(b)所示.图中曲线行进方向是正循环，即为热机循环。(2)根据得到的p-V图可知，AB为等压膨胀过程，为吸热过程.BC为等体降压过程，CA为等温压缩过程，均为放热过程.故系统在循环过程中吸收和放出的热量分别为9 =C.m(T,-T.)0, ="Cvm(Tg-T)+"RT,In(Ve/V)CA为等温线，有TA=Tc；AB为等压线，且因Vc=2VA，则有TA=TB/2.对单原子理想气体，其摩尔定压热容Cp.m=5R/2，摩尔定容热容Cv.m=3R/2.故循环效率为n=1-0. /Q =1-[T, +T, n2 /(6T,/2)=1-(3+2in2)/5=12/3

η = W /Q =15% 13 －24 图(ａ)是某单原子理想气体循环过程的V－T 图，图中VC ＝2VA .试问：(1) 图中 所示循环是代表制冷机还是热机？ (2) 如是正循环(热机循环)，求出其循环效率. 分析 以正、逆循环来区分热机和制冷机是针对p－V 图中循环曲线行进方向而言的.因此， 对图(ａ)中的循环进行分析时，一般要先将其转换为p－V图.转换方法主要是通过找每一过 程的特殊点，并利用理想气体物态方程来完成.由图(ａ)可以看出，BC 为等体降温过程，CA 为等温压缩过程；而对AB 过程的分析，可以依据图中直线过原点来判别.其直线方程为V ＝ CT，C 为常数.将其与理想气体物态方程pV ＝m/MRT 比较可知该过程为等压膨胀过程(注 意：如果直线不过原点，就不是等压过程).这样，就可得出p－V 图中的过程曲线，并可判 别是正循环(热机循环)还是逆循环(制冷机循环)，再参考题13－23的方法求出循环效率. 解 (1) 根据分析，将V－T 图转换为相应的p－V图，如图(ｂ)所示.图中曲线行进方向是正 循环，即为热机循环. (2) 根据得到的p－V 图可知，AB 为等压膨胀过程，为吸热过程.BC 为等体降压过程，CA 为等温压缩过程，均为放热过程.故系统在循环过程中吸收和放出的热量分别为 ( ) Cp m TB TA M m Q1 = , − ( ) ( ) V m B A RTA VC VA M m C T T M m Q ln / 2 = , − + CA 为等温线，有TA＝TC ；AB 为等压线，且因VC＝2VA ，则有TA ＝TB /2.对单原子理 想气体，其摩尔定压热容Cp，m ＝5R/2，摩尔定容热容CV，m ＝3R/2.故循环效率为 ln 2 /(5 / 2) 1 (3 2ln 2)/5 12/3 3 2 1 2 / 1 1 = − + =       η = − Q Q = − TA + TA TA

一卡诺热机的低温热源温度为7℃，效率为40%，若要将其效率提高到50%，问高13—25温热源的温度需提高多少？解，设高温热源的温度分别为T'、T"则有n=1-T/T'，n"=1-T/T"其中T2为低温热源温度.由上述两式可得高温热源需提高的温度为 =93.3 KAT = T'- T'=[13一28有一以理想气体为工作物质的热机，其循环如图所示，试证明热(v/v)-1n=1-(p. / p.)-1分析该热机由三个过程组成，图中AB是绝热过程，BC是等压压缩过程，CA是等体升压过程.其中CA过程系统吸热，BC过程系统放热.本题可从效率定义m=1-Q/Q,=1-QBc/Qca出发,利用热力学第一定律和等体、等压方程以及=Cpm样Cvm的关系来证明.PC题13-28图证该热机循环的效率为m=1-Q,/Q, =1-Qc /Oc其中QBC =m/MCpm(Tc-TB)，QcA=m/MCv.m(TA-Tc)，则上式可写为

13 －25 一卡诺热机的低温热源温度为7℃，效率为40％，若要将其效率提高到50％，问高 温热源的温度需提高多少？ 解 设高温热源的温度分别为 T1  、T1  ,则有 2 1 η  =1−T /T， 2 1 η  =1−T /T 其中T2 为低温热源温度.由上述两式可得高温热源需提高的温度为 93.3 K 1 1 1 1 Δ 1 1 2 =         −  − −  = −  = T η η T T T 13 －28 有一以理想气体为工作物质的热机，其循环如图所示，试证明热 ( ) ( / ) 1 / 1 1 1 2 1 2 − − = − p p V V η γ 分析 该热机由三个过程组成，图中AB是绝热过程，BC是等压压缩过程，CA是等体升压 过 程 . 其 中 CA 过 程 系 统 吸 热 ， BC 过 程 系 统 放 热 . 本 题 可 从 效 率 定 义 η Q Q QBC QCA 1 / 1 / = − 2 1 = − 出发,利用热力学第一定律和等体、等压方程以及γ＝Cp,m 桙 CV,m的关系来证明. 证 该热机循环的效率为 η Q Q QBC QCA 1 / 1 / = − 2 1 = − 其中QBC ＝m/MCp,m (TC－TB )，QCA ＝m/MCV,m (TA－TC )，则上式可写为

[Te-Tal =1-2T,/Tc-1-"TA/Te-1T -1在等压过程BC和等体过程CA中分别有TB/V1=Tc/V2,TA/P1=Tc/P2,代入上式得(v//v,)-1n=1- (0/p)-113—33物质的量为v的理想气体，其摩尔定容热容Cvm=3R/2，从状态A(pA，VA，TA）分别经如图所示的ADB过程和ACB过程，到达状态B(pB，VB，TB).试问在这两个过程中气体的嫡变各为多少？图中AD为等温线。plPD=PB2.43Ve-VB题13-33图分析摘是热力学的状态函数，状态A与B之间的摘变ΛSAB不会因路径的不同而改变.此外，ADB与ACB过程均由两个子过程组成.总的摘变应等于各子过程变之和，即ASAB=ASAD +ASDe或ASAs=ASAc+AScB*解 (1) ADB过程的嫡变为ASAB=ASAD+ASDE=I'do,/T+J'do,/ T(1)=J'dW,/T+J'oCp.mdT/T= URIn(V,/VA)+oCp.m In(T /T,)在等温过程AD中，有TD=TA；等压过程DB中，有VB/TB=VD/TD：而Cpm=Cv,m+R,故式(1)可改写为

/ 1 / 1 1 1 − − = − − − = − A C B C A C C B T T T T γ T T T T η γ 在等压过程BC 和等体过程CA 中分别有TB/V1 ＝TC/V2,TA/P1 ＝TC /P2,代入上式得 ( ) ( / ) 1 / 1 1 1 2 1 2 − − = − p p V V η γ 13 －33 物质的量为ν的理想气体，其摩尔定容热容CV,m＝3R/2，从状态A(pA，VA，TA ) 分别经如图所示的ADB过程和ACB过程，到达状态B(pB，VB，TB).试问在这两个过程中气体 的熵变各为多少？ 图中AD为等温线. 分析 熵是热力学的状态函数，状态A与B之间的熵变ΔSAB不会因路径的不同而改变.此外， ADB 与 ACB 过程 均 由 两个 子 过 程组 成. 总 的熵 变 应 等于 各 子 过程 熵 变 之和 ， 即 ΔSAB = ΔSAD +ΔSDB 或 ΔSAB = ΔSAC + ΔSCB . 解 (1) ADB过程的熵变为 ( ) ( ) D A p,m B D B D D A T B D P D A T AB AD DB V V C T T W T C T T Q T Q T S S S ln / ln / d / d / d / d / Δ Δ Δ p,m vR v v = + = + = + = +     (1) 在等温过程AD中，有TD＝TA；等压过程DB中，有VB /TB＝VD /TD ；而Cp，m＝CV，m ＋R， 故式(1)可改写为

ASADs = ORIn(T,Vg/T,V.)+0Cpm Ih(T, /V)=ORIn(Vs/V)+号oRIn(T /V))(2) ACB 过程的筛变为ASAcn = I'dOT = ASAc +AScs(2)=0Cpm n(T /V)+ VCvm In(Tg/T.)利用Vc=VB、PC =pA、Tc /Ve=TA /VA及Ts/pB=Tc/pc，则式(2)可写为ASAcB =(Cvm + R)n(Vg/V)+0ln(p / pa)= ORIn(V./V)+OCvm n(PVe/ pAV)=ORIn(V./V)+号ORIn(T./V))通过上述计算可看出，虽然ADB及ACB两过程不同，但熵变相同因此，在计算嫡变时，可选取比较容易计算的途径进行13一34有一体积为2.0×10-m3的绝热容器，用一隔板将其分为两部分，如图所示.开始时在左边（体积V1=5.0×10-3m)一侧充有1mol理想气体，右边一侧为真空.现打开隔板让气体自由膨胀而充满整个容器，求熵变.TV题13-34图分析 在求解本随时、严往癌AS=)%α的适用条件.在绝热自由膨胀过程中，dQ=0,若仍运用上式计算摘变，必然有△S=0.显然，这是错误的结果由于摘是状态的单值函数当初态与末态不同时，熵变不应为零.出现上述错误的原因就是忽视了公式的适用条件AS="只适用于可道过程，而自由膨胀过程是不可道的.因此，在求解不可道过程的熵变时，通常需要在初态与末态之间设计一个可逆过程，然后再按可逆过程熵变的积分式进

( ) ( ) ( ) ( ) B A B A ADB D B B A p,m B A V V T V S T V T V C T V ln / 2 3 ln / Δ ln / ln / vR vR vR v = + = + (2) ACB 过程的熵变为 ( ) ( ) p,m C A V,m B C AC CB B A ACB C T V C T T S Q/T S S ln / ln / Δ d Δ Δ = v + v = = +  (2) 利用VC＝VB、pC ＝pA、TC /VC＝TA /VA 及TB /pB＝TC/pC，则式(2)可写为 ( ) ( ) ( ) ( ) ( ) ( ) ( ) B A B A B A V,m B B A A ACB V,m B A B A V V T V V V C p V p V S C R V V p p ln / 2 3 ln / ln / ln / Δ ln / ln / vR vR vR v v v = + = + = + + 通过上述计算可看出，虽然ADB及ACB两过程不同，但熵变相同.因此，在计算熵变时， 可选取比较容易计算的途径进行. 13 －34 有一体积为2.0 ×10-2m3的绝热容器，用一隔板将其分为两部分，如图所示.开始时 在左边(体积V1 ＝5.0 ×10-3m3)一侧充有1mol理想气体，右边一侧为真空.现打开隔板让气体 自由膨胀而充满整个容器，求熵变. 分析 在求解本题时，要注意  = B A T Q S d Δ 的适用条件.在绝热自由膨胀过程中，dQ ＝0， 若仍运用上式计算熵变，必然有ΔS ＝0.显然，这是错误的结果.由于熵是状态的单值函数， 当初态与末态不同时，熵变不应为零.出现上述错误的原因就是忽视了公式的适用条件.  = B A T Q S d Δ 只适用于可逆过程，而自由膨胀过程是不可逆的.因此，在求解不可逆过程的 熵变时，通常需要在初态与末态之间设计一个可逆过程，然后再按可逆过程熵变的积分式进