《信号与系统》课程教学资源(习题解答)第八章 状态方程与状态变量分析法

CIEECAU状态方程与状态变量分析法第八章本章重点(1)系统状态方程的建立,根据系统的微分或差分方程、系统的方框图、流图或电路图来建立系统的状态方程。(2)利用系统的状态方程求系统的转移函数及系统的微分或差分方程(3)利用状态方程中的A矩阵求连续系统状态转移矩阵()=e,或利用(),求A矩阵。(4)连续系统状态方程及输出方程的时域解法与变换域解法。(5)利用状态方程中的A矩阵求离散系统状态转移矩阵$(n)=A",或利用(n)求A矩a(6)离散系统状态方程及输出方程的时域解法与变换域解法。(7)系统完全可控与完全可观测的充要条件。例8.1试分别用串联结构和并联结构形式实现下式的状态方程和输出方程4(s +2.5)H(s) :(s+1)(s+2)(s+3)解(a)串联结构实现时,可按下式进行:1.$+2.5.4H(s)=1$+2$+3可以画出,实现转移函数为as+a+a,s-l+b.的流图如图右所示。由此可画出实现-beH(s)串联形式的流图如下图所示。设积分器的输出为状态变量,可以得出状态变量方程为[元=-3元+2.5元+(2-22)含=-22+13=-n+e
CIEE CAU 第八章 状态方程与状态变量分析法 本章重点 (1)系统状态方程的建立,根据系统的微分或差分方程、系统的方框图、流图或电路 图来建立系统的状态方程。 (2)利用系统的状态方程求系统的转移函数及系统的微分或差分方程。 (3)利用状态方程中的 A矩阵求连续系统状态转移矩阵 ( ) At φ t e = ,或利用φ( )t ,求 A 矩阵。 (4)连续系统状态方程及输出方程的时域解法与变换域解法。 (5)利用状态方程中的 A矩阵求离散系统状态转移矩阵 ( ) n φ n A = ,或利用φ( ) n 求 A矩 阵。 (6)离散系统状态方程及输出方程的时域解法与变换域解法。 (7)系统完全可控与完全可观测的充要条件。 例 8.1 试分别用串联结构和并联结构形式实现下式的状态方程和输出方程: 4( 2.5) ( ) ( 1)( 2)( 3) s H s ss s + = + + + 解 (a)串联结构实现时,可按下式进行: 1 2.5 4 ( ) 123 s H s s s s + =⋅ ⋅ + + + 可以画出,实现转移函数为 1 1 0 10 1 0 0 1 as a a a s s b bs − − + + = + + 的流图如图右所示。由此可画出实现 H s( ) 串联形式的流图如下图所示。设积分 器的输出为状态变量,可以得出状态变量方 程为 1 1 23 2 2 23 3 3 3 2.5 ( 2 ) 2 e λ λ λλ λ λ λλ λ λ =− + + − =− + =− + & & & 1 a 0 −b 1 s− 0 a 图 10.2.1

2.5输出方程为4表示成矩阵形式为输出方程为Mr=[4 0 0]|2[(b)并联结构实现时,可将H(s)展成部分分式,即4(s +2.5)H(0)=(3+1G+2)($+3)$+1++2+$+3其流图实现形式如下图所示。选积分器的输出为状态变量,可以写出状态方程为i =-n+ei =-21 +eig=-31, +e而输出方程为r=34-2h -2表示成矩阵形式为输出方程为
CIEE CAU 输出方程为 1 r = 4λ 表示成矩阵形式为 1 1 2 2 3 3 3 0.5 1 0 0 21 0 00 1 1 e λ λ λ λ λ λ − =− + − & & & 输出方程为 [ ] 1 2 3 r 400 λ λ λ = (b)并联结构实现时,可将 H s( ) 展成部分分式,即 4( 2.5) ( ) ( 1)( 2)( 3) s H s ss s + = + + + 3 21 ss s 123 − − =+ + + + + 其流图实现形式如下图所示。选积分器的输出为状态变量,可以写出状态方程为 1 1 2 2 3 3 2 3 e e e λ λ λ λ λ λ =− + = − + = − + & & & 而输出方程为 1 23 r = 3 2 λ − − λ λ 表示成矩阵形式为 1 1 2 2 3 3 10 0 1 0 20 1 00 3 1 e λ λ λ λ λ λ − =− + − & & & 输出方程为 1 s− 0 a -1 -2 -3 2.5 λ3 λ2 λ1 1 s− 1 s − e 图 10.2.2
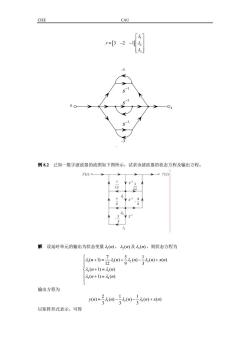
CIEE=13例8.2已知一数字滤波器的流图如下图所示,试求该滤波器的状态方程及输出方程。x(2)a解设延时单元的输出为状态变量(n),2(n)及(n),则状态方程为[(n+1)=号(m)+号(m)-16(n)+x(n)2(n+1)=2(n)(n+1)=(n)输出方程为(n)=(n)-2(n)-2(m)+ (n)以矩阵形式表示,可得
CIEE CAU [ ] 1 2 3 r 321 λ λ λ = −− 1 s− 1 s− 1 s− -1 -3 e r 图 10.2.3 例 8.2 已知一数字滤波器的流图如下图所示,试求该滤波器的状态方程及输出方程。 图 10.4 解 设延时单元的输出为状态变量 1 λ ( ) n , 2 λ ( ) n 及 3 λ ( ) n ,则状态方程为 1 123 2 1 3 2 7 51 ( 1) ( ) ( ) ( ) ( ) 12 9 3 ( 1) ( ) ( 1) ( ) n n n n xn n n n n λ λλλ λ λ λ λ += + − + + = + = 输出方程为 123 211 () () () () () 333 yn n n n xn =−−+ λλλ 以矩阵形式表示,可得

CIEE2(n+1)2(n+1) =02(n+1) |M(n)(n)2(n)+x(n1a(n)例8.3已知^-[% ]试求状态转移矩阵$(n)。解状态转移矩阵(n)的 z变换为=[(0(m)]-[(=I-A)"]题中已给定A,故--[3 2][Z-51ad;(ZI - A)=1-6Zdet(ZI - A)=(Z-2)(Z-3)(1-)"- (ZI-A)"det(ZI-A)Z-=(z-2)(2-3) (z-2)(2-3)[(Z-2)(Z-3) (Z-2)(Z-3)]=[0()] [(Z - A)"2]z2-5(Z-2)(Z-3)(Z-2)(Z-3)67[(Z-2)(Z-3) (Z-2)(Z-3)]可得状态转移矩阵3·2"-2.3"+(n)=-[(z1 - A)"z]-3.2#+1 -2.3n+l-2n+1
CIEE CAU 1 1 2 2 3 3 75 1 ( 1) ( ) 12 9 3 1 ( 1) 1 0 0 ( ) 0 ( ) ( 1) ( ) 01 0 0 n n n n xn n n λ λ λ λ λ λ − + += + + 1 2 3 ( ) 211 () () () 333 ( ) n yn n xn n λ λ λ = −− + 例 8.3 已知 0 1 6 5 A = − 试求状态转移矩阵φ( ) n 。 解 状态转移矩阵φ( ) n 的 z 变换为 [ ] ( ) 1 z n zI A z φ( ) − = − 题中已给定 A,故 1 6 5 Z ZI A Z − − = − ( ) 5 1 6 Z adj ZI A Z − − = − det ( 2)( 3) (ZI A Z Z −=− − ) ( ) ( ) ( ) 1 det adj ZI A zI A ZI A − − − = − 5 1 ( 2)( 3) ( 2)( 3) 6 ( 2)( 3) ( 2)( 3) Z ZZ ZZ Z ZZ ZZ − −− −− = − −− −− [ ] ( ) 1 z n ZI A Z φ( ) − = − 2 2 5 ( 2)( 3) ( 2)( 3) 6 ( 2)( 3) ( 2)( 3) ZZ Z ZZ ZZ Z Z ZZ ZZ − −− −− = − −− −− 可得状态转移矩阵 ( ) 1 1 1 1 11 32 23 2 3 ( ) 32 23 2 3 n n nn n n nn φ n z ZI A Z − − + + ++ ⋅ −⋅ − + = −= ⋅ −⋅ − +

CIEECAU例8.4已知某系统的状态转移矩阵为()=[e(cos +sin)-2e"'sinte'sinte-'(cost- sint)]试求矩阵A。解利用状态转移矩阵的时间微分,即l - el-- d故He-(cost +sin)(-2e' sint)A=%(0ge'sint%e-(cos-sin)-2e"sint2e'sint-2e' cos/[-e'sint+e' cost-2e'cost-{3例8.5某连续时间系统的状态方程和输出方程为[][ 2[(][ e0][-[]r[@+e([ -(] e(]初始状态为[2(0"]_[1 1[e(0]-[e(0)][(0)]-[-1]e2(0)][8(0)]求状态变量和输出变量。解(1)求状态转移矩阵()。已知-[6 ]-4-[0 2]系统的特征方程为sI - A|=(s-1)(s +1)= 0可求得系统的特征根为α, =1,α, =-1于是
CIEE CAU 例 8.4 已知某系统的状态转移矩阵为 (cos sin ) 2 sin ( ) sin (cos sin ) t t t t e t t et t et e t t φ − − − − + − = − 试求矩阵 A。 解 利用状态转移矩阵的时间微分,即 0 0 At At t t d e Ae AI A dt = = = = = 故 ( ) 0 (cos sin ) 2 sin ( ) sin (cos sin ) t t t t t d d e t t et d dt dt A t dt d d et e t t dt dt φ − − = − − + − = = − 0 2 sin 2 sin 2 cos sin cos 2 cos t tt tt t t e t e te t e te t e t − −− −− − = − − = −+ − 0 2 1 2 − = − 例 8.5 某连续时间系统的状态方程和输出方程为 1 11 2 2 2 () () () 1 2 01 ( ) 0 1 10 () () t t et t et t λ λ λ λ = + − & & 1 11 2 22 () () () 1 1 10 () () () 0 1 10 rt t et rt t et λ λ = + − 初始状态为 1 1 1 1 2 2 (0 ) ( ) 1 () ; (0 ) 1 () ( ) e t t e t t λ ε λ δ − − = = − 求状态变量和输出变量。 解 (1)求状态转移矩阵φ( )t 。已知 [ ] 12 1 2 01 0 1 s A sI A s − − = −= − + , 系统的特征方程为 sI A s s − =− += ( 1)( 1) 0 可求得系统的特征根为 1 2 α =1, 1 α = − 于是

CAUCIE[e=C,+C,e"=C,-C,可解得C=(e'+").G-('-e')因此p(t)=e =C,I+C,A-(e' +e')++(e' -e')I(e' +e')-}(e' -e'")0-6](2)求状态变量。(t)= p(t)a(0-l)+ (t)B*e(1)于是[8]6 16 18 88]-[][2-] 20式中第一项是零输入解,第二项是零状态解,其完全解为2(0)]_[2e' +e -2t≥0[2()]1-(3)求输出变量。[81-6 1281- 8128]-{ [][-][][8][3]-8]
CIEE CAU 0 1 0 1 t t eCC e CC − = + = − 可解得 0 1 1 1 ( ), ( ) 2 2 tt tt C eeC ee − − =+ =− 因此 0 1 ( ) At φ t e CI CA == + 1 1 ( )( ) 2 2 1 1 0 ( )( ) 2 2 tt tt tt tt tt ee ee ee ee ee −− − − − ++ − − = +− − ( ) 0 tt t t eee t e φ − − − = (2)求状态变量。 1 λ φλ φ ( ) ( ) (0 ) ( ) ( ) t t tB et − = +∗ 于是 1 2 ( ) 1 0 1 () ( ) 0 0 1 1 0 () tt t tt t t t t eee eee t t e e t λ ε λ δ − − − − − − =+ ∗ − ( ) () () ( ) t tt t t t e ee te t e e t ε δ ε − − − − ∗ +∗ = + − ∗ 2 2 , 0 1 t tt t t e ee t e e − − − + − =+ ≥ − − 式中第一项是零输入解,第二项是零状态解,其完全解为 1 2 ( ) 2 2 , 0 ( ) 1 t t t t e e t t e λ λ − − + − = ≥ − (3)求输出变量。 1 1 2 2 () () 1 1 1 0 () () () 0 1 1 0 () rt t t rt t t λ ε λ δ = + − 1 1 () 2 2 0 1 () 1 t tt t t e ee t e e t ε δ − − − + − = ++ − − − 0 1 2 1 1 1 t t t e e e − − − =+ + − +

CAUCIEE-[8]1[9] 20第一项是零输入响应是零状态响应,完全响应光r(t)]-[2e]r(0/=例8.6已知一线性非时变系统在零输入条件下,(0-)=2(t):时,a(0)=[2(0-1)=试求(a)状态转移矩阵t)b)相应的A矩险解(a)在零输入条件下,在任意时刻t的状态由状态转移矩阵决定,根据(10-16)式,有2() =(0)2(0-)于是[] 0[] [] 0[]把上面两式合在一起,可得[ 2]3]由此可得[ 2 3][]于是o ]e-(b) 由
CIEE CAU 0 2 , 0 t t t e t e e − − =+ ≥ 第一项是零输入响应,第二项是零状态响应,完全响应为 1 2 ( ) 2 , 0 ( ) t t r t e t r t e− = ≥ 例 8.6 已知一线性非时变系统在零输入条件下,当 1 1 (0 ) 1 λ − = − 时, 2 2 ( ) t t e t e λ − − = − 1 2 (0 ) 1 λ − = − 时, 2 ( ) t t e t e λ − − = − 试求 (a)状态转移矩阵φ( )t (b)相应的 A 矩阵 解 (a) 在零输入条件下,在任意时刻 t 的状态由状态转移矩阵 决定,根据(10-16) 式,有 1 λ φλ ( ) ( ) (0 ) t t − = 于是 2 2 1 ( ) 1 t t e t e φ − − = − − , 2 2 ( ) 1 t t e t e φ − − = − − 把上面两式合在一起,可得 2 2 2 1 2 ( ) 1 1 t t t t e e t e e φ − − − − = − − − − 由此可得 1 2 2 2 1 2 ( ) 1 1 t t t t e e t e e φ − − − − − = − − − − 2 2 2 1 2 1 1 t t t t e e e e − − − − − − = − − 于是 2 2 2 2 2 22 ( ) 2 tt t t tt tt ee e e t ee ee φ −− − − −− −− − − = −− − (b)由

CAUCIEE[2e-e- 2e--2e-(s1 -A) = [(0)] =2-e-1 -e- 2e-1 -et22$+1 $+2 $+1'$+2[s+2'$+1 $+2/$+1s+3 2(s+1)(s+2)[ -1]s+3 2sI 4=(s+1)(s +2)L-1s(s+ 1)(s+2)[s+3s+21 $+3]4=sl-[: -2]-[0 -2][1 s+3]-[-1 -3]例8.7已知一连续系统的状态方程与输出方程为[i(1)=-42(0)+2()+e(0)[i(0)=-32,(t)+e(t)r(0)=4(0)试求(a)系统的微分方程表示。(b)若输入e(t)=ε(t)时,r0-(+-8)a)求系统的起始状态 (0-)解(a)将r(l)=()代入()表示式,可得dr0 = -4r(0)+2(0+(0)由于题中给定系统有两个积分器,因而可用二阶微分方程表示,将上式两边求导,可得Sr =-42r0+(0)+de0dtdt将题中给定的()表示式代入后,可得4r0+4%r0)+3r()-de0 +e(0)(b)求转移函数矩阵H(s)=C(s/ -A)"B+D
CIEE CAU ( ) [ ] ( )( ) 2 2 1 2 2 1 2 22 ( ) 2 2122 1212 1121 2121 1 3 2 1 2 1 tt t t tt tt ee e e sI A t ee ee ss ss s ss s s s s s ξφ ξ −− − − − −− −− − − − −= = −− − − − ++ ++ = − − + ++ + + = + + − 1 3 2 ( 1)( 2) 1 s sI A s s s − + −=+ + − 2 ( 1)( 2) 2 3 2 1 3 s s s s s s + + − = + + + 2 02 1 3 13 s A sI s − − =− = + − − 例 8.7 已知一连续系统的状态方程与输出方程为 1 12 2 1 () 4 () () () () 3 () () t t t et t t et λ λλ λ λ =− + + =− + & & 1 rt t () () = λ 试求(a)系统的微分方程表示。 (b)若输入et t () () = ε 时, 11 5 3 () () 32 6 t t rt e e t ε − − =+ − 求系统的起始状态λ(0 ) − 。 解(a)将 1 rt t () () = λ 代入 1 λ ( )t & 表示式,可得 2 ( ) 4 () () () dr t rt t et dt =− + + λ 由于题中给定系统有两个积分器,因而可用二阶微分方程表示,将上式两边求导,可得 2 2 2 () () 4 () () d r t d de t rt t dt dt dt =− + + λ & 将题中给定的 2 λ ( )t & 表示式代入后,可得 2 2 () () 4 () 3() () d r t d de t rt rt et dt dt dt + += + (b)求转移函数矩阵 1 H s C sI A B D () ( )− = − +

CAUCIEE将题中给定的状态方程与输出方程写成矩阵形式,得[a- a--0l-a于是(0-1-0(46 1-[ 式中 H - T[s=7 +4s+3[-3 s+4于是H0--0[ s+=+4$+3s+当e()=ε(t)时,系统的零状态响应为(0)=[H(S)E(5)]-[]-f(-e2)e(0)零输入响应为g()=r(0)-r:()[G+--]-(G-e)e0)按式"g(1)=Ce"(0-)
CIEE CAU 将题中给定的状态方程与输出方程写成矩阵形式,得 1 1 2 2 () () 41 1 ( ) ( ) 3 0 () 1 t t e t t t λ λ λ λ − = + − & & [ ] 1 2 ( ) ( ) 1,0 ( ) t r t t λ λ = 于是 [ ] 1 10 41 1 ( ) 1,0 01 30 1 Hs s − − = − − 式中 1 1 10 41 4 1 01 30 3 s s s − − − +− − = − 2 1 1 4 3 3 4 s s s s = + + − + 于是 [ ] 2 1 1 1 ( ) 1,0 4 3 3 41 s H s s s s = + + − + 2 1 1 43 3 s s s s + = = ++ + 当et t () () = ε 时,系统的零状态响应为 [ ] ( ) 1 1 3 () ( ) ( ) 1 3 1 (1 ) ( ) 3 zs t r t HsEs s s e t ξ ξ ε − − − = = + = − 零输入响应为 () () () zp zs r t rt r t = − = 11 5 1 3 3 (1 ) ( ) 32 6 3 tt t ee e t ε −− − + − −− 1 1 3 ( ) 2 2 t t eet ε − − = − 按式 ( ) (0 ) At zp r t Ce λ − =

CIEECAU于是[rg(0)l。=CIa(0)=0rg()。=CAa(0-)=1即[0 103]-4 17[2(0)]1,0][-3 [2(0-]得2(0-)=0[-42,(0°)+ 2 (0°)=1因此2(0-)=1, 2(0-)=1例8.8若离散系统的状态方程与输出方程为^(n+)] 「01[a(n)[o[3(+]-[- 5[(][]0)[y()]-[1 1 [2(m)][(n)][2-1][(n)初始状态为[(0]-[] x()=(m) [2(0-][2]试求系统的状态变量与输出变量。解题中给定4-[% 9]特征方程为[al-A=6 α-5)α?-5α+(α-2)(α- 3)== 0A的特征根为α,=2,α,=3,利用凯莱-哈密尔顿定理可得2"=C, +2C,3" =C,+3C,可解得C。=3·2"-2·3",C=3"-2",根据
CIEE CAU 于是 0 / 0 ( ) (0 ) 0 ( ) (0 ) 1 zp t zp t r t CI r t CA λ λ − = − = = = = = 即 [ ] [ ] 1 2 1 2 1 0 (0 ) 1,0 0 0 1 (0 ) 4 1 (0 ) 1,0 1 3 0 (0 ) λ λ λ λ − − − − = − = − 得 1 1 2 (0 ) 0 4 (0 ) (0 ) 1 λ λ λ − − − = − += 因此 1 2 λ λ (0 ) 1, (0 ) 1 − − = = 例 8.8 若离散系统的状态方程与输出方程为 1 1 2 2 ( 1) ( ) 01 0 ( ) ( 1) ( ) 1 6 5 n n x n n n λ λ λ λ + = + + − 1 1 2 2 () () 1 1 () () 2 1 yn n yn n λ λ = − 初始状态为 1 2 (0 ) 1 ,() () (0 ) 2 x n n λ ε λ − − = = 试求系统的状态变量与输出变量。 解 题中给定 0 1 6 5 A = − 特征方程为 2 1 5 6 6 5 I A α α αα α − −= = − + − = ( 2)( 3) 0 α − − == α A 的特征根为 1 2 α = = 2, 3 α ,利用凯莱-哈密尔顿定理可得 0 1 0 1 2 2 3 3 n n C C C C = + = + 可解得 0 1 32 23, 3 2 n n nn C C =⋅ −⋅ = − ,根据
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《信号与系统》课程教学资源(习题解答)第五章 拉普拉斯变换与系统分析.pdf
- 《信号与系统》课程教学资源(习题解答)第六章 变换与离散系统的z域分析.pdf
- 《信号与系统》课程教学资源(习题解答)第七章 连续时间系统的S域分析.pdf
- 《信号与系统》课程教学资源(习题解答)第四章 连续信号的傅利叶分析.pdf
- 《信号与系统》课程教学资源(习题解答)第三章 离散时间系统的时域分析.pdf
- 《信号与系统》课程教学资源(习题解答)第一章 信号与系统概述.pdf
- 《信号与系统》课程教学资源(习题解答)第二章 连续时间系统的时域分析.pdf
- 《信号与系统》课程授课教案(课件讲稿)第8章 系统状态变量分析.pdf
- 《信号与系统》课程教学课件(讲义)信号与系统实验指导书(共八个实验).pdf
- 《信号与系统》课程授课教案(课件讲稿)第6章 离散系统的Z域变换.pdf
- 《信号与系统》课程授课教案(课件讲稿)第5章 连续系统的S域分析.pdf
- 《信号与系统》课程授课教案(课件讲稿)第7章 系统函数.pdf
- 《信号与系统》课程授课教案(课件讲稿)第4章 连续系统的频域分析.pdf
- 《信号与系统》课程授课教案(课件讲稿)第2章 连续系统的时域分析.pdf
- 《信号与系统》课程授课教案(课件讲稿)第1章 信号与系统.pdf
- 《信号与系统》课程授课教案(课件讲稿)第3章 离散系统的时域分析.pdf
- 《信号与系统》课程教学大纲 Signals and Systems.pdf
- 《电路》课程教学资源(PPT课件)第18章 分布参数的电路.ppt
- 《电路》课程教学资源(PPT课件)第17章 非线性电路.ppt
- 《电路》课程教学资源(PPT课件)第16章 二端口网络.ppt
- 《数字电子技术》课程教学大纲(Digital Electronics).pdf
- 《数字电子技术》课程授课教案.doc
- 《机械测试技术基础》课程教学大纲 Mechanical Test Technology.pdf
- 《机械测试技术基础》课程教学资源(作业习题)机械工程测试技术基础习题集(无答案).doc
- 《机械测试技术基础》课程教学资源(作业习题)测试与检测技术基础习题集(清华大学,无答案).pdf
- 《机械测试技术基础》课程教学资源(作业习题)机械测试技术基础习题答案(第三版).pdf
- 《机械测试技术基础》课程教学资源(作业习题)机械工程测试技术基础五套试题(无答案).doc
- 《机械测试技术基础》课程教学资源(作业习题)机械工程测试技术基础试题(五套,无答案).doc
- 《机械测试技术基础》课程教学资源(作业习题)电子测试技术习题及答案.doc
- 《机械测试技术基础》课程教学资源(作业习题)测试技术习题与答案.doc
- 《机械测试技术基础》课程教学实验指导书(共六个实验).doc
- 《数字信号处理》课程教学大纲 Digital Signal Processing.pdf
- 《数字信号处理》课程教学课件(PPT讲稿)ch7-2 有限字长效应.ppt
- 《数字信号处理》课程教学课件(PPT讲稿)ch7-1 数字滤波器结构.ppt
- 《数字信号处理》课程教学课件(PPT讲稿)ch6 功率谱估计.ppt
- 《数字信号处理》课程教学课件(PPT讲稿)ch5_4 FIR优化设计.ppt
- 《数字信号处理》课程教学课件(PPT讲稿)ch5_3 频率取样法.ppt
- 《数字信号处理》课程教学课件(PPT讲稿)ch5_2 窗口法.ppt
- 《数字信号处理》课程教学课件(PPT讲稿)ch5_1 FIR性质.ppt
- 《数字信号处理》课程教学课件(PPT讲稿)ch4_4 双线性变换法.ppt
