《机械测试技术基础》课程教学资源（作业习题）电子测试技术习题及答案

电子测试技术习题 第一章习题 1填空题 1.信号可分为和 两太类。 2.确定性信号可分为 和 西类，前者的频谱特点是 。后者的谱特点是 3.信号的有效值又称为 一，有效值的平方称为一一，它描述测试信号的强度（信号的 平均功率) 4.绘制周期信号x(t)的单边频谱图，依据的数学表达式是 ，而双边频谱图的依据数学 表达式是 5.周期信号的傅氏三角级数中的·是从一到一展开的。傅氏复指数级数中的n是从 到■ 展开的。 6。周期信号x(t)的傅氏三角级数展开式中：an表示一，bn表示一，a表示 An表示一，Pn表示一n00表示一。 7.工程中常见的周期信号，其谐波分量幅值总是随谐波次数的增加而的，因此，没有必 要去那些高次的谐波分量。 &。则明方淡的侍氏损数：0=A头(oa+兮o30+.)周用三角该的传氏经数： π 马0-分兰。oso1+写os301+石o5+.它的直流分量分别是— 1 一。信号的收敛速度上，方波信号比三角波信号一。达到同样的测试精度要求时，方波信 号比三角波信号对测试装置的要求有更宽的」 9.。窗函数。(t)的频谱是t·sincrft,则延时后的窗函数o(t-)的频谱应是一 10.信号当时间尺度在压缩时，则其频带其幅值。例如将磁带记录仪即是例证。 11.单位脉冲函数6()的频谱为一，它在所有频段上都是一，这种信号又称一。 12.余弦函数只有—谱图，正弦函数只有—谱图。 13.因为m,x0d为有限值时，称x()为—信号。因此，瞬变信号属于_一，而周 期信号则属于 第1页共32页

电子测试技术习题 第 1 页 共 32 页 第一章习题 1 填空题 1. 信号可分为 和 两大类。 2. 确定性信号可分为 和 两类，前者的频谱特点是＿＿＿＿。后者的频谱特点是 ＿＿＿＿。 3. 信号的有效值又称为＿＿＿＿，有效值的平方称为＿＿＿＿，它描述测试信号的强度（信号的 平均功率） 4. 绘制周期信号 x（t）的单边频谱图，依据的数学表达式是＿＿＿＿，而双边频谱图的依据数学 表达式是＿＿＿＿。 5. 周期信号的傅氏三角级数中的 n 是从＿＿＿＿到＿＿＿＿展开的。傅氏复指数级数中的 n 是从 ＿＿＿＿到＿＿＿＿展开的。 6. 周期信号 x（t）的傅氏三角级数展开式中： n a 表示＿＿＿， n b 表示＿＿＿， 0 a 表示＿＿＿， A n 表示＿＿＿，  n 表示＿＿＿, 0 n 表示＿＿＿。 7. 工程中常见的周期信号，其谐波分量幅值总是随谐波次数 n 的增加而＿＿＿的，因此，没有必 要去那些高次的谐波分量。 8. 周期方波的傅氏级数： 1 0 0 2 1 ( ) (cos cos3 ) 3 A x t A t t    = + + + 周期三角波的傅氏级数： 2 0 0 2 4 1 1 ( ) (cos cos3 cos5 ) 2 9 25 A A x t t t    = + + + + ，它们的直流分量分别是＿＿＿和＿＿ ＿。信号的收敛速度上，方波信号比三角波信号＿＿＿。达到同样的测试精度要求时，方波信 号比三角波信号对测试装置的要求有更宽的＿＿＿。 9. 窗函数ω（t）的频谱是    sin c f ，则延时后的窗函数 ( ) 2 t   − 的频谱应是＿＿＿。 10. 信号当时间尺度在压缩时，则其频带＿＿＿其幅值＿＿＿。例如将磁带记录仪＿＿＿即是例证。 11. 单位脉冲函数  ( )t 的频谱为＿＿＿，它在所有频段上都是＿＿＿，这种信号又称＿＿＿。 12. 余弦函数只有＿＿＿谱图，正弦函数只有＿＿＿谱图。 13. 因为 2 lim ( ) T T T x t dt → − 为有限值时，称 xt( ) 为＿＿＿信号。因此，瞬变信号属于＿＿＿，而周 期信号则属于＿＿＿

电子测试技术习题 14计算积分值：∫6(t+5)e'cdh=一， 15.两个时间函数x)和x,(0的卷积定义式是一。 16.连续信号x(t)与单位脉冲函数1-1，)进行卷积其结果是：x)*61-6)=一。其几何 意义是： 17.单位脉冲函数61-)与在。点连续的模拟信号f0的下列积分： ∫f0)61-6)dh=一·这性质称为一 18已灯倚氏变换对1二6.根报颜移性质可狗e2:的特氏变换为一 19.已知傅氏变换对：x)三X(f)和x2()三X2()当x()=x()x)时 则X)=一。 20.非周期信号，时域为x(t),频域为X(),它们之间的傅氏变换与逆变换关系式分别是：X()= ，x(t)= 三、计算题 1.三角波脉冲信号如图1-1所示，其函数及频谱表达式为 A 图1-1 第2页共32页

电子测试技术习题 第 2 页 共 32 页 14. 计算积分值： ( 5) t  t e dt  −  +  = ＿＿＿。 15. 两个时间函数 1 2 x t x t ( ) ( ) 和 的卷积定义式是＿＿＿。 16. 连续信号 x（t）与单位脉冲函数 0  ( ) t t − 进行卷积其结果是： 0 x t t t ( ) ( )  − =  ＿＿＿。其几何 意义是：＿＿＿。 17. 单位脉冲函数 0  ( ) t t − 与 在 0 t 点连续的模拟信号 f t() 的下列积分： 0 f t t t dt ( ) ( )   −  − =  ＿＿＿。这一性质称为＿＿＿。 18. 已知傅氏变换对 1 ( )  f ，根据频移性质可知 0 j f t 2 e  的傅氏变换为＿＿＿。 19. 已知傅氏变换对： 1 1 2 2 1 2 x t X f x t X f x t x t x t ( ) ( ) ( ) ( ) ( ) ( ) ( ) 和 当 =  时， 则 X f ( ) =＿＿＿。 20. 非周期信号，时域为 x（t），频域为 X f ( ) ，它们之间的傅氏变换与逆变换关系式分别是： X f ( ) = ＿＿＿，x（t）= ＿＿＿。 三、计算题 1. 三角波脉冲信号如图 1-1 所示，其函数及频谱表达式为 /2 图 1-1 2 0 2 2 ( ) 0 A t t A x t t t t         ( + ) −       = − ( + )             当 当 当

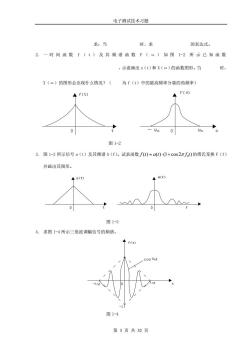
电子测试技术习题 求：当 时，求 的表达式。 2.一时间函数f(t)及其频谱函数下(“)如图1-2所示已知函数 ,示意画出x(t)和X()的函数图形。当 时 X(。)的图形会出现什么情况？（为f(t)中的最高频率分量的角频率） ◆f(t) 0n0 A 0 图1-2 3.图1-3所示信号a(t)及其频谱A(f)。试求函数f)=a()(1+cos2πf)的傅氏变换F(f) 并画出其图形 图1-3 4.求图1-4所示三角波调幅信号的频谱， 图1 第3页共32页

电子测试技术习题 第 3 页 共 32 页 2 ( ) sin ( ) 2 2 A f X f c    =  求：当 1 ( ) ( ) dx t x t dt = 时，求 1 1 x t X f ( ) ( ) 及 的表达式。 2. 一 时 间 函 数 f （ t ） 及 其 频 谱 函 数 F （ ω ） 如 图 1-2 所 示 已 知 函 数 0 0 ( ) ( ) cos ( ) m x t f t t =     设 ，示意画出 x（t）和 X（ω）的函数图形。当   0  m 时， X（ω）的图形会出现什么情况？（  m 为 f（t）中的最高频率分量的角频率） 图 1-2 3. 图 1-3 所示信号 a（t）及其频谱 A（f）。试求函数 0 f t a t f t ( ) ( ) (1 cos 2 ) =  +  的傅氏变换 F（f） 并画出其图形。 图 1-3 4. 求图 1-4 所示三角波调幅信号的频谱。 图 1-4

电子测试技术习题 参考答案 二、填空题 1,确定性信号：随机信号 2.周期信号：非周期信号：离散的：连续的 3.均方根值：均方值 4.傅氏三角级数中的各项系数(a,an,bn,An等)傅氏复指数级数中的各项系数(cn.c-nCal)。 6.a。一余弦分量的幅值：b。一正弦分量的幅值：4。一直流分量：A。一n次谐波分量的幅值：pn一n 次谐波分量的相位角：0，一n次谐波分量的角频率 7.衰诚 8.A:A/2:更慢：工作频带 .te.sincnfr 10.展宽：降低：慢录快放 1山，1：等强度：白噪声 12.实频：虚频 13.能量有限：能量有限：功率有限 14.e5 l5.∫x(0x,t-r)dr 16.x(t-1):把原函数图象平移至位置处 17.f(1o):脉冲采样 18.6f-f6) 19.Xf)*X) 20.X(f)=[X(f).e2"df 三、计算题 第4页共32页

电子测试技术习题 第 4 页 共 32 页 参考答案 二、填空题 1.确定性信号；随机信号 2.周期信号；非周期信号；离散的；连续的 3. 均方根值；均方值 4. 傅氏三角级数中的各项系数（ 0 , , , n n n a a b A 等 ）傅氏复指数级数中的各项系数（ , , n n n c c c − ）。 5.0；+∞；–∞；+∞ 6. n a —余弦分量的幅值； n b —正弦分量的幅值； 0 a —直流分量； A n - n 次谐波分量的幅值；  n -n 次谐波分量的相位角； 0 n -n 次谐波分量的角频率 7.衰减 8.A；A/2；更慢；工作频带 9. sin j f e c f      −   10.展宽；降低；慢录快放 11. 1；等强度；白噪声 12. 实频；虚频 13.能量有限；能量有限；功率有限 14. 5 e − 15. 1 2 x t x t d ( ) ( )    −  −  16. 0 x t t ( ) − ；把原函数图象平移至 位置处 17. 0 f t( ) ；脉冲采样 18. 0  ( ) f f − 19. 1 2 X f X f ( ) ( )  20. 2 ( ) ( ) j t X f X f e df   − =   三、计算题

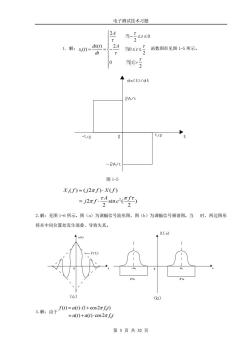
电子测试技术习题 [24当-5≤1≤0 1解：0=0 当0≤1≤号函数图形见图1-5所示。 /0 Adx(t)/dt 2A/1 t/a 0 1/2 -2A/1 图1-5 X()=(U2πf)X(f) 2sine() 2.解：见图16所示。图(a)为调幅信号波形图，图(b)为调幅信号频谱图。当时，两边图形 将在中间位置处发生混叠，导致失真。 (0) 3.解：由于f0=a0-+cos2 =a(t)+a()cos2πfd 第5页共32页

电子测试技术习题 第 5 页 共 32 页 1. 解： 1 2 0 2 ( ) 2 ( ) 0 2 0 2 A t dx t A x t t dt       −      = = −         当 当 当 t 函数图形见图 1-5 所示。 图 1-5 1 2 ( ) ( 2 ) ( ) 2 sin ( ) 2 2 X f j f X f A f j f c      =  =  2.解：见图 1-6 所示。图（a）为调幅信号波形图，图（b）为调幅信号频谱图。当 时，两边图形 将在中间位置处发生混叠，导致失真。 b b 3.解：由于 0 0 ( ) ( ) (1 cos 2 ) ( ) ( ) cos 2 f t a t f t a t a t f t   =  + = + 

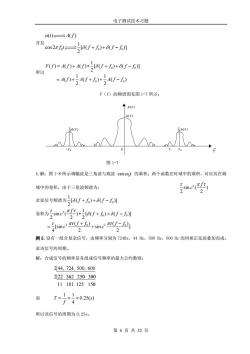
电子测试技术习题 a(t)A(f) 并 cos2ah=8U+)+8U-】 U)=A)+4)*6U+)+8f-6】 所以 =4+54U+60)+)4-0 F(f)的频谱图见图1-7所示： 图1-7 4.解：图1-8所示调幅波是三角波与载波c0s@,!的乘积。两个函数在时域中的乘积，对应其在频 域中的卷积，由于三角波频谱为： sine() 余弦信号频瑞为，6f+6)+6-6】 卷积为5c(要)6+6)+-6 in,sin 2 例5.设有一组合复杂信号，由频率分别为724细2,44z,500z,600z的同相正弦波叠加而成。 求该信号的周期。 解：合成信号的频率是各组成信号频率的最大公约数则： 244,724,500,600 222362250300 11181125150 而 1020 所以该信号的周期为0.25s。 第6页共32页

电子测试技术习题 第 6 页 共 32 页 并且 0 0 0 ( ) ( ) 1 cos 2 [ ( ) ( )] 2 a t A f    f t f f f f + + − 所以 0 0 0 0 1 ( ) ( ) ( ) [ ( ) ( )] 2 1 1 ( ) ( ) ( ) 2 2 F f A f A f f f f f A f A f f A f f = +  + + −   = + + + − F（f）的频谱图见图 1-7 所示： 图 1-7 4.解：图 1-8 所示调幅波是三角波与载波 0 cos t 的乘积。两个函数在时域中的乘积，对应其在频 域中的卷积，由于三角波频谱为： 2 sin ( ) 2 2 f c    余弦信号频谱为 0 0 1 [ ( ) ( )] 2   f f f f + + − 卷积为 2 0 0 1 sin ( ) [ ( ) ( )] 2 2 2 f c f f f f     + + −   2 2 0 0 ( ) ( ) [sin sin ] 4 2 2 f f f f c c    + − = + 例 5.设有一组合复杂信号，由频率分别为 724Hz，44 Hz，500 Hz，600 Hz 的同相正弦波叠加而成， 求该信号的周期。 解：合成信号的频率是各组成信号频率的最大公约数则： 2 44, 724, 500, 600 2 22        而 1 1 0.25( ) 4 T s f = = = 所以该信号的周期为 0.25s

电子测试技术习题 例6.利用6函数的抽样性质，求下列表示式的函数值： (1) f)=e3- 解：6函数是一类应用广泛的重要函数。在卷积运算、傅立叶变换及测试系统分析中，利用它可以 简化许多重要结论的导出。本例题的目的在于熟悉并正确应用6函数的性质。 (1)由于f0)8)=fo)6)fu)=e-60=e6u) 则f)=e-8)=e'60 例8.已知e(t)和ht)的波形图如下图(a),()所示，试计算e()与h(t)的卷积积分。 e0）*0）=e(r)ht-rdr +e(t) 4h(t) 112d 1 (0) (b) 解：(I)反折：将()与h()的自变量t用t替换。然后将函数hMx)以纵坐标为轴线进行反折 得到与hx)对称的函数。见图(c)所示。 (2)平移：将函数(1-t)沿t轴正方向平移时间t,得函数1-t)。(注意，这里的t是参变 量)，见图(d)所示。 (3)相乘并取积分：将(1一t)连续地沿t轴平移。对于不同的t的取值范围，确定积分上、下限， 并分段计算积分结果。 以下进行分段计算： a)当-<1一计，M!-)的他置知图回所示。追时0-)与没有重合部分.所型 e(t)*h)=0 ）一号1<1时，的位置如图①所示，这时-与《)的圈形重区为至 把它作为卷积积分的上、下限，得： 第7页共32页

电子测试技术习题 第 7 页 共 32 页 例 6．利用  函数的抽样性质，求下列表示式的函数值： （1） 3 1 ( ) ( ); t f t e t  − − = 解：  函数是一类应用广泛的重要函数。在卷积运算、傅立叶变换及测试系统分析中，利用它可以 简化许多重要结论的导出。本例题的目的在于熟悉并正确应用  函数的性质。 （1）由于 f t t f t ( ) ( ) ) = () • (   3 1 1 ( ) ( ) ( ) t f t e t e t   − − − = = 则 3 1 1 ( ) ( ) ( ) t f t e t e t   − − − = = 例 8.已知 et() 和 ht() 的波形图如下图(a),(b)所示，试计算 et() 与 ht() 的卷积积分。 e t h t e h t d ( ) ( ) ( ) ( )     −  = −  解：（1）反折：将 et() 与 ht() 的自变量 t 用τ替换。然后将函数 h( )  以纵坐标为轴线进行反折， 得到与 h( )  对称的函数 。见图(c)所示。 （2）平移：将函数 h t( ) − 沿τ轴正方向平移时间 t，得函数 h t( ) − 。（注意，这里的 t 是参变 量），见图(d)所示。 （3）相乘并取积分：将 h t( ) − 连续地沿τ轴平移。对于不同的 t 的取值范围，确定积分上、下限， 并分段计算积分结果。 以下进行分段计算： （a）当 1 2 −   − t 时， h t( ) − 的位置如图(e)所示。这时 h t( ) − 与没有重合部分。所以 e t h t ( ) ( ) 0  = （b） 1 1 2 −  t 时，的位置如图(f)所示。这时 h t( ) − 与 e( )  的图形重叠区间为 1 2 − 至 t。 把它作为卷积积分的上、下限，得：

电子测试技术习题 40m0=0-0r-+6 (©)11，并且1-2-同时1-23 卷积结果见图()所示。 hct-t 第8页共32页

电子测试技术习题 第 8 页 共 32 页 2 1 2 1 1 ( ) ( ) 1 ( ) 2 4 4 16 t t t e t h t t d   −  =  − = + +  （c） 3 1 2  t 时（即 t 1 ，并且 1 2 2 t −  − 时），则的位置如图(g)所示，这时的图形重叠区 间为（ 1 2 − ，1），把它作为卷积积分的上、下限，得： 1 2 1 3 3 ( ) ( ) 1 ( ) 2 4 16 t e t h t t d t   −  =  − = −  （d） 3 3 2  t 时，（即 1 2 2 t −  − ，同时 t − 2 1 ），由图(h)可知积分区间为（t-2，1）。得 2 1 2 1 3 ( ) ( ) 1 ( ) t 2 4 2 4 t t e t h t t d   −  =  − = − + +  （e） 3   t 时， h t( ) − 与 e( )  无重叠部分，见图(i)所示，这时 e t h t ( ) ( ) 0  = 归纳以上结果得 2 2 1 0 2 1 1 1 4 4 16 2 3 3 3 ( ) ( ) 1 4 16 2 3 3 4 2 4 2 0 t t t t t e t h t t t t t t  −    −    + + −       = −      − + +          当 当 当 当 当 卷积结果见图（j）所示

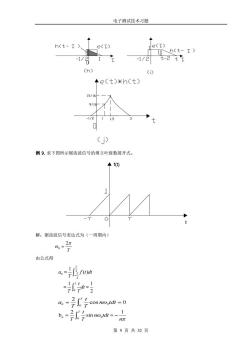
电子测试技术习题 h(t-t ) e(t) e() (t-t> -1/2 (h) +e(t)米h(t) 15/16 9/16 15 0 (j) 例9.求下图所示锯齿波信号的傅立叶级数展开式。 ◆f⑩ 解：锯齿波信号表达式为（一周期内） -27 由公式得 a=值oa a-子g7 o=0 。号mm= 第9页共32页

电子测试技术习题 第 9 页 共 32 页 例 9.求下图所示锯齿波信号的傅立叶级数展开式。 t f(t) 解：锯齿波信号表达式为（一周期内） 0 2 T   = 由公式得 2 0 2 0 1 ( ) 1 1 2 T T T a f t dt T t dt T T − = = =   0 0 2 cos 0 T n t a n tdt T T = =   0 0 2 1 b sin T n t n tdt T T n   = = − 

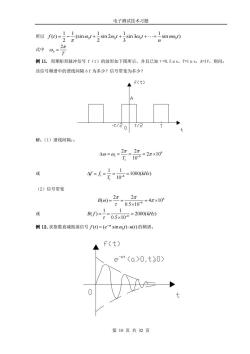
电子测试技术习题 所以0-号2ema时+号n2ay+写n3o+.+坊 inno) 例11.周期矩形脉冲信号f(t)的波形如下图所示，并且己知t=0.5μ5，T=1μs,A1V,则问 该信号缬谱中的谱线间隔△f为多少？信号带宽为多少？ A f(t) t/col t/i 解：(1)谱线间隔： =-7-2ax0 或 y=人-7d=lw0u 1 (2)信号带宽 2π 或 8-o5i0=20na） 例12.求指数衰减振荡信号f=(esin,)u)的频谱。 A f(t) et (a>o,t>0) 第10页共32页

电子测试技术习题 第 10 页 共 32 页 所以 0 0 0 0 1 1 1 1 1 ( ) (sin sin 2 sin 3 sin ) 2 2 3 f t t t t n t n      = − + + + + 式中 0 2 T   = 例 11. 周期矩形脉冲信号 f（t）的波形如下图所示，并且已知τ=0.5μs，T=1μs，A=1V，则问； 该信号频谱中的谱线间隔Δf 为多少？信号带宽为多少？ 解：（1）谱线间隔：： 6 1 6 1 2 2 2 10 T 10      −  = = = =  或 1 6 1 1 1 1000( ) 10 f f kHz T −  = = = = （2）信号带宽 6 6 2 2 ( ) 4 10 0.5 10 B      − = = =   或 6 1 1 ( ) 2000( ) 0.5 10 B f kHz  − = = =  例 12.求指数衰减振荡信号 0 ( ) ( sin ) ( ) at f t e t u t  − =  的频谱