《数字信号处理》课程教学课件（PPT讲稿）ch4_1 模拟滤波器设计

IIR数字滤波器的设计模拟低通滤波器设计模拟域频率变换·脉冲响应不变法双线性变换法内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 •模拟低通滤波器设计 •模拟域频率变换 •脉冲响应不变法 •双线性变换法 IIR数字滤波器的设计

IIR滤波器设计的基本思想1)将数字滤波器的设计为模拟滤波器的设计。2)设计满足技术指标的模拟滤波器。3）将模拟滤波器转换为数字滤波器内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 1)将数字滤波器的设计为模拟滤波器的设计。 2)设计满足技术指标的模拟滤波器。 3)将模拟滤波器转换为数字滤波器。 IIR滤波器设计的基本思想

模拟低通滤波器的设计模拟滤波器的技术要求Butterworth模拟低通滤波器·切比雪夫I型模拟低通滤波器切比雪夫IⅡ型模拟低通滤波器椭圆低通滤波器内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 模拟低通滤波器的设计 •模拟滤波器的技术要求 •Butterworth模拟低通滤波器 •切比雪夫II型模拟低通滤波器 •切比雪夫II型模拟低通滤波器 •椭圆低通滤波器

模拟滤波器的技术要求H(j)|通带截止频率0p1-8D阻带截止频率0,:>过渡带Sp通带波动通带一Ss:阻带一>阻带波动s00",0A, = -20log1o(1-S,)通带衰减（db）（passbandAttenuation）A, = -20log1o 8,阻带衰减（db）(stopbandAttenuation）滤波器的Gain函数G(@)=20log1o/H(ja)ldB内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 模拟滤波器的技术要求 w p : 通带截止频率 ws: 阻带截止频率 d p: 通带波动 d s : 阻带波动 20log (1 ) Ap = − 10 −d p 通带衰减(db)(passband Attenuation) As 10 d s = −20log 阻带衰减(db )(stopband Attenuation) |H( jw)| 1 0 通带 过渡带 阻带 p w s w s d p 1−d w G(w)=20log10|H(jw)| dB 滤波器的Gain函数

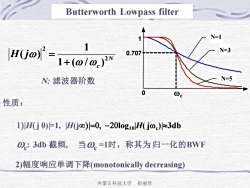
Butterworth Lowpass filterN=11N=3H(jw)0.7071+( / 0.)2NN=5N:滤波器阶数0Oc性质：1)H(j 0)-1,H(j)/=0, -20log1o|H(j@)/~3dbの：3db截频，当の.=1时，称其为归一化的BWF2）幅度响应单调下降（monotonicallydecreasing）内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 wc 1 0 N=1 N=3 N=5 0.707 Butterworth Lowpass filter N c H j 2 2 1 ( / ) 1 ( ) w w w + = N: 滤波器阶数 性质： 2)幅度响应单调下降(monotonically decreasing) 1)|H( j 0)|=1, |H(j)|= −2log10|H( jwc )|3db wc : 3db 截频, 当wc =1时，称其为归一化的BWF

3）H(jの)/2在-0点1到2N-1阶导数零。称为最大平坦性(maximallyflatmagnitudefilter)在の=0点做Taylorseries展开[H(jo)° =1-(-)2N +(~)4N 0.0归一化的Butterworth滤波器(BWF1[Hro(jo) =1 +02N任意的BWF和归一化BWF的关系H(s) = HLo(s / @c)内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 在w=点做Taylor series展开 = − + N − c N c H 2 4 2 (j ) 1 ( ) ( ) w w w w w L N H j 2 2 0 1 1 ( ) w w + = 归一化的Butterworth滤波器(BWF) 任意的BWF和归一化BWF的关系 ( ) ( / ) L0 c H s = H s w 3) |H(jw)|2在w=点1到2N−1阶导数零。称为最大平坦性。 (maximally flat magnitude filter)

归一化Butterworth滤波器的极点条件：h(t)是实的 H(jの)=H*(-jの)H(s)H(-s)| s=jo = H(jo)H(-jo)=|H(jo)i1H(s)H(-s)=1 +(-js)2NSk =(-1)1/2N j = (e-jn+2 k μ1/2 N 极点： 2k-1j元(-2N2; k = 1,2...,2N=e共有2N个极点，为了保证系统的稳定，选左半平面的N个极点。内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 归一化Butterworth滤波器的极点 2 j ( ) ( ) (jw) ( jw) (jw) H s H −s s= w = H H − = H 条件：h(t)是实的 H( jw ) =H*(− jw ) N s H s H s 2 1 ( j ) 1 ( ) ( ) + − − = 极点： ( 1) j {e } j 1/ 2N jπ 2 πk 1/ 2N k s − + = − = N k N k e ; 1,2 ,2 ) 2 2 1 2 1 jπ ( = =  − + 共有2N个极点，为了保证系统的稳定，选左 半平面的N个极点

2 k-11+j元 (22N;k = 1,2...,N为左半平面的N个极点Sk =e-2 k+1 2(N+1-k)-1j元(1-2)j元(-2 2 N22 N=e=eS n+1-k2k-1I- j元 (2 2N= Sk=e(s-$ )(s-st)=s? -2Re(s, )s+(sl(2k -1)元= s2 +2sin(s+l2N内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 s N k N k k e ; 1,2 , ) 2 2 1 2 1 jπ ( = =  − + 为左半平面的N个极点 2 ) 2 2 ( 1 ) 1 2 1 jπ ( 1 e − + − − + + − = N N k N k s 2 2 ( )( ) 2Re( ) k k k k s − s s − s = s − s s + s  ) 1 2 (2 1) 2sin( 2 + − = + s N k s  ) 2 2 1 2 1 jπ ( e N − k+ − + = ) 2 2 1 2 1 jπ ( e N k− − + = k = s

·当N为偶数时N12H(s)=IIs? + 2(sin 0,)s +1k=1 0k =(2k -1)元/(2N)例: N=2,=元/4 ; k=10k =(2k -1)元/(2N)1H(s)= -$? +/2s+10 =(2k -1)元/8 =元 /8, 3 元 /8; k-1 ,2例: N=4,1H(s)= -(s2 +2sin(元/8)s+1)(s2 +2sin(3元/8)s+1)1(s2 + 0.7654 s +1)(s2 +1.8478 s +1)内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 •当N为偶数时 2(sin ) 1 1 ( ) 2 / 2 1 + + = = s s H s k N k  (2k 1)π /(2N)  k = − 例：N=2, (2k 1)π /(2N)  k = − =/4 ; k=1 2 1 1 ( ) 2 + + = s s H s 例：N=4,  k = (2k −1)π /8 = / 8 3  / 8; k=1 ,2 ( 2sin( π /8) 1)( 2sin(3π /8) 1) 1 ( ) 2 2 + + + + = s s s s H s ( 0.7654 1)( 1.8478 1) 1 2 2 + + + + = s s s s

·当N为奇数时2(N+1)/2-11j元(+22N=ej =-1S(N+1)/2 =e(N-1)/2111IH(s) = s2 +2(sin0,)s+1(s + 1) k=10, =(2k -1)元/(2N)1H(s)=例: N=1(s + 1), =(2 -1)元 /(2 ×3)=元/6N=31H(s)=(s+1)(s°+s+1)内蒙古科技大学崔丽珍

内蒙古科技大学 崔丽珍 •当N为奇数时 ) 2 2( 1)/ 2 1 2 1 jπ ( ( 1)/ 2 e N N N s + − + + = 2(sin ) 1 1 ( 1) 1 ( ) 2 ( 1)/ 2 + 1 + + =  − s = s s H s k N k  (2k 1)π /(2N)  k = − 例：N=1 ( 1) 1 ( ) + = s H s N=3 (2 1)π /(2 3) 1 = −  = π / 6 ( 1)( 1) 1 ( ) 2 + + + = s s s H s e 1 jπ = = −