《数字信号处理》课程教学课件（PPT讲稿）ch5_1 FIR性质

FIR数字滤波器的设计线性相位FIR滤波器的性质·窗函数法设计FIR滤波器频率取样法设计线性相位FIR滤波器·线性相位FIR滤波器的优化设计

FIR数字滤波器的设计 •线性相位FIR滤波器的性质 •窗函数法设计FIR滤波器 •频率取样法设计线性相位FIR滤波器 •线性相位FIR滤波器的优化设计

线性相位FIR滤波器的性质线性相位系统的时域特性·线性相位系统的频域特性·线性相位系统H(z)的零点分布特性

线性相位FIR滤波器的性质 •线性相位系统的时域特性 •线性相位系统的频域特性 •线性相位系统H(z)的零点分布特性

FIR滤波器的定义M-kH(z)=Z bkzk=0M阶(长度N=M+1)的FIR数字滤波器16k =0,1,..., Mh[k] =0其它

FIR滤波器的定义 k k M k H z b z − = =  0 ( ) M阶(长度N=M+1) 的FIR数字滤波器    = 0 其它 bk k 0,1,,M h[k ] =

FIR滤波器的特点1)hlkl在有限范围内非零，系统总是稳定的2)容易设计成线性相位3）可利用FFT实现4）运算量比IR大

FIR滤波器的特点 1)h[k]在有限范围内非零，系统总是稳定的。 2)容易设计成线性相位 3)可利用FFT实现 4)运算量比IIR大

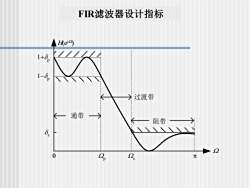
FIR滤波器设计指标Heig)1+8p1-81W过渡带XO一通带→?阻带SS----20&p2,元

通带 过渡带 阻带   p  s ej   p − p s FIR滤波器设计指标

严格线性相位定义H(ej9)=H(ejg)lej(2)若蚁2)=一 α2,则称系统H(z)是严格线性相位的。例：单频信号exp(j2k)通过线性相位(LTI)系统的响应T(ejk ) =|H(ej. )lej. (k-a)

严格线性相位定义 j j j ( ) (e ) (e ) e     H = H 例： 单频信号exp(j0 k)通过线性相位(LTI)系统的响应 j j j ( ) 0 0 0 {e } (e ) e    − = k k T H 若()= − , 则称系统H(z)是严格线性相位的

广义线性相位定义H(ej)= A(2)e-i(2+B)A(2)称为幅度频函数

广义线性相位定义 j j( ) (e ) ( )e     −  H = A A()称为幅度频函数

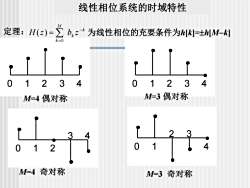
线性相位系统的时域特性M定理：H(z)= bkz-k 为线性相位的充要条件为h[K]=±h[M-k]k=011V02340￥1￥1234-M=3 偶对称M=4 偶对称2334014012M=4奇对称M=3 奇对称

线性相位系统的时域特性 0 1 2 3 4 M=4 偶对称 0 1 2 3 4 M=3 偶对称 0 1 2 3 4 M=4 奇对称 0 1 2 3 4 M=3 奇对称 定理： 为线性相位的充要条件为h[k]=h[M−k] k k M k H z b z − = =  0 ( )

线性相位系统的频域特性1) 1型：(h[k]=h[M-k],M为偶数)例: M=4 , h[k]={h[0], h[1], h[2], h[1], h[0]]H(ej2)= h[0](1+e-j42)+h[1](e-je +e-j32)+h[2]e-j2= 2h[0]e-j2 cos22+ 2h[1]e-j22 cos 2+h[2]e- 22A(Q) = h[2]+ 2h[2 -1]cos .Q + 2h[2 - 2]cos2 2L=M/2VL2h[L-k]cos kQ=A(②) = h[L]+Za[k]coskQk=1k=0

线性相位系统的频域特性 1) 1型: (h[k]=h[M−k], M为偶数) 例：M=4 , h[k]={h[0], h[1], h[2], h[1], h[0]}  4  3 2 ( ) [0](1 ) [1]( ) [2] j j j j j H e h e h e e h e − − − − =          2 2 2 2 [0] cos2 2 [1] cos [2] j j j h e h e h e − − − =   A() = h[2] 2h[2 −1]cos  2h[2 − 2]cos2 A  h L h L k k a k k L k L k ( ) [ ] 2 [ ]cos [ ]cos 1 0   = = =  − = L = M / 2

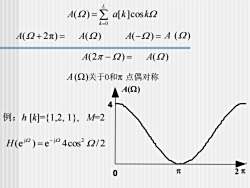
BA(2)=Za[k]cos k?k=0A(Q+2元)=A(2)A(-2)= A (2)A(2元- ②)=A(2)A(Q)关于0和元点偶对称A(2)4例：h [k]={1,2, 1}, M-2H(ej2)=e-j 4cos? Q/22元元0

A  a k k L k ( ) [ ]cos 0 = = A(  2π) = A( ) A(−) = A () A()关于0和 点偶对称 例：h [k]={1,2, 1}, M=2 (e ) e 4cos / 2 j j 2   −  H =  2  4 0 A() A(2 −) = A( )