《机械测试技术基础》课程教学资源（作业习题）测试技术习题与答案

机械测试技术基出 习 题 解 答 授课教师：杨文志

机械测试技术基础 习 题 解 答 授课教师：杨文志

第一章习题(P29) 1-1以下信号，个是周期信号？哪个是准周期信号？哪个是既变信号？它们的领谱各其传哪些符征？ (1)cos 2fte (2）sin2xfot+4 sin fot (3)o92xfk+2cos3πf.t 解： (1)瞬变信号一指数衰减振荡信号，其频谱具有连续性和衰减性。 (2)准周期信号，因为各简谐成分的频率比为无理数，其频谱仍具有离散 性。 (3)周期信号，因为各简谐成分的频率比为无理数，其频谱具有离散性、 谐波性和收敛性。 1-2求信号，6e=如2：的有效值（均方根值z-√2(0）： 解：x(t)=sin2:的有效值（均方根值）： VT。 = j0-cs40 1 1 2To dt= (T。一4河 smn4对。) 2T。 4 1 V2T。 sn4河oT。）=1/V2 1-}用傅里叶级数的三角茵数展开式和复指数展开式，求周期三角波（图121）的频谱，并作频谱州 1

1 第一章 习 题（P29） 解： （1）瞬变信号－指数衰减振荡信号，其频谱具有连续性和衰减性。 （2）准周期信号，因为各简谐成分的频率比为无理数，其频谱仍具有离散 性。 （3）周期信号，因为各简谐成分的频率比为无理数，其频谱具有离散性、 谐波性和收敛性。 解：x(t)=sin2 f t  0 的有效值（均方根值）： sin 4 ) 1/ 2 4 1 ( 2 1 sin 4 ) 4 1 ( 2 1 (1 cos 4 ) 2 1 sin 2 1 ( ) 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 2 0 0 0 0 0 = − = = − = − = =    f T f T T f t f T T f t dt T f t dt T x t dt T x T T T T rms      

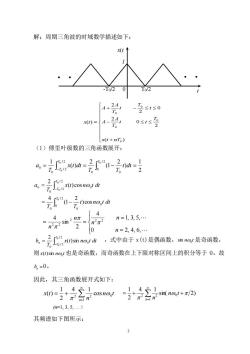
解：周期三角波的时域数学描述如下： x(1 0/20 4+-1≤0 0=4-24, x(t+nT) (1)傅里叶级数的三角函数展开： 2 .(csme T。 「4 京m- 4 n=l,3,5,. = 20 n=2,4,6, 么=号0由@山，式中由于0是偶函数，血@是奇函数。 则x)snn,1也是奇函数，而奇函数在上下限对称区间上的积分等于0。故 b。=0。 因此，其三角函数展开式如下： 1+41 1,41 0=2+产Σosna/2+7Σ7mau+/2 ml,3,5,.) 其频谱如下图所示：

2 解：周期三角波的时域数学描述如下： （1）傅里叶级数的三角函数展开： ，式中由于 x(t)是偶函数， n t 0 sin  是奇函数， 则 x t n t 0 ( )sin  也是奇函数，而奇函数在上下限对称区间上的积分等于 0。故 bn = 0。 因此，其三角函数展开式如下： 其频谱如下图所示： -T0/2 0 T0/2 1 x(t ) t . . . . . .          + −   + −   = ( ) 2 0 2 0 2 2 ( ) 0 0 0 0 0 x t nT T t t T A A t T t T A A x t 2 1 ) 2 (1 2 ( ) 1 / 2 0 0 0 / 2 / 2 0 0 0 0 0 = = − = −  T T T t dt T T x t dt T a   = − = − / 2 0 0 0 0 / 2 / 2 0 0 0 0 0 ) cos 2 (1 4 ( ) cos 2 T T T n t n t dt T T x t n t dt T a        = = = =   0 2, 4, 6, 1, 3, 5, 4 2 sin 4 2 2 2 2 2 n n n n n    − = / 2 / 2 0 0 0 0 ( )sin 2 T T n x t n t dt T b    = = + 1 2 2 0 cos 4 1 2 1 ( ) n n t n x t     = = + + 1 2 2 0 sin( 2) 4 1 2 1 n n t n    (n=1, 3, 5, .）

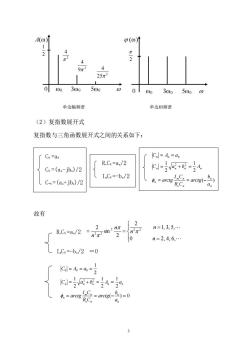
4) p(@) 4 25π 000 300 000 0100300500 单边幅须谱 单边相频谱 (2)复指数展开式 复指数与三角函数展开式之间的关系如下： Co=ao Col=Ao =ao R.Cx=a/2 Cw=(a.-jb.)/2 G园+6-4 I.Cw=-b./2 C-x=(a.+jb.)/2 arct B.C 故有 2 2 =n2π n=13,5,. n=2,4,6,. LI.Cw=-b./2=0 Cd=4=4=2 1 c=)匠+成=4=0 a 3

3 （2）复指数展开式 复指数与三角函数展开式之间的关系如下： 故有 ( ) 0 2 1 = 2 1 2 1 2 1 n 2 2 0 0 0 = = − = = + = = = = n n e n m n n n n n n a b arctg R C I C arctg C a b A a C A a  0  A() 0 30 50 0 0 30 50   () 2 4  2 9 4  2 25 4  2 1 2  C0 =a0 CN =(an-jbn)/2 C-N =(an+jbn)/2 ReCN =an/2 ImCN =-bn/2 ( ) 2 1 2 1 2 2 0 0 0 n n e n m n n n n n n a b arctg R C I C arctg C a b A C A a = = − = + = = =  ReCN =an/2      = = = =   0 2, 4, 6, 1, 3, 5, 2 2 sin 2 2 2 2 2 2 n n n n n    ImCN =-bn/2 ＝0 单边幅频谱 单边相频谱

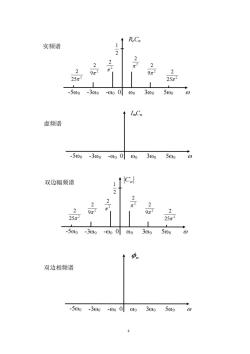
R.Cn 实频谱 2 2 2 2品 2 25r2 -500 -300-00000 300 InCn 虚频谱 -500-300-000003005000 双边幅频谱 2 2 2 2 2 9 25 25m -500-300-000003005000 中n 双边相频谱 -500-300-000003005000

4 0  n -50 -30 -0 0 30 50 0 0 30  2 2  2 1 2 9 2  2 25 2  -30 -0 50 2 9 2  2 25 2  -50 2 2  Cn 0  ImCn -50 -30 -0 0 30 50 0  ReCn 0 30 2 2  2 1 2 9 2  2 25 2  -30 -0 50 2 9 2  2 25 2  -50 2 2  虚频谱 双边相频谱 实频谱 双边幅频谱

1-4求三角形窗函数（图1.22）的频谱，并作频谱图。 解：该三角形窗函数是一非周期函数，其时域数学描述如下： x(t) 1+2, ≤150 x(0)= 2 0≤1≤ -To/2 0 To/2 用傅里叶变换求频谱。 x(xed-Jr see d =0-20e*a+0+2h T a-200+20km T -7g-20eg。na-2 To ++2)ea-nema+2m 1 7p品r啡-el e-1-1tom l-cos 1 1 π2f2T ·2sm2 2 2-五snc2 2(y2 2 2

5 解：该三角形窗函数是一非周期函数，其时域数学描述如下： 用傅里叶变换求频谱。 -T0/2 0 T0/2 1 x(t) t        −   + −   = 2 0 2 1 0 2 2 1 ( ) 0 0 0 0 T t t T t T t T x t  − − −  − = = / 2 / 2 2 2 0 0 ( ) ( ) ( ) T T j f t j f t X f x t e dt x t e dt   2 sin 2 ) 2 ( 2 sin 2 2 2sin 1 [1 cos ] 1 [ 1 1 ] 2 1 [ ] 2 1 2 2 ]} 2 ] [1 2 {[ 1 2 1 )]} 2 ) (1 2 [(1 )] 2 ) (1 2 {[(1 2 1 ) ] 2 ) (1 2 [ (1 2 1 ) 2 ) (1 2 (1 0 2 0 0 2 2 0 0 2 0 0 0 2 2 0 2 2 0 2 2 0 / 2 / 2 2 0 2 0 0 / 2 2 0 / 2 0 2 0 0 / 2 0 0 2 / 2 2 0 / 2 0 0 / 2 2 0 2 0 0 / 2 2 0 / 2 0 2 0 0 / 2 2 0 / 2 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 f T c T f T f T T f T f T f T f T e e f T e e j f T j f e dt T e dt j f T t T t e e d T t T t e e d j f T t de T t de j f T t e dt T t e dt T j f T j f T T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t                            =  =  = − =  = − − − + − −  − = − + + − − = + + − + − − − − = − + + − = = − + + − − − − − − − − − − − − − − − − − − −        

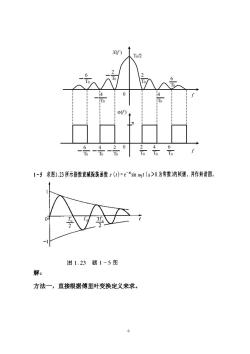
To/2 0 (f) 20 一一而一 而而而 f 1-5求图1.23所示指数衰减振荡函数r(t)=e“s如如t(a>0为常数)的频谱，并作频谱图。 37 2 出1.23题1-5图 解： 方法一，直接根据傅里叶变换定义来求。 6

6 解： 方法一，直接根据傅里叶变换定义来求。 X(f ) T0/2 0 2 T0 2 T0 f 6 T0 6 T0 (f )  0 2 T0 4 T0 6 T0 2 T0 4 T0 6 T0 4 T0 4 T0 f

X(o)="x(t)e-dt e"sin wot edt =。mrew-eh -ey-eyd e-(atjo-j)t a+-)61 =[1 2'a+j(o+@o)a+j(o-@) 00 =a2+a2-02+2a0 方法二，根据傅里叶变换的频移特性来求。 单边指数衰减函数： 0t0,t≥0 其傅里叶变换为 F(@)=["f(t)e-dt =e-a.e-iedt =eae-a oo -(a+jo)0 1 (a+jo) a-jo =+0

7 方法二，根据傅里叶变换的频移特性来求。 单边指数衰减函数： 其傅里叶变换为       = − 0, 0 0 0 ( ) e a t t f t at 2 2 0 ( ) 1 ( ) 0 ( ) ( )         + − = + =  − +  = =  = − − − −  −  −   a a j a j a j e e e e dt F f t e dt at j t at j t j t                            a j a a j a j j a j j e a j j j e e e dt j e e dt j e e t e dt X x t e dt a j j t a j j t a j j t a j j t a j t j t j t a t j t j t 2 ] ( ) 1 ( ) 1 [ 2 ] ( ) ( ) [ 2 [ ) 2 ( ) 2 sin ( ) ( ) 2 2 0 2 0 0 0 0 0 ( ) 0 0 ( ) ( ) ( ) 0 ( ) 0 0 0 0 0 0 0 0 0 + − + = + − − + + = + − + − + + = = − =  − =  =  − + −  − + + − + + − + −  − + −  − −  −  −    

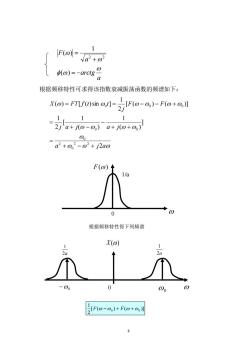
1 F(o)= va'+o Ke)-adg 根据频移特性可求得该指数衰减振荡函数的频谱如下： X(@)=FTIf(t)sin @ot]= Ra-a)-Fo+a】 1 1 1 2a+jo-,)a+j@+) 00 =a2+w2-02+j2a F(o)↑ 1/a 0 根据频移特性得下列频谱 X( Fo-eJ+Fro+a】

8 a arctg a F      = − + = ( ) 1 ( ) 2 2 根据频移特性可求得该指数衰减振荡函数的频谱如下： 0  0 −0 F() 0 X () 1/a 2a 1 2a 1 根据频移特性得下列频谱               a j a j a j a j F F j X FT f t t 2 ] ( ) 1 ( ) 1 [ 2 1 [ ( ) ( )] 2 1 ( ) [ ( )sin ] 2 2 0 2 0 0 0 0 0 0 + − + = + + − + − = = = − − +  [ ( ) ( )] 2 1 F  −0 + F  +0

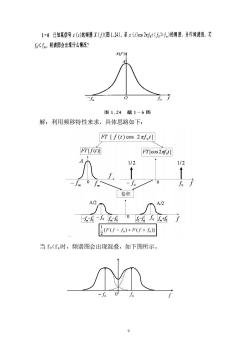
1-6已知某信号z(c)的颜谱X(U图L.24),求xt)s2xft(乐6》5，)的领谱.并作领谱。若 6<。,颊请图会出现什么情况？ 图1.24题1-6图 解：利用频移特性来求，具体思路如下： FT[f(t)cos2πfo1] FTUSO] FT[cos2对] 1/2 1/2 「卷积 A/2 Ff-f+F+列 当f<f.时，频谱图会出现混叠，如下图所示

9 解：利用频移特性来求，具体思路如下： 当 f0<fm时，频谱图会出现混叠，如下图所示。 0 f 0 − f 0 f A/2 A/2