《信号与系统》课程教学资源（习题解答）第六章 变换与离散系统的z域分析

CIEECAU第六章z变换与离散系统的z域分析本章重点1.求序列的=变换并确定收敛区间。1）利用=变换的定义式；(2)采用幂级数展开法；用=变换的性质。(3)2.=反变换的确定（1）幂级数展开法（长除法）：121部分分式展开法；(3)围线积分法（留数法）3.由拉氏变换X(s)求:变换X(a)4.利用≥变换求解差分方程。5.利用=变换分析系统，系统函数H()及零、极点图，系统的单位样值响应及频率响6.离散系统得模型。例6.1求下列序列x(n)=(n-3)e(n)的≥变换，并标明收敛域解x(n)=(n-3)e(n)= ne(n) -3e(n)因为[e(m]->1[ne(m)=(-1'=>1所以X(a)= 5[x(n)]=3>1(=-1)24z-32>1"(-I若用时移（位移）性质x(n) X(2)[x()+ 2 ()--x(n-m)e(n)α2x(n-m)e(n-m)"X(2)

CIEE CAU 第六章 z 变换与离散系统的 z 域分析 本章重点 1.求序列的 z 变换并确定收敛区间。 （1） 利用 z 变换的定义式； （2） 采用幂级数展开法； （3） 用 z 变换的性质。 2. z 反变换的确定. （1） 幂级数展开法（长除法）； （2） 部分分式展开法； （3） 围线积分法（留数法）。 3.由拉氏变换 X ( )s 求 z 变换 X ( )z 。 4.利用 z 变换求解差分方程。 5.利用 z 变换分析系统，系统函数 H z( ) 及零、极点图，系统的单位样值响应及频率响 应。 6.离散系统得模型。 例 6.1 求下列序列 x() 3 () nn n = − ( )ε 的 z 变换，并标明收敛域 解 x() 3 () () 3() n n n nn n =− = − ( )ε ε ε 因为 [ ] () , 1 z n z ξ ε = − z >1 [ ] ( )2 () , 1 z n n z ξ ε = − z >1 所以 [ ] ( )2 () () 3 , 1 1 1 z z X z xn z z z = = −⋅ > ξ − − ( ) 2 2 4 3 1 z z z − = − z >1 若用时移（位移）性质 x( ) n ↔ X ( )z 1 ( )() () () m k k m x n m n z X z xk z ε − − − =−   −↔ +     ∑ ( )( ) () m x n m n m z Xz ε − − −↔

CIEECAU则由ne()((n-3)e(m)台2[()+(-3)2 +(-2): +(-1)]_ 4z-32[=>1(--1)或由(n-3)e(n)=(n-3)e(n-3)-38(n)-28(n-1)-8(n-2) -2--1--(z-1)24z-32>1(=-1)?例6.2求下列信号的单边≥变换，并标明相应的收敛域。(a) x(n)=8(n+4)+8(n-4)+8(n)+3"e(-n)()(b)x(n)e(n+3)（)解，这种题解答过程并不复杂，只是要求审题细心，正确理解单边变换的概念，明确n的取值范围是n≥0。(a）由定义式≤[x(m)] -2 (n)-"-2[6(+4)+(n-4)+(m)+*e(-m)"2+1+1=2+2, 1>0(b)5[)-=2() 0+3)-*-2() c0)--例6.3求下列序列的变换，并指出收敛域

CIEE CAU 则由 ( )2 ( ) 1 z n n z ε ↔ − ( ) ( ) ( ) ( ) 3 32 n n z Xz z z z 3 () () 3 2 1 ε − − ↔ +− +− +−     ( ) 2 2 4 3 1 z z z − = − ， z >1 或由 () () n nn n n n n − = − − − − −− − 3 ( ) 3 3 3 ( ) 2 ( 1) ( 2) ε ε δδ δ ( ) ( ) 3 12 2 3 2 1 z z zz z ↔ ⋅ −− − − −− − ( ) 2 2 4 3 1 z z z − = − ， z >1 例6.2 求下列信号的单边 z 变换，并标明相应的收敛域。 （a） ( ) ( 4) ( 4) ( ) 3 ( ) n x nn n n n = ++ −+ + − δ δ δε （b） 1 ( ) ( 3) 2 n xn n ε   = +     解 这种题解答过程并不复杂，只是要求审题细心，正确理解单边变换的概念，明确 n 的取 值范围是 n ≥ 0。 （a）由定义式 [ ] 0 0 4 4 () () ( 4) ( 4) ( ) 3 ( ) 11 2 , 0 n n n n n xn xnz n n n nz z zz ξ δ δ δε ∞ − = ∞ − = − − = = ++ −+ + −     = ++= + > ∑ ∑ （b） [ ] 0 0 1 1 ( ) ( 3) 2 1 ( ) 2 1 1 , || 1 1 3 1 3 3 n n n n n n xn n z n z z z z z ξ ε ε ∞ − = ∞ − = −   = +       =     == > − − ∑ ∑ 例6.3 求下列序列的变换，并指出收敛域

CAUCIEE(a) ()()(b) x(n)=2"cosn-6(n)解 (a) ()=(--() (-n-D)+()c(-1)因为[ -]-[]- ]21-3利用微分特性(-)同理[(-]--[司](jy/=k3因此3-k35[x(m)]=7(- (-)(b) x(n)=2"cosn~-6(n)解这类题目常用的方法是将x(1)为成指数函数形式或利用z域尺度变换公式。利用z域尺度变换公式[()]-x()

CIEE CAU （a） | | 1 () | | 3 n xn n   =     （b） ( ) 2 cos ( ) 4 n x n nn π = ⋅ε 解 （a） | | 11 1 ( ) | | ( 1) ( 1) 33 3 nn n xn n n n n n ε ε −    = =− − − + −       因为 1 1 1 11 ( 1) ( 1) 3 33 1 1 1 3 , || 3 3 1 1 3 3 n n n n z z z z z ξε ξ ε − −         −= −        == > − − 利用微分特性 2 1 1 3 ( 1) 3 1 3 1 3 1 , || 1 3 3 n d nn z dz z z z z ξ ε             − =−           −   = >     −   同理 ( )2 1 ( 1) 3 3 3 , ||3 3 n d z n nz dz z z z z ξ ε −        − − − =−        −   = < − 因此 [ ] ( )2 2 1 3 1 3 () , | | 3 3 1 3 3 z z xn z z z ξ = + << −     −   （b） ( ) 2 cos ( ) 4 n x n nn π = ⋅ε 解这类题目常用的方法是将 x( ) n 为成指数函数形式或利用 z 域尺度变换公式。 利用 z 域尺度变换公式 1 1 ( ) n z ax n X a ξ       =    

CAUCIE由于x(n)=cos≤n-e(m)5[(m) = X(-)=5[cos=n: (n))2-COs=>12-V22+12-22cos+1所以5[x(m) =5[2"x(m]=x()=X()则(-)≥(=- V2)>1[>2X(=)=2V2=+4()-/2×+1例6.4若0-(1) 0)试确定两个不同的序列，每个序列都有其变换，且满足：(1) Y(=)=[X(a)+X(-)]（2）在平面内，X()仅有一个极点和一个零点。解由于-() s)则，≤[(n)] = Y(2) :1-16--16Y(2*)=公+1+2+云令X(a)==乎

CIEE CAU 由于 1 ( ) cos ( ) 4 x n nn π = ⋅ε [ ] 1 1 2 2 2 ( ) ( ) cos ( ) 4 2 cos 2 4 , | |1 2 1 2 cos 1 4 xn X z n n z z z z z z z z z π ξ ξε π π   == ⋅         − −   == > − + − + 所以 [ ] () 2 () 1 1 ( ) 2 n z ξ ξ x n xn X Xz   = ==         则 ( ) ( ) 2 2 2 22 2 2 22 4 2 1 2 2 z z z z X z z z z z        −   −   = =   − +   − ×+   1 2 2 z > > 或 z 例6.4 若 1 () () 16 n yn n ε   =     试确定两个不同的序列，每个序列都有其变换 ，且满足： （1） [ ] 2 1 ( ) ( ) ( ); 2 Yz Xz X z = +− （2） 在平面内， X ( )z 仅有一个极点和一个零点。 解 由于 1 () () 16 n yn n ε   =     则 [ ] 1 1 1 () () , 1 1 16 1 16 16 z yn Y z z z z ξ − == = > − − 2 2 2 1 ( ) 1 11 2 16 4 4 z zz Y z z zz     == +   − −+     令 1 1 () , 1 4 4 z Xz z z = > −

CAUCIEEX(=)有零点，==0和极点≥=一，满足条件（2)，且[X(3)+X(-)]--Y(-2)满足条件（1)），所以[x()=(m)-() s(n)为所求的第一个序列。同理，令X,(a)=-京极点==，零点2=0x(0+x(=Y(2*)A(m)=[x()]-(-) c(0)于是[e(mn)和x(mn)=(1-) e(n)(n)为所求的二个序列。例6.5已知X(a)=乎>212-2L-

CIEE CAU 1 X ( )z 有零点， z = 0和极点 1 4 z = ，满足条件（2），且 [ ] 2 1 11 () ( ) 2 2 1 1 4 4 1 2 1 1 4 4 ( ) z Xz X z z z z z z z Y z    −  +−= −    − −−        = +    − +    = 满足条件（1），所以 [ ] 1 1 1 1 () () () 4 n ξ X z xn n ε −   = =     为所求的第一个序列。同理，令 2 1 () , 1 4 4 z Xz z z = > + 极点 1 4 z = − ，零点 z = 0 [ ] 2 2 2 1 1 () ( ) 2 2 1 1 4 4 1 2 1 1 4 4 ( ) z z Xz X z z z z z z z Y z    −  + −= +    + −+        = +    − +    = 则 [ ] 1 2 2 1 () () () 4 n x n Xz n ξ ε −   = =−    于是 1 1 () () 4 n x n n ε   =     和 2 1 () 1 () 4 n x n n ε   = −     为所求的二个序列。 例6.5 已知 1 1 2 1 1 3 () , 2 1 2 z Xz z z z − − − − = > + −

CAUCIE求x(2)的反变换x(n)。解在此用部分分式展开法求解。由11-1-X()-+-2.*(@+1-2)_ +“(=-1)(2+2) ++2用留数方法求系数A，B，艮4[2-(-] -[42-(+2]-于是22-2X(a)=:2-1 z+2因为收敛域>2，故[22+量[2+7(-2]()x(n)=5-[X(=)]=52例6.6利用部分分式展开法求X(0-%>4的逆变换x(n)。解具有多重极点的例子是经常出现的，求其逆变换的过程相对复杂一些。将X(a)展开成>形式，即-4X()++其中-[x0(-][--于是

CIEE CAU 求 X ( )z 的反变换 x( ) n 。 解 在此用部分分式展开法求解。由 1 1 22 1 1 1 () 3 3 ( ) 1 2 ( 2) z zz X z z z zz − − − − − = = + − +− 1 ( ) 3 ( ) ( 1)( 2) 1 2 z z X zAB zz zz z − = =+ − + −+ 用留数方法求系数 A，B，即 1 () 2 ( 1) z 9 X z A z z =   = ⋅− =     2 () 7 ( 2) z 9 X z B z z =−   = ⋅+ =     于是 2 7 9 9 ( ) 1 2 z z X z z z = + − + 因为收敛域 z > 2 ，故 [ ] 1 1 2 7 9 9 1 ( ) ( ) 2 7( 2) ( ) 1 29 n z z x n Xz n z z ξξ ε − −     = = + = +−       − +     例6.6 利用部分分式展开法求 3 3 8 () , 4 ( 4) z z Xz z z − = > − 的逆变换 x( ) n 。 解 具有多重极点的例子是经常出现的，求其逆变换的过程相对复杂一些。 将 X ( )z 展开成 3 1 ( 4) j j j j c z = z − ∑ 形式，即 2 3 1 2 3 2 3 ( ) ( 4) ( 4) ( 4) cz c z c z X z zz z =+ + −− − 其中 3 3 3 3 4 4 4 81 ( ) 2 z z z zz c Xz z z = =      − − =⋅ = =              于是

CIEECAUG(=-4) +C2(=-4)+→-X(a)=(2- 4)(G +c, +c) (8 +4c.)2* +16c=_ -8(2-4)(z-4)比较系数Je+c,+=1 或 8c,+4c,=0[16c, =-8得以上方程组得C, =G=-2则11X(a)={=>4-4*(-4)*(=-4)利用公式(μ+1)(n+2) (n+m)a -c(m)(=-a)m+1得+-4++(+)+++2.()x(n)=2×2×l=(n2 +7n+4).4-l. (n)例6.7利用≥变换求解差分方程(n+2)+ y(n+1)-6y(n)=x(n+1)y(0) =0, y(1)=1x(n)=4"e(n)利用单边≥变换对题中给定的差分方程求单边：变换2[Y(2) -(0) - y(1)=) ]+2[Y(2) - (0)] -6Y(2)= [X(-) - x(0)] 代入初始值y(0)=0,(1)=1和x(0)=1，有2[Y(2)-2"]+2Y(2)-6Y(-)=2X()-2整理得

CIEE CAU 22 3 1 2 3 1 ( 4) ( 4) 2 ( ) ( 4) cz z c z z z X z z − + −+ = − 3 2 3 123 1 2 1 3 3 ( ) (8 4 ) 16 8 ( 4) ( 4) c c c z c c z cz z z z z ++ − + + − = = − − 比较系数 12 1 2 1 1 1 84 0 2 16 8 cc c c c   + += + =    = − 或 得以上方程组得 1 2 1 , 1 2 c c = − = 则 3 2 2 3 1 1 2 2 () 4 4 ( 4) ( 4) z z z Xz z zz z − =+ + > −− − 利用公式 ( ) 1 1 1 ( 1)( 2) ( ) ( ) ! m n m z n n nm a n z a m ξ ε + − +   ++ +   = ⋅   −   L 得 1 ( 1)( 2) 4 ( ) 4 ( 1) 4 ( ) 2 221 n n n n x nn n ε   + + =− ⋅ + + + ⋅     × × 2 1 ( 7 4) 4 ( ) n nn n ε − = + +⋅ ⋅ 例 6.7 利用 z 变换求解差分方程 ( 2) ( 1) 6 ( ) ( 1) (0) 0, (1) 1 () 4 () n yn yn yn xn y y xn n ε + + +− = + = = = 解 利用单边 z 变换对题中给定的差分方程求单边 z 变换 [ ] 2 1 z Y z y y z zY z y Y z ( ) (0) (1) ( ) (0) 6 ( ) −   −− + − −   = − zXz x [ ] ( ) (0) 代入初始值 y y (0) 0, (1) 1 = = 和 x(0) 1 = ，有 2 1 z Y z z zY z Y z zX z z () () 6 () () −   −+ − = −   整理得

CAUCIEE(3*+2-6)(0)=2·X(2)由x(n)= 4'c(n)得X()=-4>4则YO7-2“(=-2)(++3)(=-4)其中-[(-2] [] -[些(+3] [--] --[-(-] ] -则YO>4所以-(-2"-(-3)+号-4)(m)例6.8对于输入为x(n)输出为y(n)的线性非移变系统，已知:(1)若对于所有n，x(n)=(-2)，则对于所有n，J(n)=0;=() (m);则对于所有n， Ym)为(2)若对于所有n：x(m)-()以m)=6()+a()e(m)， 其中a 是一个常数

CIEE CAU ( ) 2 z z Yz zXz +− =⋅ 6 () () 由 () 4 () n x n n = ε 得 () 4 4 z Xz z z = > − 则 2 ( ) 6 4 z z Y z zz z = ⋅ + − − ( )( )( ) 2 234 z zzz = − + − 1 2 3 ( ) 234 Y z c c c zz z z =++ − + − 其中 ( ) ( )( ) 2 2 1 () 1 2 34 5 z z Yz z c z z zz = =     = ⋅− = =       + −   ( ) ( )( ) 3 3 2 () 3 3 2 4 35 z z Yz z c z z zz =− =−     = ⋅ + = =−       − −   ( ) ( )( ) 4 4 3 () 2 4 23 7 z z Yz z c z z zz = =     = ⋅− = =       − +   则 232 5 35 7 () 4 234 z zz Yz z zzz =−+ > −+− 所以 ( ) 23 2 () 2 3 4 () 5 35 7 n n n yn n ε   = ⋅ − − +⋅     例 6.8 对于输入为 x( ) n 输出为 y n( ) 的线性非移变系统，已知： （1）若对于所有 n， () 2 ( )n x n = − ，则对于所有 n， y n() 0 = ； （2）若对于所有 n， 1 () () 2 n x n n ε   =     ，则对于所有 n， y n( ) 为 1 () () () 4 n yn n a n δ ε   = +     ，其中 a 是一个常数

CIEECAU(a)求常数α的值；(b）如果对于所有n，x(n)=1，求响应y(n)。解（a）由已知条件(=)得，X(2) =5[x(0)]-1Y(-)=5[(0)]=1+-2-4则1+()- -京由已知条件（1)，x(n)=(-2)"为特征函数，则输出(m) -(-2) - (-).--=0即1+ 2(-2)-2-14=0H(-2) = -22或1+%=04于是α-(b）当输入x(n)=1时，+=0(n)=1* H(-)-= H()=-=-212例6.9研究一个LSI系统，其输入x(n)和输出y(n)满足

CIEE CAU (a)求常数 a 的值； （b）如果对于所有 n， x n() 1 = ，求响应 y n( ) 。 解 （a） 由已知条件( )z 得， [ ] [ ] 1 () () | | 1 2 2 1 () () 1 | | 1 4 4 z X z xn z z az Y z yn z z ξ ξ == > − = =+ > − 则 1 1 ( ) 4 ( ) ( ) 1 2 az z Y z H z X z z z + − = = − 由已知条件（1）， () 2 ( )n x n = − 为特征函数，则输出 ( ) 2 () 2 () 0 n z yn H z =− = −⋅ = 即 ( 2) 1 1 2 4 ( 2) 0 2 1 2 2 a H − + − − − = = − − − 或 2 1 0 9 4 a + = 于是 9 8 a = − （b）当输入 x n() 1 = 时， 1 9 1 8 1 0 1 1 4 1 ( ) 1 ( ) (1) 1 4 1 1 2 n z yn H z H = − ⋅ + = − = ⋅ = = =− − 例 6.9 研究一个 LSI 系统，其输入 x( ) n 和输出 y n( ) 满足

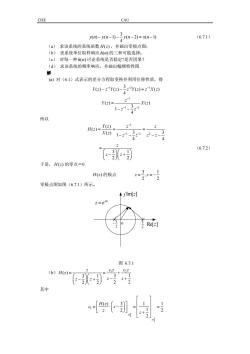
(6.7.1)(n)-y(n-1)-=y(n-2)=x(n-1)(a）求该系统的系统函数H()，并画出零极点图(b）求系统单位取样响应h(n)的三种可能选择：(c）对每一种 h(n)讨论系统是否稳定?是否因果？（d）求该系统的频率响应，并画出幅频特性图(@）对（6.1）式表示的差分方程取变换并利用位移性质，得Y()-"(a)---Y(=)=:X()-Y(=)X(=)所以H(2) - Y() ,X()1-21-2---(6.7.2)(-)于是，H(=)的零点="="-H()的极点零极点图如图（6.7.1）所示。 j Im[3]Re[]图 6.7.1(b)H(=)）其中=/H(.(2-3)

CIEE CAU 3 ( ) ( 1) ( 2) ( 1) 4 yn yn yn xn − −− − = − （6.7.1） （a） 求该系统的系统函数 H z( ) ，并画出零极点图； （b） 求系统单位取样响应 h n( ) 的三种可能选择； （c） 对每一种 h n( ) 讨论系统是否稳定?是否因果？ （d） 求该系统的频率响应，并画出幅频特性图. 解 (a) 对（6.1）式表示的差分方程取变换并利用位移性质，得 1 21 3 () () () () 4 Yz zYz z Yz z Xz − −− −− = 1 1 2 () () 3 1 4 z Yz Xz z z − − − = − − 所以 1 1 22 ( ) ( ) ( ) 3 3 1 4 4 Yz z z H z X z z z zz − − − == = − − −− 3 1 2 2 z z z =       − +    （6.7.2） 于是， H z( ) 的零点＝0 H z( ) 的极点 3 1 , 2 2 z z = = − 零极点图如图（6.7.1）所示。 图 9.10.1 1 2 − O 3 2 j z e ω = j z Im[ ] Re[ ]z 图 6.7.1 （b） 1 2 ( ) 3 1 3 1 2 2 2 2 z cz c z H z z z z z = =+    − + − +       其中 3 2 3 2 1 () 3 1 1 2 2 1 2 z z H z c z z z = =         = ⋅− = =             +  