《信号与系统》课程授课教案（课件讲稿）第3章 离散系统的时域分析

第三章离散系统的时域分析阶差分"()=VIV(k)=V(k)-(k-1I)8 3-1 离散系统的响应=Vf(k)-Vf(k-1)连续系统离散系统相似性= f(k)-2f(k-1)+ f(k -2)微分方程差分方程求解方法对应差分方程的一般形式卷积积分卷积和同等重要地位F[k, y(k),Vy(k),...,v"y(k)l=0一。 差分与差分方程 4(k) (k+1)-(k)一阶前向差分G[k, y(k),y(k -1),, y(k - n)]= 0阶后向差分V()~ ()-(-1)n阶常系数线性系统方程三、选代解法：利用前一时刻的函数值递n阶后向差分方程：推得到当前时刻的函数值y(k)+an--y(k-1)+..+aoy(k-n)例: (n)-(n-1)-y(n-2)=8(n)=bm(k)+bm1J(k-1).+bo./(k-m)y(-1) = 0y(-2) = 0知an =1解：为便于迭代，移项：a.-v(k-i)f(k-)y(n)=8(n)+ y(n-1)+ y(n-2)n阶前向差分方程：J(0)= 8(0) + (-1) + y(-2) =1(*+)-b(k+y(1)=1+ y(0)+ y(-1)=2基本运算单元J(2)=1+ y(1)+ y(0) = 4x(k)+x(k)x():①加法器x(hTJ(n)={0.0,1247,12. ]k=0a②乘法器 x(k)--ax(k)注：这种解法虽不容易得到闭式解，但简明易行，便于用计算机进行求解。D③延时器(k)x(k-1)三.离散系统的模拟

1 第三章 离散系统的时域分析 §3-1 离散系统的响应 一．差分与差分方程 微分方程 差分方程 求解方法对应 连续系统 离散系统 相似性 卷积积分 卷积和 同等重要地位 ∆f (k) f (k +1) − f (k) def 一阶前向差分 ∇f (k) f (k) − f (k −1) def 一阶后向差分 ( ) [ ( )] [ ( ) ( 1)] 2 二阶差分 ∇ f k = ∇ ∇f k = ∇ f k − f k − = ∇f (k) − ∇f (k − 1) = f (k) − 2 f (k − 1) + f (k − 2) F [k , y(k ), ∇ y(k ), ,∇ y(k )] = 0 " n 差分方程的一般形式 G[k, y(k), y(k − 1),", y(k − n)] = 0 或 ( ) ( 1) ( ) y k + an−1 y k − +"+ a0 y k − n ( ) ( 1) ( ) = bm f k + bm−1 f k − "+ b0 f k − m n阶前向差分方程： n阶常系数线性系统方程 ∑ ∑ = = + = + m j j n i i a y k i b f k j 0 0 ( ) ( ) ∑ ∑= − = − − = − m j m j n i n i a y k i b f k j 0 0 ( ) ( ) n阶后向差分方程： = 1 n a 后向差分方程 多用于因果系统 前向差分方程 多用于状态方程 二、迭代解法：利用前一时刻的函数值递 推得到当前时刻的函数值 例： y(n) − y(n − 1) − y(n − 2) = ε (n) 知 y(−1) = 0 y(−2) = 0 解：为便于迭代，移项： y(n) = ε (n) + y(n − 1) + y(n − 2) y(0) = ε (0) + y(−1) + y(−2) = 1 y(1) = 1+ y(0) + y(−1) = 2 y(2) =1+ y(1) + y(0) = 4 # 注：这种解法虽不容易得到闭式解，但 简明易行，便于用计算机进行求解。 三.离散系统的模拟 y(n)={0,0,1,2,4,7,12,"} k=0 ( ) 1x k ∑ ( ) ( ) 1 2 x k +x k ( ) 2 x k + ①加法器 + 基本运算单元 ③延时器 x(k) D x(k−1) ②乘法器 x(k) a ax(k)

例1：四.经典法J(k)= f(k)+ ay(k-1)f(k)+n阶后向差分方程：y(k)any(k)+ an-iy(k -1)+..+aoy(k-n)aDy(k-1)=bmJ(k)+bm--f(k-1)+.+baf(k-m)例2:(k+1)=a(k)+ f(k)_(k)-=D(k+1)-(k)解由齐次解和特解组成?Dy(k)y(k)= yh(k)+ y,(k)f(k)a1.齐次解：yr（k）y(k)+an-)(k-1)+.+ay(k-n)=0①一阶齐次方程(k)具有C的形式，代人方程y(k)+aij(k-1)=0后项=常数Cak +Can--ak-l +.+Caak-" =0J()-前项:C±0zk-n￥0方程两边同除以Cak-J(k-1)y(k)是一个公比值为（-a,)的几何级数得 "+an--a"-++a,a +a =0yr(k)=C(-α)特征方程②n阶齐次方程特征根A1,A2,...An则(k)=C,+C,鸡+.+C,,为共轭复根,个不相等的实根A, =a+bj=aeio a, =a-bj=ae-ioy(k)=C,+C,+.+C,,为重根y(k) = α* (C cos ko + D sin k0)二阶：J(k)=(CI +C,k)ah阶:y(k)=(Cy-1kr-*+C,-2kr-2 +.+C,k+Co)2

2 y(k) = f (k) + ay(k − 1) 例1： y(k −1) f (k) + ∑ D a + + ∑ f (k) D a + y(k +1) = ay(k)+ f(k) [ ( 1) ( )] 1 ( ) y k f k a 例 y k = + − 2： y(k) y(k) ( ) ( 1) ( ) an y k + an−1 y k − +"+ a0 y k − n ( ) ( 1) ( ) = bm f k + bm−1 f k − +"+ b0 f k − m 四. 经典法 n阶后向差分方程： 解由齐次解和特解组成 y(k) y (k) y (k) = h + p k yh(k) C( a ) = − 1 y(k) + a1 y(k − 1) = 0 ①一阶齐次方程 y ( k ) 1. 齐次解： h 1 ( 1) ( ) a y k y k =− − 常数 前项 后项= y(k)是一个公比值为（-a1)的几何级数 ②n阶齐次方程 0 0 1 + 1 + + = − − − k k n n k Cλ Ca λ " Ca λ y(k) k 具有 的形式，代入方程 Cλ k n k n C C − − ∵ ≠ 0 λ ≠ 0 方程两边同除以 λ 1 0 0 1 + 1 + + + = − a − a a n n n 得 λ λ " λ 特征方程 特征根 λ1,λ 2,"λn y(k)+ an−1 y(k −1)+"+ a0 y(k − n) = 0 k n n k k 则 y(k) = C1λ1 + C2λ2 +"+ C λ k n n k k y(k) = C1λ1 + C2λ2 +"+ C λ k i 二阶： y ( k ) = (C 1 + C 2 k )λ k C i y k C k C k C k λ γ γ γ γ ( ) ( ) 1 0 2 2 1 = 1 + + + + − − − − " γ阶： a.λi为 n个不相等的实根 b λi为重根 y(k ) α (C cos kθ D sin kθ ) k = + θ λ α j i = a + bj = e θ λ α j j a bj e − = − = 为共轭复根 i j c, λ , λ λi λ j

2.特解3.全解（给定初始条件下的定解）y,(k)(k)y(k)= yh(k)+ y,(k)P.k"+P..k++P+P *1km特征根为单根=1为重根[P."Pk+PKPd2,±aakJ(k)-Ec, +y,(k)[Pk+ P,]ak4=a,单根i=1=C,+C++C,a+y,(k)cos( Bk)Pcos Pk+Qsin βk*eti或sin(Bk)y(0), y(1),.*,y(n -1) -→ C1,C2,.,Cn.举例例1求齐次方程的解例：由上式（单根）J()-2(k-1)+2)(k-2)-2)(k-3)+2)(k-4)=0y(0)=CI+C, +.+C. + y,(0)[巨知 ()=1 (2)=0 (3)=1 (4)=1y(1)=a,C +a,C, +.+a,Cn + y,(1)解：特征方程，:4-23+22-2+1=0J(n-1)=C+2'C,++C, +y,(n-1)(α - 1)2(a2 +1) = 0 = = 1=j=-可唯一解出.C,(k)=(Ck+C)(1)+Ccos元+Dsin元y(k)=1+cos由初始条件Ci+C2 + D =1例2求差分方程的解2C +C2 -C= 0y(k)+4y(k -1)+4y(k -2) = 2*(k ≥0)3C, +C, -D=1巨知y(0)=0y(1) =-14C, +C, +C =1解：①齐次解rC; =0+4a+4=0C, =1D=0=M =-2故LC=1y,(k)=(Ck+C)(-2)

3 γ P k Pk P k m m [ ] +"+ 1 + 0 λi = 1为γ重根 ≠ 1 λi m k 1 0 1 P k P 1k Pk P m m m m + + + + − − " k a k Pa a λi ≠ k [P k P ]a 1 + 0 λi = a,单根 Pcos βk + Qsin βk β λ j e± i ≠ cos( βk ) 或sin(βk) y (k ) f (k ) p 2.特解 ( ) ( ) 1 y k C y p k n i k ∑ i i = = λ + 3.全解（给定初始条件下的定解） y(k) y (k) y (k) = h + p 特征根为单根 ( ) 1 1 2 2 C C C y k p k n n k k = λ + λ +"+ λ + n C C Cn y(0), y(1), , y( 1) , , , " − → 1 2 " # (0) (0) 1 2 n p y = C + C + " + C + y (1) (1) 1 1 2 2 n n p y = λ C + λ C + " + λ C + y ( 1) ( 1) 1 2 1 1 2 1 − = 1 + + + + − − − − y n C C Cn yp n n n n n λ λ " λ 例：由上式（单根） 可唯一解出 C1"Cn ( 1) ( 1) 0 2 2 λ − λ + = = = = j = − j 1 2 3 4 λ λ 1 λ λ π π 1 2 2 2 ( ) ( )(1) cos sin k k k ∴ y k = C k + C + C + D y(1) = 1 y(2) = 0 y(3) = 1 y(4) = 1 y(k)−2y(k−1)+2y(k−2)−2y(k−3)+2y(k−4)=0 例1求齐次方程的解 巳知 2 2 2 1 0 4 3 2 λ − λ + λ − λ + = 解：特征方程， 4. 举例 C1 = 0 C2 = 1 D = 0 C = 1 3C1 + C2 − D = 1 C1 + C2 + D = 1 2 0 C1 + C2 − C = 4C1 + C2 + C = 1 由初始条件 2 ( ) 1 cos kπ y k = + 4 4 0 2 λ + λ + = ∴ λ1 = λ2 = −2 y(k) + 4 y(k − 1) + 4 y(k − 2) = 2 (k ≥ 0) k y(0) = 0 y(1) = −1 例2求差分方程 巳知 的解 解：①齐次解 k yh(k) (C k C )( 2) 故 = 1 + 2 −

②特解代入初始条件：特解形式为y,(k)=p(2)代入差分方程y(0)= C, +P(2)* +4p(2)-I + 4p(2)-2 =2ky(1) = -2Cf - 2C得p=1得C =1,C, =-y,(k)=1(2)<全解为：(k)=(k-)(-2)* +(2)t特解的形式③全解1自由响应强迫响应J(k)=(Gk+G)(-2)* +(2)y(k)= yr(k)+ y,(k)五、零输入响应和零状态响应①初始值的分解如果k=0时激励接入零输入响应：1、设Jf(-1)= Jf(-2)=..= yr(-n)= 0(k)+au--j(k-1)+..+ao(k-n)= f(k)J+(-1)= (-1),y(-2)=(-2),y(-n)=(n)初始状态：(-1),y(-2),y(-n)@y (k)y.(k)+a.-y.(k-1)+.-+aoy(k-n)=01y(-I),y(-2)(-n)设特征根为，2，nCx" +C2"+C=y(-1)=(-1)yr(k)=Cra, +Cr2a, +...Cnah:Cm +C2* +C =y(-2)=(-2)求初始值C"+Cn"+..Cxa"=yr(-n)=y(-n)yr(0),y.(1),yx(2),,yr(n- I):J.(k)=-a-y(k-1)-..ay(k-n)-Cx,C x2,.. C xn将0,1,2，，n-1代入即可

4 4 1 得 p= ②特解 k p 特解形式为 y (k)= p(2) k k k k p(2) 4 p(2) 4 p(2) 2 1 2 + + = − − k y p k (2) 4 1 ( ) = 特解的形式 代入差分方程 k k y k C k C (2) 4 1 ( ) ( )( 2) = 1 + 2 − + ③全解 0 4 1 (0 ) y = C 2 + = 2 1 4 1 (1) 2 2 y = − C 1 − C 2 + × = − 代入初始条件： 4 1 1, 得 C1 = C2 = − k k y k k (2) 4 1 )( 2) 4 1 全解为： ( ) = ( − − + 自由响应 强迫响应 五、 零输入响应和零状态响应 1、 零输入响应： ( ) ( 1) ( ) ( ) 1 0 y k a y k a y k n f k 设 + n− − +"+ − = 初始状态：y(−1), y(−2)," y(−n) y f (−1) = y f (−2) = " = y f (−n) = 0 y ( 1) y( 1), y ( 2) y( 2), y ( n) y( n) x − = − x − = − " x − = − y (k) ② x ①初始值的分解 如果 k = 0时激励接入 y ( 1),y ( 2), y ( n) x − x − " x − ( ) ( 1) ( ) 0 yx k +an−1 yx k − +"+a0 yx k −n = y(k ) y (k ) y (k ) = x + f k xn n k x k ∴ y x (k ) = C x 1λ 1 + C 2λ 2 + "C λ λ λ " λ n , , 设特征根为 1 2 求初始值 ( ) ( 1) ( ) ∵ yx k = −an−1 yx k − −"−a0 yx k −n 将0，1，2，"，n − 1代入即可 y (0), y (1), y (2), , y (n − 1) x x x " x C x C x " C xn , , 1 2 ( 1) ( 1) 1 1 2 2 1 1 1 + + = − = − − − − C C C y y x λ x λ " xnλ n x ( 2) ( 2) 2 2 2 2 2 1 1 + + = − = − − − − C C C y y x λ x λ " xnλ n x ( ) ( ) C 1 1 C 2 2 C yx n y n n xn n n x n x + + = − = − − − − λ λ " λ #

2、零状态响应[y,(k)+a,-y,(k-1)++y,(k-n)=f(k)1 y/(-1)=y,(-2)=y/(-3) .=y)(-n)=02c++, 0)yy(k)=ECat + y,(k)求初始值Zcha-+y,(n-1)= y(n-1)y(k)=-an-1yf(k-1)--aoy (k-n)+f(k)= C f1Cf2,.. C m将0,1,2,，n-1代入,得,(O), yr(1),y,(2)-y (n-1)3、全响应例、差分方程[ (k)+-(k-1)++)(k-m)= (k)y(k)+3y(k -1)+2y(k -2)=2 u(k)J(-1),J(-2),(-3)-*(-n)L y(-1) = 0, 3(-2)- (k)= yr(k)+ y (k)求零输入响应、零状态响应、全响应。Ec,a +y,(k)解：①零输入响应Cianat+y,(k)零输入响应零状态响应特征方程J,(k)=P.2h特解22 +3 +2=0代入差分方程1f = -1,22 =-2(k)-I(2)k≥0Jx(k)=Cx1(-1)* +Cr2(-2)k[()=Cn(-1)*+Cn(-2)+(2)[代:(-1)=0, (-2)=Lyr(-1)=0, yr(-2)=0→Cx1=1;C2 = -2Cn=;C2=1故y(k)=(-1)*+(-2)+1k≥0,(k)=-+(-1)* +(-2)*+(2)：②零状态响应

5 ( ) ( 1) ( ) ( ) yf k +an−1 yf k − +"+a0 yf k −n = f k yf (−1)= yf (−2)= yf (−3)"= yf (−n)=0 ( ) ( ) 1 y k C y k p n i k f = ∑ fi i + = ∵ λ 2、 零状态响应 求初始值 将0，1，2，"，n − 1代入,得 ( ) ( 1) ( ) ( ) 1 0 y k a y k a y k n f k f = − n− f − −"− f − + y (0) y (1), y (2) , y (n − 1) f ， f f " f (0) (0) 1 C y y p n i ∑ fi + = = (1) (1) 1 C y y p n i ∑ fi i + = = λ ( 1) ( 1) 1 1 ∑ + − = − = − C y p n y n n i n fi λ i # C f C f " C fn , , ⇒ 1 2 ( ) ( 1) ( ) ( ) y k + an−1 y k − +"+ a0 y k − n = f k y(−1), y(−2), y(−3)"y(−n) ( ) 1 C y p k n i k = ∑ i i + = λ y(k ) y (k ) y (k ) = x + f ( ) 1 1 C C y k p n i k fi i n i k = ∑ xi i + ∑ + = = λ λ 零输入响应 零状态响应 3、 全响应 例、差分方程 y(k) 3 y(k 1) 2 y(k 2) 2 u(k) k + − + − = 2 1 y ( − 1) = 0 , y (− 2 ) = 求零输入响应、零状态响应、全响应。 解：①零输入响应 y (k ) = C 1 (−1) + C 2 (−2) k ≥ 0 k x k x x λ1 = −1,λ 2 = −2 1; 2 ⇒ Cx1 = C x 2 = − 3 2 0 2 λ + λ + = 特征方程 2 1 代入 y x (−1) = 0, y x (−2) = ②零状态响应 ( ) ( 1) ( 2) 0 1 = − + − ≥ + y k k k k 故 x k p y k (2) 3 1 ( ) = k 特解 y p (k) = P ⋅ 2 代入差分方程 k k f k y f k C f C (2) 3 1 ( ) ( 1) ( 2) = 1 − + 2 − + (−1) = 0, (−2) = 0 f f y y ; 1 3 1 ⇒ C f 1 = − C f 2 = k k k f y k (2) 3 1 ( 1) ( 2) 3 1 ∴ ( ) = − − + − +

③全响应:k=08(k)=1y(k)=y (k)+yt(k)8(k)=0k>0:: k>0h(k)形式同零输入形式号(-1)* -(-2) +(2)*例：求图示离散的单位样值响应h(k)$3-2单位序列响应（单位样值响应)+ y(k)K-Dh(k)k+?J(k-2)(k)定义：零状态DTk=018(k)=L0k±0:8(0)=18(1) =0解：①列写差分方程，求初始值:h(0=h(-D±2h(-2)+8(0)=1加法器输出：h(1)= h(0)+ 2h(-1)+ 8(1) =1y(k)= y(k-1)+2y(k -2)+ f(k)②求h(k)y(k)- y(k -1)-2y(k -2)= f(k)或：k>0 rh(k)-h(k-1)-2h(k-2)=0单位样值响应：[ h(0)=1 h(1)=1 h(k)-h(k-1)-2h(k-2)=8(k)特征方程[L h(-1)=h(-2) =0 --2=(+1)(-2)=0求初始值卷积和$3-3特征根, = -1,X, = 2齐次解h(k)=C,(-1) +C2(2),k>0连续系统由初始值：h(0)=C, +C, =1yr(t)= f(t)*h(t)= f' s(0)h(t-t)dth(1)= -Ct+ 2C, = 1f(k)r(k)离散系统离散 G C-零状态-1(-1* +(2),故基本方法：分解，分别作用，合成h(k)=3k≥0

6 y(k ) y (k ) y (k ) = x + f k k k (2) 3 1 ( 1) ( 2) 3 2 = − − − + ③ 全响应 §3-2单位序列响应（单位样值响应） δ (k) = 0 0 1 0 ≠ = k k δ(k) 定义： h(k) 零状态 ∵k = 0 δ (k ) = 1 k > 0 δ (k) = 0 ∴ k > 0 h(k)形式同零输入形式 例：求图示离散的单位样值响应h(k) y(k−1) y(k−2) ∑ D D f (k) y(k) + + + 2 1 y(k ) = y(k − 1) + 2 y(k − 2) + f (k ) h(k) − h(k − 1) − 2h(k − 2) = δ (k) h(−1) = h(−2) = 0 解：①列写差分方程，求初始值 加法器输出： 或： y(k ) − y(k − 1) − 2 y(k − 2) = f (k ) 单位样值响应： 求初始值 ∴ h(0) = h(−1)+ 2h(−2)+δ(0) =1 h(1) = h(0) + 2h(−1) + δ (1) = 1 k > 0 h(k)− h(k −1)− 2h(k − 2) = 0 h(0) =1 h(1) =1 ②求h(k) ∵δ(0)=1 δ(1) = 0 2 ( 1)( 2) 0 2 λ − λ − = λ + λ − = 特征方程 3 1 C1 = 3 2 C2 = 1, 2 特征根 λ1 = − λ 2 = h(k ) = C1 (−1) + C2 (2) , k > 0 齐次解 k k (0) 1 h = C1 + C 2 = (1) 2 1 h = − C 1 + C 2 = 由初始值： (2) , 0 3 2 ( 1) 3 1 h(k) = − + k ≥ 故 k k f (t) y ( t ) f h(t) §3-3 卷积和 连续系统 ( t ) f ( t ) h( t ) f ( t )h( t τ )dτ t = ∗ = − ∫0 f y 离散系统 f ( k ) y ( k ) f 离散 零状态 基本方法：分解，分别作用，合成

一、卷积和k=if(k)F(0)8(k-1)= [r(0)其中:1、分解LOk+i2、分别作用激励响应h(k)(k)F(k)= f(0)(k)+(-1)8(k+1)+f(-2)8(k+2)+ 8(k-i)h(k-i)+ f(1)(k -1)+...+ f(i)8(k -i)+.f(i)8(k-i)f(i)h(k-i)Zr(0)6(k-1)3、合成一般f(k)= Zf()8(k-i)Zf(i)f(k-i)fi(k)* f2(k)=Zr(0)f(k-i)叠加原理、yr(k)=>f(i)h(k-i)讨论：Ef(i)h(k-i)①当f(k)为因果序列,k>0,fi(k)有意义(k)k)y(k)=)或：(k)*f(k)=2(0)(k-1)记为y(k)= f(k)*h(k)=h(k)*f(k)i=0②当f(k为因果序列K(k)*f(k)-2(i)2(k-1)fi(k)* f2(k) =E fi(i)f(k -i)③当/:(k), f,(k) 均为因果序列①折叠(0)→ (-i)k>0右移k< 0, fi(k) = f2(k)= 0移位(K-1) 一亡2差糖fi(k)* f2(k)=Zfi(i)f2(k -1)③相乘Ji(i)fe(k -i)1ed①叠加Efi()fe(k -i)二、 卷积和的求解1、图解法

7 f(k) = f(0)δ(k) + f (1)δ (k −1) +"+ f (i)δ (k − i) +" ∑ ∞ =−∞ = − i f (i)δ (k i) 一、卷积和 1、分解 f(k) k i + f(−1)δ(k+1)+ f(−2)δ(k+2)+" δ (k) h(k) δ (k − i) h(k − i) f (i)δ (k − i) f (i)h(k − i) f (i) k = i f (i)δ (k − i) = 0 k ≠ i 其中： 2、分别作用 激励 响应 3、合成 ∑ ∞ =−∞ = − i f(k) f(i)δ(k i) ∑ ∞ =−∞ = − i f y (k) f (i)h(k i) ∑ ∞ =−∞ = − i f f (k) y (k) f(i)h(k i) 或： h(k) 记为 y(k) = f (k) ∗ h(k) = h(k) ∗ f (k) 叠加原理 ∑ ∞ = −∞ ∗ = − i f (k ) f (k ) f (i) f (k i) 1 2 1 2 ∑ ∞ =−∞ = − i f (i)f (k i) 2 1 ∑ ∞ = ∗ = − 0 1 2 1 2 ( ) ( ) ( ) ( ) i f k f k f i f k i ①当f 1(k)为因果序列 , k > 0, f 1(k)有意义 一般 讨论： ②当f 2 (k )为因果序列 ∑= −∞ ∗ = − k i f ( k ) f ( k ) f (i ) f ( k i ) 1 2 1 2 0 , ( ) ( ) 0 k k k ②移位 ( ) ( ) 1 2 ③相乘 f i f k − i ∑ ( ) ( − ) 1 2 ④叠加 f i f k i

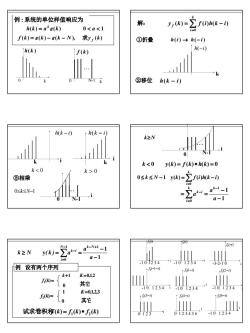
【例：系统的单位样值响应为解：r(k)=f(i)h(k -i)000≤k≤n-1 y(k)-Er(0)(k-i)③相乘-ak-l_10<k<N-1a-1f(-)N+k≥NAy(k)=a-1i=0-10·1234-10122321例 设有两个序列J(-1-1)f(1-1)f(2-1)K=0,1,2k+1()=Lo其它1012341-1012341234310r1K=0,1,2,3J(3-1)+ (4-1)(61)f(h= L0其它1试求卷积和(k)= f(k)*f;(k)-101234012345601123

8 h(k ) = a (k ) 0 0 k ③相乘 0 i " N-1 0≤k≤N−1 k≥N i " N-1 0 k < 0 y(k) = f (k)∗ h(k) = 0 ∑= ≤ ≤ − = − k i k N k f i h k i 0 0 1 y( ) ( ) ( ) 1 1 1 0 − − = = − = − ∑ a a a k k i k i 1 1 y 1 1 0 − − ≥ = = − − + = − ∑ a a k N ( k ) a N k N i k i 0 f1(k)= k+1 K=0,1,2 f2(k)= 1 K=0,1,2,3 0 ( ) ( ) ( ) 1 2 试求卷积和f k = f k ∗ f k 例 设有两个序列 其它 其它 ( ) 1 f i i -1 0 12 3 4 ( ) 2f i i -1 0 1 2 3 4 i (6 ) 2f −i -1 0 1 2 3 4 i ( ) 2f −i -3-2-1 0 i (2 ) 2f −i -1 0 1 2 3 4 i (1 ) 2f −i -1 0 1 2 3 4 (3 ) 2f −i i 0 1 2 3 i (4 ) 2f −i 0 1 2 3 4 5 6 i ( 1 ) 2f − −i -1 0 1 2 3 4

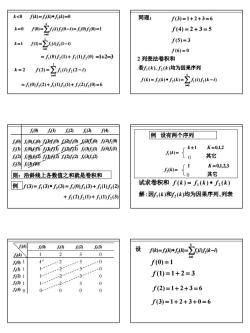
k<0(k)=f(k)*f(k)=0同理：f(3)=1+2+3=6k=0 (0)-(0)5(0-)=(0)(0)=1f(4)=2+3=5if(5) = 3(0)-2()(1-1)k=lf(6)=0f.(0)f(1)+ f.(1)f2(0) =1+2=32 列表法卷积和若fi(k),J(k)均为因果序列k=2f(2) =Zf(i)f(2-i)i=0(k)=(k)*()-(0)(-1)= f.(0).f(2)+ f.()f (1)+ f.(2)f2(0) =6f(0)f()f(2)J(3)(4)例设有两个序列( ((0) 2() L(2() (0) (4(0)K =0,1,2r k+1((0F) 5 2f (3)0) (40)J(k)=10其它(2) ((2 (2(2) (3)(2)(3) J(3) 40)K=0,1,2,3[1(k)=Lo其它则：沿斜线上各数值之和就是卷积和试求卷积和 f(k)=fi(k)*J(k)例(3)= f(3)* f(3)= fi(0)f(3)+ fi(1),f2(2)解:因fi(k)和f2(k)均为因果序列,列表+ f.(2)f2(1)+ Ji(1)2(3)i(f0)i(0)i(2)fi(3)设F()=f()*(M)-E(0)f(k-1)2301I1H0a1-2---0-3f(0) =1-0-2-3-f(1)=1+2= 3(2) 1人--3--02-(3) 130I-2--f(2)=1+2+3=6S(4 00---0。0f(3)=1+2+3+0=6

9 k<0 f(k)= f1(k)∗ f2(k)=0 0 (0) ( ) (0 ) (0) (0) 1 1 2 0 0 = =∑ 1 2 − = = = k f f i f i f f i ∑= = = − 1 0 1 2 1 (1) ( ) (1 ) i k f f i f i =1+2=3 ∑= = = − 2 0 1 2 2 (2) ( ) (2 ) i k f f i f i (0) (2) (1) (1) (2) (0) 6 = f1 f2 + f1 f2 + f1 f2 = (0) (1) (1) (0) 1 2 1 2 = f f + f f f (4) = 2 + 3 = 5 f (5) = 3 f (6) = 0 同理： f (3) = 1 + 2 + 3 = 6 ∑= = ∗ = − k i f k f k f k f i f k i 0 1 2 1 2 ( ) ( ) ( ) ( ) ( ) 若f1 (k ), f 2 (k )均为因果序列 2 列表法卷积和 (3) (0) (0) (2) (0) (1) (0) (0) 1 1 2 1 2 1 2 f f f f f f f f (1) (2) (1) (1) (1) (0) 1 2 1 2 1 2 f f f f f f (2) (2) (2) (1) (2) (0) 1 2 1 2 1 2 f f f f f f (3) (2) (3) (1) (3) (0) 1 2 1 2 1 2 f f f f f f (4) (1) (4) (0) 1 2 1 2 f f f f (3) (2) (1) (0) 2 2 2 2 f f f f (0) (1) (2) (3) (4) 1 1 1 1 f f f f f 则：沿斜线上各数值之和就是卷积和 (3) (3) (3) (0) (3) (1) (2) 1 2 1 2 1 2 例 f = f ∗ f = f f + f f (2) (1) (1) (3) 1 2 1 2 + f f + f f 0 f1(k) = k +1 K = 0,1,2 f2(k) = 1 K =0,1,2,3 0 ( ) ( ) ( ) 试求卷积和 f k = f1 k ∗ f 2 k 例 设有两个序列 其它 其它 解 :因f1 (k)和f 2 (k)均为因果序列,列表 0 1 1 1 1 1 0 1 1 1 1 0 2 2 2 2 2 0 3 3 3 3 3 0 0 0 0 0 0 (4) (3) (2) (1) (0) 2 2 2 2 2 f f f f f (0) (1) (2) (3) 1 1 1 1 f1(k) f f f f ( ) 2f k f (0) = 1 f (1) = 1 + 2 = 3 f (2) = 1 + 2 + 3 = 6 f (3) = 1 + 2 + 3 + 0 = 6 ∑= = ∗ = − k i f k f k f k f i f k i 0 1 2 1 2 设 ( ) ( ) ( ) ( ) ( )

三卷积和的性质Cok6④与单位样值函数的卷积和例1：已知复合系统由两个子系统级联而成，子系统的单位样值响应分别为h,(k)=a*s(k)由定义;f(k)*8(k)=f(h),hs(k)=b'e(k),求复合系统的 h(k)。(k)*8(k -k,)= f(k,)yr(k)J(k-k)*8(k-k2)= f(k-k; -k2)h(k)解:h(k)=h(k)*h(k)-a'e(i)-bk-e(k-iioa+ba=b=1h()-a(0)--(yε(k)* ε(k) = (k + 1)e(k)- 1-(g)+1bk+1 -ak+1=bε(k)1-()b-aa=bh(k)-Zb*(1) =b*2 (1) =(k+1)b*e(k)1=0=

10 f(k)= f1(k)∗ f2(k)= 0 3 5 6 6 3 1 0 6 5 4 3 2 1 0 0 > = = = = = = < k k k k k k k 即 k 三 卷积和的性质 ( ) ( ) ( ) ( ) f 1 k ∗ f 2 k = f 2 k ∗ f 1 k ①交换律 ( ) [ ( ) ( )] [ ( ) ( )] ( ) 1 2 3 1 2 3 f k ∗ f k ∗ f k = f k ∗ f k ∗ f k ③结合律 ( ) [ ( ) ( )] ( ) ( ) ( ) ( ) 1 2 3 1 2 1 3 f k ∗ f k + f k = f k ∗ f k + f k ∗ f k ②分配律 ④与单位样值函数的卷积和 由定义：∴ f (k)∗δ (k) = f (k) ( ) ( ) ( ) 1 1 f k ∗δ k − k = f k ( ) ( ) ( ) 1 2 1 2 f k − k ∗δ k − k = f k − k − k 求复合系统的 。 子系统的单位样值响应 分别为 例 已知复合系统由两个子 系统级联而成， , ( ) ( ), ( ) ( ) ( ) 1 : 2 1 h k b k h k h k a k k k ε ε = = h(k) ( ) h1 k ( ) h2 k f (k) y (k) f ( ) ( ) ( ) ( ) ( ) 0 1 2 h k h k h k a i b k i k i k i i = ∗ = ⋅ − − = 解： ∑ ε ε 1 ( ) 1 ( ) 1 b a k b a k b − − = + ( ) 1 1 k b a b a k k ε − − = + + i k i k i k k i i b a h(k) a (b) b ( ) 0 0 ∑ ∑= − = = = a ≠ b a = b ( ) (1) (1) ( 1) ( ) 0 0 h k b b k b k i k k i i k k i k = ∑ = ∑ = + ε = = a = b = 1 ε (k ) ∗ ε (k ) = (k + 1)ε (k )