《电路》课程教学资源（PPT课件）第4章 电路定理（Circuit Theorems）

第四章 电路定理

第四章 电 路 定 理

第4章 电路定理(Circuit Theorems) 4.1叠加定理(Superposition Theorem) 4.2替代定理(Substitution Theorem) 4.3戴维南定理和诺顿定理 (Thevenin-Norton Theorem 4.4特勒根定理(Tellegen's Theorem) 4.5互易定理(Reciprocity Theorem) 4.6对偶原理(Dual Principle)

第4章 电路定理 (Circuit Theorems) 4.1 叠加定理 (Superposition Theorem) 4. 2 替代定理 (Substitution Theorem) 4.3 戴维南定理和诺顿定理 (Thevenin-Norton Theorem) 4. 4 特勒根定理 (Tellegen’s Theorem) 4. 5 互易定理 (Reciprocity Theorem) 4. 6 对偶原理 (Dual Principle)

第4章电路定理 (Circuit Theorems) ◆重点： 1.熟练掌握叠加定理，替代定理，戴维南和诺顿定理。 掌握特勒根定理和互易定理； 2.了解对偶原理

 重点: 1. 熟练掌握叠加定理，替代定理，戴维南和诺顿定理。 掌握特勒根定理和互易定理； 2. 了解对偶原理。 第4章 电路定理 (Circuit Theorems)

4.1叠加定理(Superposition Theorem 如图电路，计算各支路电流。 用回豫)iR,山， 0R2 R3 -R2ia+R2+R3)b=儿s2 Us3. Ruia+Rizip-Usu Rzi+Rzis-Us22 R1=R1+R2,R12=-R2,儿s1n=儿s1儿s2 其中R1-R,R2RtR,M,2,4s3

4.1 叠加定理 (Superposition Theorem) 如图电路，计算各支路电流。 用回路法： (R1+R2 )ia-R2 ib =us1-us2 -R2 ia+(R2+R3 )ib =us2- us3 R11ia+R12ib =us11 R21ia+R22ib =us22 其中 R11=R1+R2 , R12= -R2 , us11=us1-us2 R21= -R2 , R22=R2+R3 , us22=us2-us3 R1 us1 R2 us2 R3 us3 i1 i2 i3 + – + – + – ia ib

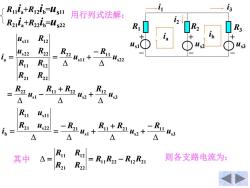
Ruig+Riip-Usu i3 用行列式法解 Rzig+Rzzip-Ws22 R3 Usti R2 i= Us22 Rz Ru R12 R2n+ △ △ Rz R22 R22 △ △ △ △ 其中△= Ru R=RR:2-Rn2Ra 则各支路电流为： R21R22

s 3 1 2 s 2 1 1 2 2 s1 2 2 s22 1 1 s1 1 2 2 2 1 2 2 1 1 1 2 s2 2 2 2 s1 1 1 2 a u R u R R u R u R u R R R R R u R u R i Δ Δ Δ Δ Δ + + = − − = = + s 3 1 1 s 2 1 1 2 1 s1 2 1 s2 2 2 1 1 1 s1 1 b u R u R R u R u R R u i Δ Δ Δ Δ − + + + − = = 其中 1 1 2 2 1 2 2 1 则各支路电流为： 2 1 2 2 1 1 1 2 R R R R R R R R Δ = = − R1 us1 R2 us2 R3 us3 i1 i2 i3 + – + – + – ia ib R11ia+R12ib =us11 R21ia+R22ib =us22 用行列式法解：

i=i= R2 ust △ △ +Rug=t △ 或=1-6={ tRu Ru+R+R R+R24g △ △ △ =方+2+ =元=尽1队1+Rt尼L十尼，=话+6+写 △ △ △ 由上式可见，各支路电流均为各电压源的一次函数，所以 各支路电流（如)均可看成各电压源单独作用时，产生 的电流（如，i”,”)之叠加

' '' ''' u i i i R u R R u R i i s 3 1 1 1 1 2 s 2 1 2 2 2 s 1 2 2 1 a + = + + + = = − Δ Δ Δ ' '' ''' i i i u R R u R R R R u R R i i i 2 2 2 s 3 1 1 1 2 s 2 1 1 1 2 2 2 s 1 2 1 2 2 2 a b 1 = + + + + + + + − + = − = Δ Δ Δ ' '' ''' u i i i R u R R u R i i s 3 3 3 3 11 s 2 11 21 s 1 21 3 b = + + − + + + − = = Δ Δ Δ 各支路电流（如i1）均可看成各电压源单独作用时，产生 的电流（如i1 ' ，i1 " ，i1 "'）之叠加。 由上式可见, 各支路电流均为各电压源的一次函数，所以

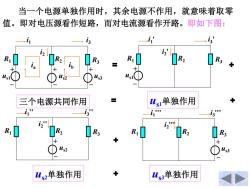
当一个电源单独作用时，其余电源不作用，就意味着取零 值。即对电压源看作短路，而对电流源看作开路。即如下图： 3 一3' R3 三个电源共同作用 Ws单独作用 3" R3 R 山、2单独作用 + 山s3单独作用

当一个电源单独作用时，其余电源不作用，就意味着取零 值。即对电压源看作短路，而对电流源看作开路。 三个电源共同作用 = = us1单独作用 + us2单独作用 + + us3单独作用 + 即如下图： R1 us1 R2 us2 R3 us3 i1 i2 i3 + – + – + – ia ib R1 us1 R2 R3 i1 ' i2 ' i3 ' + – R1 R2 us2 R3 i1 '' i2 '' i3 '' + – R1 R2 R3 us3 i1 ''' i2 ''' i3 ''' + –

i 举例证明定理 113 1a2 证明 i1=i11+i12+i13

举例证明定理 ib1 ia1 R1 R2 R3 + – us1 i11 ib ia R2 + – R3 + – R1 + – us1 us2 us3 i1 ib2 ia2 R2 + – R1 R3 us2 i12 ib3 ia3 R2 R3 + – R1 us3 i13 i1 = i11 + i12 + i 证明 13

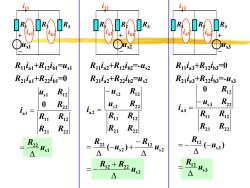
IOIROR b3 Ruiat+Rizipl=ust Ruia2+R12in2=-us2 R11a3+R12b3=0 Rziial+R22ipI=0 Rzia2+R22i2=us2 R21ia3+R22ib3=-us3 ust R12 -Us2 Ri2 0 R12 0 R22 us2 R22 in3 -Us3 R22 R12 R R12 R R2 R2 R22 R21 R22 R21 R22 R业1 △ (-,2)+ △ △ △ z+Riu? Ryus △ △

ib1 ia1 R1 R2 R3 + – us1 i11 ib2 ia2 R2 + – R1 R3 us2 i12 ib3 ia3 R2 R3 + – R1 us3 i13 R11ia1+R12ib1=us1 R21ia1+R22ib1=0 R11ia2+R12ib2=-us2 R21ia2+R22ib2=us2 R11ia3+R12ib3=0 R21ia3+R22ib3=-us3 Δ s1 22 21 22 11 12 22 s1 12 a1 0 u R R R R R R u R i = = Δ Δ Δ s s s2 12 22 s2 12 s2 22 21 22 11 12 2 22 2 12 a2 ( ) u R R u R u R R R R R u R u R i + = − − = − + − = Δ Δ s3 12 s3 12 21 22 11 12 s3 22 12 a3 ( ) 0 u R u R R R R R u R R i = = − − − =

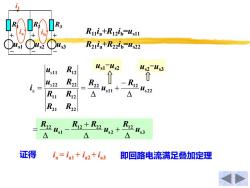
Ruia+Rizip-usu 3 Rzia+Rzip-us22 R12 us1-儿s2 us2 Us3 个 i= Us22 R22 Ru Ri2 △ △ R21 R22 △ R2+R2W,+ △ Rzus3 △ 证得 ia=ia+in2+ia3 即回路电流满足叠加定理

ib ia R2 + – R3 + – R1 + – us1 us2 us3 i1 R11ia+R12ib =us11 R21ia+R22ib =us22 Δ Δ s s a s2 2 1 2 s1 1 2 2 2 1 2 2 1 1 1 2 2 2 2 2 1 1 1 2 u R u R R R R R u R u R i − = = + s3 1 2 s2 1 2 2 2 s1 2 2 u R u R R u R Δ Δ Δ + + = − us1-us2 us2-us3 ia = ia1 + ia2 + i 证得 a3 即回路电流满足叠加定理