《电路》课程教学资源（PPT课件）第9章 正弦稳态电路的分析

第九章 正弦稳态电路的分析

第九章 正弦稳态电路的分析

第九章 正弦稳态电路的分析 §9-1阻抗和导纳 §9-2阻抗（导纳）的串联和并联 § 9一3电路的相量图 § 9一4正弦稳态电路的分析 § 9一5正弦稳态电路的功率 9一6功率因数的提高 §9-7最大功率传输 § 9一8串联电路的谐振 § 9一9并联谐振电路 2-2

第九章 正弦稳态电路的分析 2-2 § 9－1 阻抗和导纳 § 9－2 阻抗（导纳）的串联和并联 § 9－3 电路的相量图 § 9－4 正弦稳态电路的分析 § 9－5 正弦稳态电路的功率 § 9－6 功率因数的提高 § 9－7 最大功率传输 § 9－8 串联电路的谐振 § 9－9 并联谐振电路

§9一1阻抗和导纳 阻抗和导纳的概念以及对它们的运算和等效变换是线性电 路正弦稳态分析中的重要内容。 一.复数阻抗Z: 下图(a)所示为一个含线性电阻、电感和电容等元件， 但不含独立源的一端口N。 当它在角频率为ω的正弦电压（或正弦电流）激励下处于 稳定状态时，端口的电流（或电压）将是同频率的正弦量 应用相量法，端口的电压相量)与电流相量的比值定义为 该一端口的阻抗Z(又叫等效阻抗输入阻抗，驱动点阻抗)。 No 等效 图(a)

等效 Z U  I  I U Z   = § 9－1阻抗和导纳 阻抗和导纳的概念以及对它们的运算和等效变换是线性电 路正弦稳态分析中的重要内容。 一.复数阻抗 Z： 下图（a）所示为一个含线性电阻、电感和电容等元件， 但不含独立源的一端口N0。 当它在角频率为的正弦电压（或正弦电流）激励下处于 稳定状态时，端口的电流（或电压）将是同频率的正弦量。 I 应用相量法 U   ,端口的电压相量 与电流相量 的比值定义为 该一端口的阻抗 Z(又叫等效阻抗,输入阻抗,驱动点阻抗)。 I  U N0  图（a）

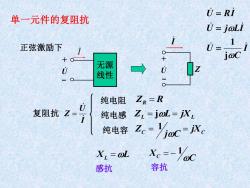
U-RI 单一元件的复阻抗 U=joLi 正弦激励下 0= 1 jwC 无源 线性 纯电阻 ZR=R 复阻抗Z= 纯电感 Z=joL=iX 纯电容 Ze-Yjoc=Xc X:.=@L X=-%c 感抗 容抗

C XC  = − 1 单一元件的复阻抗 正弦激励下 I  U  Z + - 无源 线性 I  U  + - I U Z   复阻抗 = 纯电阻 ZR = R L L 纯电感 Z = jL = jX C C jX j C Z = =  纯电容 1 XL =L 感抗 容抗 I C U U j LI U RI         j 1 = = =

(1)Z和总电流、总电压的关系 由复数形式的欧姆定律心=☑ 可得： U 84k。片Q-只是 Z=140. 电阻 电抗 阻抗模： 阻抗角： P2=p-0 结论：Z的模为电路总电压和总电流有效值之比， 而Z的幅角则为总电压和总电流的相位差。 阻抗适合于串联电路的计算，单位是欧姆

由复数形式的欧姆定律 U  = I  Z 可得： 结论：Ｚ的模为电路总电压和总电流有效值之比， 而Ｚ的幅角则为总电压和总电流的相位差。 （１）Z 和总电流、总电压的关系 I U 阻抗模: Z = Z =u −i 阻抗角: R j X I U Z I U I U Z Z u i i u =  =  − = +   = =        电阻 电抗 阻抗适合于串联电路的计算,单位是 欧姆

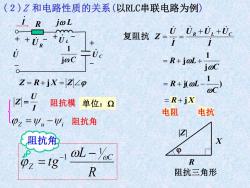
(2)Z和电路性质的关系（以RLC串联电路为例） I.R joL 0 复阻抗Z=7 0R+0.+0c ++UR +UL U jwC 1 =R+j@L+ jwC Z=R+jX=|Z∠p =R+j(@L 阻抗模单位：2 =R+jX 电阻 电抗 p2=-必，阻抗角 ☑ 阻抗角 X ol-Yoc Pz=ig R R 阻抗三角形

电阻 电抗 . I R j L + - + - + - . U U L . U C . jωC 1 + - UR  I U U U I U Z R L C       + + 复阻抗 = = C R L   j 1 = + j + ) 1 j( C R L  = +  − = R + jX |Z| R X  阻抗三角形 Z = u − i 单位： I U Z = 阻抗模 阻抗角 Z = R+ jX = Z  (２)Z 和电路性质的关系(以RLC串联电路为例) R L t g C Z    1 1 − = − 阻抗角

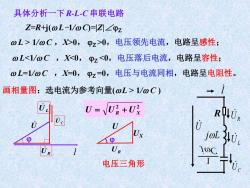
具体分析一下R-L-C串联电路 Z=R+j(oL-1/oC-Z☑∠0z oL>1/oC,0,pz>0,电压领先电流，电路呈感性： oL1/oC) U-JUR+Ux RUR joL UR 电压三角形

具体分析一下R-L-C 串联电路 Z=R+j( L-1/ C)=|Z|∠Z  L > 1/ C ，X>0， Z >0，电压领先电流，电路呈感性；  L 1/ C ) UC  I  UR  UL  U   2 2 U = UR + U X 电压三角形 UX UR U   L=1/ C ，X=0， Z =0，电压与电流同相，电路呈电阻性。 R UR  UL  UC  I  U  jL jC 1

ROUR 假设R、L、C已定， 电路性质能否确定？ joL 0 (阻性？感性？容性？ 不能！ XL=0L、XC= @C 当w不同时，可能出现： X>Xc,或X<Xc,或X-Xc。 2-81

假设R、L、C已定， 电路性质能否确定？ （阻性？感性？容性？） 不能！ 当ω不同时，可能出现： XL > XC ，或 XL < XC , 或 XL =XC 。 C XL L XC   1 = 、 =  2-81 R UR  UL  UC  I  U  jL jC 1

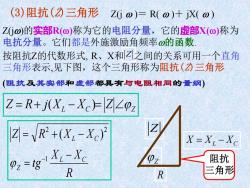
(3)阻抗()三角形 Z(Gw)=R(0)+jX(0) Z(jo)的实部R(@)称为它的电阻分量，它的虚部X(O)称为 电抗分量。它们都是外施激励角频率⊙的函数 按阻抗Z的代数形式，R、X和Z之间的关系可用一个直角 三角形表示，见下图，这个三角形称为阻抗()三角形 (阻抗及其实部和虚部都具有与电阻相同的量纲) Z=R+jX-Xc上|Z∠pz Z=R2+(X-Xc) X=XI-XC 0,=g- 阻抗 R R 三角形

(3)阻抗(Z)三角形 阻抗 三角形 Z Z R X = XL − XC R X X t g Z R X X L C Z L C − = = + − −1 2 2 ( )  XL XC Z Z Z = R+ j( − )=  Z(j  )＝ R(  )＋ jX(  ) Z(j)的实部R()称为它的电阻分量，它的虚部X()称为 电抗分量。它们都是外施激励角频率的函数. 按阻抗Z的代数形式, R、X和 Z 之间的关系可用一个直角 三角形表示,见下图，这个三角形称为阻抗(Z)三角形 (阻抗及其实部和虚部都具有与电阻相同的量纲)

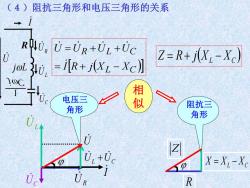
(4)阻抗三角形和电压三角形的关系 ROLU U=UR+UL+UC Z=R+j(Xi-Xc) =[R+XL-Xc〗 电压三 似 角形 阻抗三 角形 X=XL-Xc R

（４）阻抗三角形和电压三角形的关系 电压三 角形 阻抗三 角形 相 似  ( C ) L R L C I R j X X U U U U = + − = + +      ( ) XL XC Z = R + j −  Z R X XL XC = − UC   UR  U  UL  UL UC   + I  R UR  UL  UC  I  U  jL jC 1