《信号与系统》课程授课教案（课件讲稿）第4章 连续系统的频域分析

第四章连续系统的频域分析Ci2 = 84-1信号分解为正交函数V.正交函数和正交函数集KB当，，完全重合，则=0,c2=11.正交矢量V.Ci2 V.随着夹角 8 增大，C12 威小;cos 0VV.当0=90,Ci2=0，和相互垂直C12=|cos 0 商网a.平面，x、y正交坐标系c. 般:Vy-0, itj令x方向正交单位失量LV=k矢量：令，y方向正交单位矢量A-C+Cy+.+CY.A=CV,+Cy,C.为A在V.中的投影b.三维，x、y、z正交坐标系C,=A正交量集,,)A=CV,+CV, +CV.3.正交函数集2. 正交函数①正交函数集定义：在(1,)区间内，若函数()和p,(1)定义：若n个函数(),,(1)，,(0)满足构成一个函数集,且在区间（t,t)内满足T"0.(0)g:(0)t = 0r0ij"o(t)0;(t)dt =3Lk,0 i=j则称 g,(t)和 pz()在区间 (ti,t,)内正交称此函数集是(t1,t2)区间上一组正交函数集

1 第四章 连续系统的频域分析 §4-1 信号分解为正交函数 一.正交函数和正交函数集 1.正交矢量 C12 V2 V1 cos θ G G = 2 1 2 2 2 1 cos V V V V V V G G G G G G ⋅ = = θ θ → C12 V2 → V1 → V2 2 2 1 2 12 V V V C K G G ⋅ = 当 ， 完全重合，则 随着夹角θ增大， 减小； 当 ， 和 相互垂直 V1 G V2 G 0, 1 θ = c12 = 12 c 90 , 0 = c12 = o θ V1 G V2 G A C1vx C2vy G G = + A C x C y C z v v v 1 2 3 G G G = + + a. 平面, x、y正交坐标系 令 vx : x方向正交单位矢量 G 令 v y : y方向正交单位矢量 G b. 三维, x、y、z正交坐标系 {v ,v ,v } x y z G G G 正交矢量集 0, i j Vi ⋅Vj = ≠ G G i i i V ⋅V =k G G c. 一般: A CV CV Cn Vn G " G G 矢量: = 1 1 + 2 2 + + Cm为A在Vm中的投影 G 2 m m m V A V C G G ⋅ = 2. 正交函数 ( ) ( ) 0 2 1 1 2 = ∫ t t dt t t ϕ ϕ ( ) ( ) (t , t ) . 则称 ϕ 1 t 和ϕ 2 t 在区间 1 2 内正交 ( , ) ( ) ( ) 1 2 1 2 定义：在 t t 区间内，若函数ϕ t 和ϕ t 满足 3. 正交函数集 = ∫ t t dt t t j 2 1 ( ) ( ) ϕi ϕ k i j i j i ≠ = ≠ 0 0 . ( , ) 1 2 函数集 称此函数集是 t t 区间上一组正交 ( ) ( ) ( ) 1 2 n t t t 定义：若 个函数ϕ ，ϕ ，"，ϕn 构成一个函数集,且在区间（t 1,t2 )内满足 ①正交函数集

②完备的正交函数集③信号分解为正交函数如果(9,(1),,(t),,甲,(t)是一组正交函数集,f(t)在(t,t,)有定义,f(t)可近似表示为且对任意v(t)m(t),m=1,2, ,n,不存在F()C()+c9()++c,,(t)-Zc,(t)'v(0).()dt=0 (m=1,, n)均方误差称此函数集为完备正交函数集.(-e0(0d2=t -t, Ja?令=0J'y'(t) d :ckac.i=禁务's(0)g,(0)dtk,=I'ojdt得cj ='o;(t)dt此时()=Ci()+c9(t)++c,甲,(t)+..4.常用正交函数集若n→,=0,得①三角函数集(cos no,t,sinno,t) n=0,±1,+2..②复指数函数集$4-2付立叶级数与周期信号的频谱(eina")n = 0,±1,±2....周期信号r(t)满足Dirichlet条件时，在区间（to,t+T)可以展开成在完备正交信号③勒让德多项式空间中的无穷级数。如果完备的正交函④切比雪夫多项式数集是三角函数集或指数函数集，那么，周期信号所展开的无穷级数，就分③沃尔什函数别称为“三角形付立叶级数"或“指数形式付立叶级数，统称为付立叶级数

2 ②完备的正交函数集 { ( ), ( ), , ( )} , 如果 ϕ 1 t ϕ 2 t " ϕ n t 是一组正交函数集 ( ) ( ) 0 ( 1,2, , ) 2 1 t t dt m n t t ∫ ψ ϕ m = = " 称此函数集为完备正交 函数集. 且对任意 ψ(t) ≠ϕ m(t),m = 1,2,",n, 不存在 ∑= ≈ + + + = n j n n j j f t c t c t c t c t 1 1 1 2 2 ( ) ϕ ( ) ϕ ( ) " ϕ ( ) ϕ ( ) ③信号分解为正交函数 f (t)在(t1 , t2 )有定义 , f (t)可近似表示为 f t c t dt t t n j j j t t 2 1 2 1 2 [ ( ) ( )] 1 2 ∫1 ∑= − − ε = ϕ 均方误差 0 2 = ∂ ∂ j c ε 令 ∫ ∫ = 2 1 2 1 ( ) ( ) ( ) 2 t t j t t j j t dt f t t dt c ϕ ϕ 得 若 n → ∞,ε2 = 0, 得 k dt t t j = ∫ j 2 1 2 ϕ ∫ ∑ ∞ = = 1 2 2 2 1 ( ) j j j t t f t dt c k 帕斯瓦 尔方程 此时 f (t) = c1 ϕ1 (t) + c2ϕ 2 (t) +"+ cnϕ n (t) +" 4. 常用正交函数集 {cos nω1t,sin nω1t} n = 0,±1,±2" ①三角函数集 {e jnω1t } n = 0,±1,±2" ②复指数函数集 ③勒让德多项式 ④切比雪夫多项式 ⑤沃尔什函数 §4-2付立叶级数与周期信号的频谱 周期信号f(t)满足Dirichlet条件时，在 区间（t0,t0+T)可以展开成在完备正交信号 空间中的无穷级数。如果完备的正交函 数集是三角函数集或指数函数集，那 么，周期信号所展开的无穷级数，就分 别称为“三角形付立叶级数”或“指数形式 付立叶级数”，统称为付立叶级数

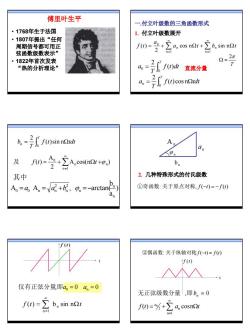
傅里叶生平一.付立叶级数的三角函数形式·1768年生于法国1.付立叶级数展开·1807年提出“任何(0)=%+a. cos nQt+Zb. sin nQt运周期信号都可用正弦函数级数表示”Q=2元·1822年首次发表α=号 ()dl 直流分量“热的分析理论”f" f(t)cos nQtdta.=TJ2rT f(t)sin nQtdtb.:AT.a.o.(0=+2A.cos(n21+9.)及b.n=2.几种特殊形式的付氏级数其中A= A=+,=arctan①奇函数：关于原点对称,f(-1)=-f(0)a.if(t)②偶函数:关于纵轴对称(-1)=f(0)f(t)仅有正弦分量即a=0 a.=0无正弦级数分量,即b,=0f(t)=-Z b, sin nQ21(0)=%+2 a. cosn21n=l

3 傅里叶生平 • 1768年生于法国 • 1807年提出“任何 周期信号都可用正 弦函数级数表示” • 1822年首次发表 “热的分析理论” 一.付立叶级数的三角函数形式 1. 付立叶级数展开 T 2π Ω = ∑ ∑ ∞ = ∞ = = + Ω + Ω n 1 1 n n n 0 cos n sin n 2 ( ) a t b t a f t = ∫ 直流分量 T f t dt T a 0 0 ( ) 2 = ∫ Ω T f t tdt T a 0 n ( ) cos n 2 = ∫ Ω T f t tdt T b 0 n ( )sin n 2 A cos(n ) 2 A ( ) n n 1 n 0 = +∑ Ω +ϕ ∞ = 及 f t t 其中 ) a b A A , arctan( n n n 2 n 2 0 = a0 n = an +b ϕ = − A n bn n a ϕ n ①奇函数:关于原点对称, f (−t) = − f (t) 2. 几种特殊形式的付氏级数 仅有正弦分量,即a0 = 0 an = 0 f t = ∑ Ωt ∞ = ( ) b sin n n 1 n t f (t ) f t a t a = +∑ Ω ∞ = ( ) cosn n 1 2 n 0 t f (t) ②偶函数: 关于纵轴对称, f (−t) = f (t) 无正弦级数分量 ,即bn = 0

④偶谐波函数③奇谐波函数 f(t+)=-f(t)(t)f(t)只有奇次谐波1- af(t)=Z A2n-COS(2n-1)2t+ @2m-1 2n=lk = 1,2,3,4 3、信号的分解二、付立叶级数的指数（复数）形式奇函数部分偶函数部分由欧拉公式2f(t)= foa(t)+ fa(t)Sin nQt = e/ml-e'm2jf(-t)=-foa(t)+ fe(t): 1.(0)-10--0.()-10+- emai + e-/na!cos nQt =222b.,+ ja,em +e-moyF.:(a, +jb.)f(0)=%+Zar2jC6-9令+2b.(e/nare-jn2t)122Ddf(0)=F +2F,ern jn2F.e=+2(=ihena ++ibhem)n=122l2ZF.ero二Fa=2(a.-Jb)=1A.eno=-0

4 ) ( ) 2 ( f t T ③奇谐波函数 f t ± = − f(t) t ( ) A COS[(2n 1) ] 2n 1 n 1 2n 1 − ∞ = f t =∑ − − Ωt +ϕ k = 1 ,2 ,3 ,4 " 只有奇次谐波 f (t) t ④偶谐波函数 A Cos(2n ) 2 A ( ) 2n n 1 2n 0 = +∑ Ω +ϕ ∞ = f t t f (t) f (t) f (t) = od + ev 奇函数部分 偶函数部分 f ( t) f (t) f (t) − = − od + ev 3、信号的分解 2 ( ) ( ) ( ) 2 ( ) ( ) ( ) f t f t f t f t f t f t od ev + − = − − ∴ = j e e t j t j t 2 sin n nΩ − nΩ − Ω = 2 cos n jn t jn t e e t Ω − Ω + Ω = 二. 付立叶级数的指数(复数)形式 由欧拉公式 2 2 ( ) n n n 1 n 0 j t j t e e a a f t ∞ Ω − Ω = + = +∑ ∑ ∞ = Ω + − Ω + − = + n 1 0 n n n n n n ) 2 2 ( 2 j t j t e a jb e a a jb ( ) 2 1 n n n 1 n j t j t e e j b Ω − Ω ∞ = +∑ − n j n n n n A e 2 1 ( ) 2 1 ϕ 定义 F = a − jb = ( ) 2 1 2 n n n n n a jb j b ja F = + + = − − − 2 0 0 a 令 F = j t j t f t F F e F e− Ω ∞ = − Ω ∞ = = +∑ +∑ n n 1 n n n 1 0 n ( ) j t F e Ω ∞ = −∞ = ∑ n n n

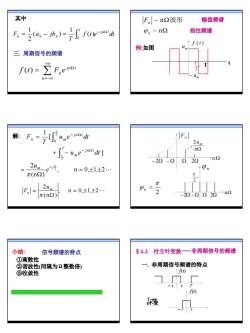
其中IF.l～nQ波形幅值频谱P,~n相位频谱e-manaF,=(a.- jb.)=uL/(0)例：如图三.周期信号的频谱ZF,en!f(t)=n=-0解 F,=,ume-mard↑[F. ]Ume-jno'dt ]nd-20-Q2202ume-号Pnn = 0,±1,±2....元(n2)0.号2umF,/ =n = 0,±1,±2...-20-2220n2元(n2)]付立叶变换一非周期信号的频谱小结：$4-3信号频谱的特点①离散性一，非周期信号频谱的特点②谐波性(间隔为 α整数倍)1f0)③收敛性中-tt10)曼.中

5 f t e dt T F a jb j t T − Ω ∫ = − = n 0 n n n ( ) 1 ( ) 2 1 其中 ∑ +∞ = −∞ Ω = n n n ( ) j t f t F e 三. 周期信号的频谱 Fn ~ nΩ波形 幅值频谱 ϕ n ~ nΩ 相位频谱 T 2 T t − um m u f ( t ) 例:如图 ] 2 n u e dt T j t ∫T m − Ω + − u e dt T F T j t ∫ m − Ω = 2 0 n n [ 1 解: , n 0, 1, 2" (n ) 2 2 = ± ± Ω = − π π m j e u , n 0, 1, 2" (n ) 2 n = ± ± Ω = π m u F − 2Ω − Ω Ω 2Ω Fn πΩ m 2u n Ω 2 n π ϕ = −2Ω −Ω Ω 2Ω ϕ n 2 π nΩ 信号频谱的特点 ①离散性 ②谐波性(间隔为Ω整数倍) ③收敛性 小结: §4-3 付立叶变换 非周期信号的频谱 f(t) −τ τ T f(t) −τ τ T→∞ τ不变 一. 非周期信号频谱的特点

F.l1. 引例2P=2+f(0)F, = I sin angr吉-2npETT-ET+E2TnoQr[F.p=！1 sinP = 4SFr=PFNn23号-2 -11②.频谱特点|Fn|→0谱成连续T→8P→82.频谱特性JinF,=0有界函数①连续性与离散性=lin F,T定义 F(o)=linAα=(n+1)Q-nQ=Q= 记为doT→8 40→0频谱密度数简称频谱函娄n→又:F=1y y(be-maratF(a)=limTF(no). F(Go)=//mTF. =["()-1ardtlimJ f(0)e-mn dt二、 付立叶变换与反变换1.付立叶变换1(0)e8 dT-00-00F(jo)- f(t)e-jar dt付立叶变换

6 f(t) 2 2 T τ τ − 2 2 τ τ T − T + 2 n 2 n n sin ω τ ω τ τ Ω Ω = T F 1. 引例 ) n ( 1 sin 1 n n p S P P F T p a P P k π τ π π 令 = = ⋅ = − 2 − 1 1 2 2 1 Fn P n P = 2 Fn −2 −1 1 2 3 P n P = 4 4 1 P 0 T → ∞ → ∞ Fn → 谱成连续 T 2 (n 1) - n π ∆ω = + Ω Ω = Ω = 2. 频谱特性 ①连续性与离散性 T → ∞ ∆ω → 0 记为dω nΩ → ω ②. 频谱特点 ∵ linFn = 0 T →∞ 定义 F T T F F j lin lin T T n n 1 ( ) → ∞ → ∞ ω = = 有界函数 频谱密度函数 简称频谱函数 ( ) ( ) 1 lim 1 1 T F ω TF nω →∞ = 1 1 1 1 j 2 2 ( )e d lim T n t T T f t t − ω − →∞ = ∫ ω 1 −j nω ( ) t →∞ f t e dt T1 ∞ − ∞ 2 T1 2 T1 − f ( )t e dt T F j t T T − Ω ∫− = n n 2 2 1 又 ∵ F ( ) () j li TF f t e dt jωt ω − ∞ ∫− ∞ ∴ = m n = T → ∞ F ( ) () j f t e dt jωt ω − ∞ ∫−∞ = 二. 付立叶变换与反变换 1. 付立叶变换 付立叶变换

一般3.F与Fjo)的比较及物理意义F(j@)= A(0)+ jB(0)= [F(io)ej0(o)网10)-ZF,e/morF,=y(0e-mardt[Fjo]:幅值频谱非周期信号相位额谱p(o):0-rbodo Fio)-Lr(0e-a2．付立叶反变换0FU0)-10m7FF,-F(jo)o-n知 F(jo)→r(l)F；频带离散.收敛1-F(dF(jo)：频谱连续，但不一定收敛三典型信号的付立叶变换(频谱）2. 单边指数信号 e-"u(t),α>01. 冲激函数 8(t)F(jo)- It" e-ae-jou(t)dtF(jo)- fts(t)e-ia dt = e-i0 =11-fre(atiol dt=ir()[Flia]α+jat()3.双边指数信号tf(t)=e-all, α >08()1F(jo)- J'e"e-iardt + J.I" e-at e- jot dtVosFF(io)= [[, Ee-iot dt2α-jo-a'+0()(d)Eteioi-ja24.矩形脉冲信号Et2joTE-Ers()-/20/2

7 F( ) jω = A(ω) () + jB ω ( ) ϕ ( ) ω ω j = F j e 一般 F( jω) : 幅值频谱 ϕ( ) ω : 相位频谱 2. 付立叶反变换 ( ) ( ) ω ω π ω f t F j e d j t ∫ +∞ − ∞ = 2 1 知 F( ) jω → f (t) 非周期信号 3. F n 与F( ) jω 的比较及物理意义 ( ) ∑ ∞ =−∞ Ω = n n n j t f t F e ( ) ( ) ω ω π ω f t F j e d j t ∫ ∞ −∞ = 2 1 f ( )t e dt T F T T j t ∫− − Ω = 2 2 n n 1 F( ) () j f t e dt j t ∫ ∞ −∞ − = ω ω ( ) n = = nΩ 1 ω ω F j T F( jω) =limTFn F T →∞ F (jω ): 频谱连续 , 但不一定收敛 Fn : 频带离散. 收敛 周 期 非 周 期 关 系 三. 典型信号的付立叶变换(频谱) 1. 冲激函数δ (t) ( ) () 1 0 = = = − +∞ −∞ − ∫ j t j F j t e dt e ω ω δ (1) t f ( )t F( ) jω 1 ω δ ( )t ↔ 1 2. ( ), > 0 − α α e u t 单边指数信号 t F ( ) () j e e u t dt t j t ∫ +∞ − ∞ − − = α ω ω ( ) α ω α ω j e dt j t + = = ∫ +∞ − + 1 0 3. 双边指数信号 ( ) = , > 0 − α α t f t e ( ) ∫ ∫ ∞ − − − ∞ − = + 0 0 F j e e dt e e dt αt jωt αt jωt ω 2 2 2 α ω α + = 4. 矩形脉冲信号 E O f ( )t t −τ 2 τ 2 ( ) ∫− − = 2 2 j e d τ τ ω F jω E t t 2 2 j e j τ τ ω ω − − − = E t 2 j e e . 2 2 j 2 j τ ω τ ω τ ω τ − − = E 2 2 sin ωτ ωτ τ       = E       = 2 Sa ωτ Eτ

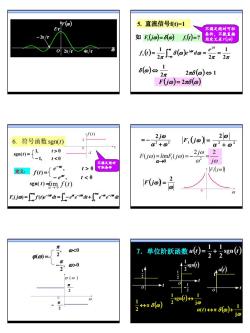
tr(a)5. 直流信号(t)=1Et满足绝对可积不能直如 F(io)=8(a)(0)-?2元/t1.0.02元/4元/ s(o)eian do =.(0)=-2元2元6(0)≤ 2元2元8()α1F(j0)=2元(0)f(1)2jo20F(jo)6.符号函数sgn(t)α+0α+?Ot>0sgn(t)= /1,2j02F(jo)=limF(jo)=-[-1.10[F(Go )e定义：F()=t0)10(0)元-200gn(d)0jo元 S(0)u(t) n (0)+io

8 ω F(ω) Eτ O 2π τ 4π τ − 2π τ ( ) ( ) π π δ ω ω π ω 2 1 2 2 1 0 1 = = = ∫ ∞ −∞ j j t e f t e d 5. 直流信号f(t)=1 如 F1(jω) = δ (ω) () f1 t = ? F(jω) () = 2πδ ω ( ) 2 1 π δ ω ⇔ 2πδ ( ) ω ⇔ 1 不满足绝对可积 条件，不能直接 用定义求F(jω) 6. 符号函数 sgn(t) sgn(t) = 1, 0 1, 0 − t t sgn( t) =lim f (t) α → 0 t 1 -1 0 f (t) f (t) = , 0 , 0 − − e t e t t t α α 定义： F j f t e dt e e dt e e dt jωt αt jωt αt jωt ω − +∞ − − −∞ − +∞ ∫−∞ ∫ ∫ = = − + 0 0 1( ) ( ) 不满足绝对 可积条件 2 2 2 α ω ω + = − j ( ) 1 2 2 2 α ω ω ω + F j = ( ) ω ω 2 F j = F1 ( ) jω 0 ω ω ω ω ω ω j j F j li F j 2 2 ( ) m ( ) 1 2 = = − = α→0 ϕ(ω) = , 0 2 , 0 2 − > < ω π ω π ϕ (ω ) 0 2 π 2 π − ω π δ ( ) ω 2 1 ↔ ( ) jω 1 sgn 2 1 t ↔ 7．单位阶跃函数 u( )t sgn ( )t 2 1 2 1 = + O t 2 1 O t 2 1 2 1 − sgn( )t 2 1 ( ) ω δ ω j 1 u(t) ↔π + O t 1 u(t)

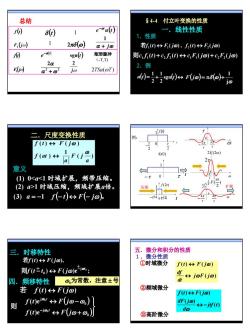
总结$4-4付立叶变换的性质线性性质e-"u(0)r0)(0)11.性质112元8(a)F,(Gio)α+ ja若fi(t)台F(jの), f,(t)台F(jo)e-all心sgn(0)矩形脉冲 则cJ(t)+c, J(t)c,F(jo)+c,F,(jo)(-T,T)2α2.例F(ia)2TSa(oT)joα'+an()=1+!-+()+ FUo)-n8(o)170)尺度变换性质例：f(t)台 F(jo)T0F(20a)F0f(t/2)意义(1) 01 时域压缩，频域扩展a倍。压缩(3) a=-1 f(-t)αF(-jo)。-t/40T/4五。微分和积分的性质三.时移特性1.微分性质若f(t)台F(jの)①时域微分f(t) F(jw)则f(tt)F(jo)e joF(jo)の为常数，注意士号t四．频移特性②频域微分若f(t)αF(j)f(t)AF(jo)f(t)ejat αF(jo-o,)dF(j@)-jt(t)则dof(t)e-ia F(io+o,)③高阶微分

9 2 2 2 α ω α α + − t ( ) e F( ) jω f t 1 δ ( )t ( ) jω t 2 sgn ( ) α ω α j e u t t + − 1 2TSa(ωT) 2πδ ( ) ω 矩形脉冲 （-T,T) 1 1 ( ) F ( ) jω f t 1 总结 ( ) () ω ω δ ω j 1 F j = π + 一．线性性质 1．性质 2．例 ( ) ( ) , ( ) ( ) 若f1 t ↔ F1 jω f2 t ↔ F2 jω ( ) ( ) ( ) ( ) 则c1 f1 t + c2 f2 t ↔ c1F1 jω + c2F2 jω u(t) = + sgn( )t ↔ 2 1 2 1 §4-4 付立叶变换的性质 二．尺度变换性质 意义 (1) 01 时域压缩，频域扩展a倍。 (3) a = −1 f () ( ) − t ↔ F − jω 。 ( ) 1 ( ) ( ) ( ) a F j a f at f t F j ω ω ↔ ↔ 0 t 2τ −τ τ τ π τ π− 0 ω 1 f (2t) −τ/4 0τ/4 t ) 2 ( 2 1 ω F 2 τ τ 4π τ 4π − 压缩 1 扩展 ω 0 例： f(t/2) 2F(2ω) f (t) 2 τ t 0 2 τ − 1 τ τ 2π τ 2π − 0 ω 若f (t) ↔ F( jω), 三．时移特性 若 f (t) ↔ F( jω) ( ) ( )e ( ) ( )e 0 j 0 j 0 0     ↔ + ↔ − − ω ω ω ω ω ω f t F j f t F j t t 则 四．频移特性 ω0为常数，注意 ± 号 ( ) ( )e ;0 j 0 t f t t F j ω ω ↔ − 则 − + + ( ) ( ) ( ) ω ω ω j F j dt df f t F j ↔ ↔ ( ) ( ) ( ) ( ) jtf t d dF j f t F j ↔ − ↔ ω ω ω 五．微分和积分的性质 １．微分性质 ①时域微分 ③高阶微分 ②频域微分

f)(io)F(jo)S分析drn"F(a)(-t (t)do"求导方波三角形函数例：求三角函数的频谱密度函数troE()求手→冲激函数方波一号2．积分特性0-+0)+司茶·若F[f(t)}= F(jo)j0% _4E+2E.-i0%FU"(0)]=2EF0O)=0-(io) F(jo)--0"F(j0)[2E0%_4E+2E0%F(jo)=0(oe]-F0a02joTESOT-2[2 sin )22.若例1.求单位阶跃画数的傅里叶变换。FIf(t)I= F(jの)解：已知u(n)-L_6(t)dt8(t)F(j0)±0则u(t)j0n 8(0)-1=+n8(0imG-fn例2.求门面数G,()职分的频谱函数。则*0.0 ()id三040由rSa(0)-，知F(0)+0[LG()at]-n (0)+()

10 ( ) jω F ( jω ) dt d f n n n ↔ ( ) ( ) ( ) jt f t d d F j n n n ↔ − ω ω 例：求三角函数的频谱密度函数． o f ( )t t 2 τ − 2 τ E 三角形函数 求导 → 方波 o f ′( )t t 2 τ − 2 τ τ 2E o f (t) t 2 τ − 2 τ E o f ′′( )t t 2 τ − 2 τ       τ 2E       τ 2E       τ 4E 方波 冲激函数 求导  → 分析 () () () ω F jω ω F jω 2 2 = j = − ( )       − + − = − 2 j 2 j 2 e 4 2 e 1 2 ωτ ωτ ω τ τ τ ω E E E F j 2 2 4 2 jsin 2      −  = ω τ τω E 2 4 Sa 2       = τE ω τ 2 j 2 j e 4 2 e 2 [ "( )] ωτ ωτ τ τ τ − = − + E E E F f t X ( )        − + −      = + 2 4 2 2 2 "( ) τ δ τ δ τ τ δ τ t E t E t E f t 2．积分特性 • 若 F[ f (t)] = F ( jω) F(j0)=0 ω ω τ τ j F j F f d t ( ) ( ) =      ∫−∞ 则 • 若 F( j0) ≠ 0 F[ f (t)] = F ( jω) ( 0) ( ) ( ) ( ) π δ ω ω ω τ τ F j j F F f d t = +       ∫−∞ 则 例1. 求单位阶跃函数的傅里叶变换。 ∫−∞ = t 已知 u(t) δ (t)d t δ (t) ↔ 1 π ( ) j 1 π ( ) 1 j 1 ( ) δ ω ω δ ω ω 则u t ↔ + ⋅ = +       ↔ 2 ( ) Sa ωτ τ τ G t 由τ Sa(0) = τ，知F( ) 0 ≠ 0 () ( )       = +     ∫−∞ 2 Sa j d π ωτ ω τ τ τ τ τδ ω t F G 例2.求门函数Gτ ( )t 积分的频谱函数。 t G (t) τ O 2 τ − 2 τ 1 解： 解： t ( ) 1 G t − τ τ O 2 τ − 2 τ