《机械测试技术基础》课程教学资源（作业习题）测试与检测技术基础习题集（清华大学，无答案）

《测试与检测技术基础》 习题集 王伯雄王雪李玉和罗秀芝选编 清华大学精密仪器与机械学系 2006年1月

《测试与检测技术基础》 习题集 王伯雄 王 雪 李玉和 罗秀芝 选编 清华大学精密仪器与机械学系 2006 年 1 月

绪言 本习题集适用于机械工程学院平台课《测试与检测 技术基础》，所采用的教材为《测试技术基础》。习题 选编时主要考虑加强学生对课程基本内容的理解，对学 生分析问题能力及应用能力的培养。习题集习题部分选 自已有的习题，部分是我们在科研工作中总结抽选出来 的成果内容。本习题集是原习题集2001版的再版，再 版时根据教学大纲对原内容进行了大幅度的修改，增加 了40%的习题量。 由于编者的水平和视野的局限性，在本题集的选材 和内容安排上一定有许多不足之处，恳望读者提出宝贵 意见。 2我年1月 1

·1· 绪言 本习题集适用于机械工程学院平台课《测试与检测 技术基础》，所采用的教材为《测试技术基础》。习题 选编时主要考虑加强学生对课程基本内容的理解，对学 生分析问题能力及应用能力的培养。习题集习题部分选 自已有的习题，部分是我们在科研工作中总结抽选出来 的成果内容。本习题集是原习题集 2001 版的再版，再 版时根据教学大纲对原内容进行了大幅度的修改，增加 了 40％的习题量。 由于编者的水平和视野的局限性，在本题集的选材 和内容安排上一定有许多不足之处，恳望读者提出宝贵 意见。 编者 2006 年 1 月

第1章绪论 1.什么是测量？试用数学关系式表达一个测量过程。 2.实施测量的基木前提条件是什么？ 3.什么是国际单位制？其基本量及其单位是什么？ 4.试述一个测试系统的基本组成及其各环节的功能。 5.考虑 根玻璃水银温度计作 一个测温系统，详细讨论组成该系统的各级 选 有关测试技术的参考书，写一篇关于其中一章测量某某物理量的过 程和方法的总结

·2· 第 1 章 绪 论 1．什么是测量？试用数学关系式表达一个测量过程。 2．实施测量的基本前提条件是什么？ 3．什么是国际单位制？其基本量及其单位是什么？ 4．试述一个测试系统的基本组成及其各环节的功能。 5．考虑一根玻璃水银温度计作为一个测温系统，详细讨论组成该系统的各级。 6．自己选择一本有关测试技术的参考书，写一篇关于其中一章测量某某物理量的过 程和方法的总结

第2章测试信号分析与处理 1,判断下列序列是否是周期函数。如果是，确定其周期。 ①回=e作 (2)xn）=ew210 2.已知周期信号x)的傅里叶系数是a,b,c。试证明延时信号x-o)的傅里叶级 数是 -小a+o.co.+6'sna） -Sc.em 其中：an=a cosn0k-b sinno b =a sinnooto+b cosnoolo Cn =Cne-moot 3。求周期信号的傅里叶级数，并绘出其频谱图 周期性锯齿波 x(t)=2/T.t t(-T2≤t≥T2) 周期方波 tx0= -A (-T/2sts0) A(0≤t≤T2) 全波整流 x(t)=ASin t

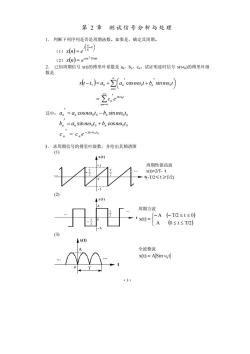
·3· 第 2 章 测试信号分析与处理 1． 判断下列序列是否是周期函数。如果是，确定其周期。 （1） ( ) ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = π 8 n j x n e （2） ( ) n x n ecos 10π 2 = 2． 已知周期信号 x(t)的傅里叶系数是 an，bn，cn。试证明延时信号 x(t-t0)的傅里叶级 数是 ( ) ∑ ∑ +∞ =−∞ ∞ = ′ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ′ + ′ − = + n jn t n n n n c e x t t a a n t b n t 0 0 1 0 0 0 cos sin ω ω ω 其中： 0 0 0 0 a a cosn t b sin n t n = n ω − n ω ′ 0 0 0 0 b a sin n t b cosn t n = n ω + n ω ′ 0 0 jn t n n c c e − ω = ′ 3． 求周期信号的傅里叶级数，并绘出其频谱图 (1) x(t) t 2 T − 0 + 1 -1 . 2 T . (2) x(t) t 2 T − 0 A - A . 2 T . (3) x(t) t 0 A . . T 周期性锯齿波 x(t)=2/T• t (-T/2≤t≥T/2) 周期方波 ( ) ⎩ ( ) ⎨ ⎧ ≤ ≤ − − ≤ ≤ = A 0 t T/2 A T/2 t 0 x(t) 全波整流 x(t) ASinωt = 0

x(T) 周期抬数 x0=ea>0) x() 周期方形脉冲 4.求下列非周期信号的傅里叶变换，并绘出其频谱图 (1)指数函数x(t)=Ae"at(a>0,t≥0) (2)符号函数（下图中a,单位阶跃函数（下图中b) 10 (a) 6 提示：符号函数可记作S(),可先对 w-280 作傅里叶变换，变换后取极限入一0，就得到符号函数的傅里叶变化：单位阶跃函数 u(t)可看成是符号函数在纵坐标上平移而得。 (3) .4

·4· (4) x(t) t 2 T − 0 1 . 2 T . (5) x(t) t 2 τ − 0 1 . 2 τ . T 4． 求下列非周期信号的傅里叶变换，并绘出其频谱图 （1）指数函数 x(t)=Ae -at(a>0，t≥0) （2）符号函数(下图中 a)，单位阶跃函数(下图中 b) x(t) t 0 1 -1 x(t) t 0 1 (a) (b) 提示：符号函数可记作 Sgn(t)，可先对 ⎩ ⎨ ⎧ > − = − − 0 0 0 x(t) λ λ λ e t e t t t 作傅里叶变换，变换后取极限λ→0，就得到符号函数的傅里叶变化；单位阶跃函数 u(t)可看成是符号函数在纵坐标上平移而得。 （3） 周期指数 x(t) = e (a > 0) at (在-T/2，T/2 内) 注：用复指数计算 周期方形脉冲 讨论 T=3τ，T=5τ 时频谱图的变化

(t) 截断的余弦函数 x0= cos@ot T 并用图解法讨论T。T',TT'时，对频谱图的影响。 (4)指数衰减振荡信号x)=e-atcos 具有时移τ的三角脉冲 (按一种方法计算，另外列出 两种解法的思路) 具有时移τ和在原点的两 个方波脉冲 (7)绘出xt片AcOs(2t+D)+k,时域图和频谱图 求余弦脉冲的频谱 x()=)(/2) 0 (u≥x/2 5

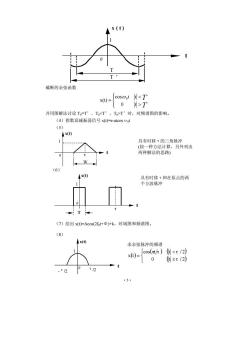
·5· x(t) t 0 1 T T ’ 截断的余弦函数 ⎪⎩ ⎪ ⎨ ⎧ > T’时，对频谱图的影响。 （4）指数衰减振荡信号 x(t)=e-atcosω0t （5） x(t) t 0 1 τ W （6） x(t) t 0 1 T τ （7）绘出 x(t)=Acos(2f0t+Φ)+k，时域图和频谱图。 （8） x(t) t 0 1 -τ/2 τ/2 具有时移τ的三角脉冲 (按一种方法计算，另外列出 两种解法的思路) 具有时移τ和在原点的两 个方波脉冲 求余弦脉冲的频谱 ( ) ( ) ( ) ( ) ⎩ ⎨ ⎧ ≥ < = 0 t τ / 2 cos t τ t τ / 2 x t π

9 (t) 求二余弦脉冲的频谱 10 x( 用图解方法求调制信号 x(t)=ecos ot (a>0,t≥0)经周期化后的频谱 己知一信号x)及其频谱如图1一5所示，现用其与 振荡信号cos2π6t(f>fm 相乘。（在这 习制信号 并示意画出调幅信号及 频谱】 ，本 图1-5 信号X40与40响关系如图1一6所示，已知0的频谱为X0.来信号X40的 。6

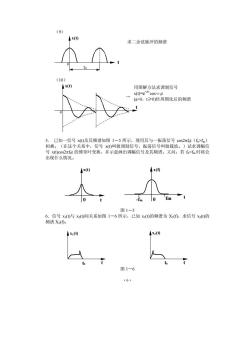
·6· （9） x(t) t 0 τ0 （10） x(t) t 0 . 5． 已知一信号 x(t)及其频谱如图 1－5 所示，现用其与一振荡信号 cos2πf0t（f0>fm） 相乘。（在这个关系中，信号 x(t)叫做调制信号，振荡信号叫做载波。）试求调幅信 号 x(t)cos2πf0t 的傅里叶变换，并示意画出调幅信号及其频谱。又问：若 f00，t≥0)经周期化后的频谱

7.图解法求卷积 1X(⑨ 1Xz(9 米 8.求(e-a)(e-)信号的傅里叶变换，并绘出其频谱图，(a0,b>0,D0. 9.对三个正弦信号x1)=cos2t,X2)=cos6t,x)=cos10mt,进行理想采样，采样 频率4Hz。求三个采样输出序列，比较三个结果，画出x0、x)和x)的时域波 形及采用点位置，并以频域图形解释频率混叠现象。 10.计算下列离散时间序列的DFT (0,/,/2,0,-1/,-1,-/2 11.用FFT算法求上题序列的频谱。试对此二题的结果作出解释。 l2.求(t)=Asint的概率密度函数，并绘出其曲线图。 13.求周期余弦信号x(t)=Acosoot的自相关函数和功率谱，并绘出其图形。 14.求方波和正弦波（见下图）的互相关函数。试与二正弦波相关的结果作比较，并分 析其原因。 7

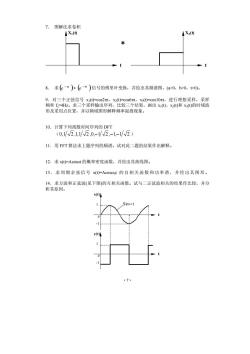
·7· 7． 图解法求卷积 X1(t) t X2(t) t 8． 求 ( ) ( ) at bt e e − − ∗ 信号的傅里叶变换，并绘出其频谱图，(a>0，b>0，t>0)。 9．对三个正弦信号 x1(t)=cos2πt，x2(t)=cos6πt，x3(t)=cos10πt，进行理想采样，采样 频率 fs=4Hz。求三个采样输出序列，比较三个结果，画出 x1(t)、x2(t)和 x3(t)的时域波 形及采用点位置，并以频域图形解释频率混叠现象。 10．计算下列离散时间序列的 DFT （0,1 2 ,1,1 2 ,0,−1 2 ,−1,−1 2 ） 11．用 FFT 算法求上题序列的频谱。试对此二题的结果作出解释。 12．求 x(t)=Asinωt 的概率密度函数，并绘出其曲线图。 13．求周期余弦信号 x(t)=Acosω0t 的自相关函数和功率谱，并绘出其图形。 14．求方波和正弦波(见下图)的互相关函数。试与二正弦波相关的结果作比较，并分 析其原因。 x(t) t 0 1 -1 y(t) t 0 1 -1 Sinωt *

15.设y-x2。试就x0,1,2,3,4,5。六个数据点计算x与y之间的相关系数 Py,并解释所得结果。 16.用图解法推演指数函数 x0)=e(≥0) 的离散傅里叶变换DT。已知x0及其频谱X(f)如愿图7-18所示。 O -t 0 1 析。设仅对信号中500以下频率成 分感兴趣 试求 (1)采样频率 (2)采样点数N (3)窗长T。 8

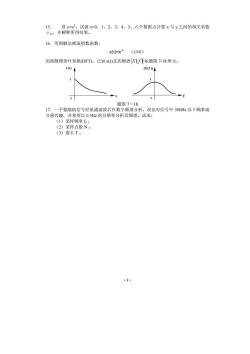
·8· 15． 设 y=x 2 。试就 x=0，1，2，3，4，5。六个数据点计算 x 与 y 之间的相关系数 ρxy，并解释所得结果。 16．用图解法推演指数函数： x(t)=e-t （t≥0） 的离散傅里叶变换(DFT)。已知 x(t)及其频谱 X ( f ) 如题图 7-18 所示。 x(t) t 0 1 |X(f )| f 0 1 题图 7－18 17．一平稳随机信号经低通滤波后作数字频谱分析。设仅对信号中 500Hz 以下频率成 分感兴趣，并希望以 0.5Hz 的分辨率分析其频谱。试求： （1）采样频率 fs 。 （2）采样点数 N 。 （3）窗长 T

第3章测试系统特性分析 1.一台压电式传感器的灵敏度SCp=9.OOPC/N,把它和一台灵敏度调到 Svc=0.005VPC的电荷放大器连接，然后接到灵敏度为Sxv=20mm/V的光线示波器上 记录。试画出仪器框图，并计算总灵敏度S。 2.一量程为50μA的微安表，校准时读数如下： 测量次数 2 3 4 5 标准表读数 10 2030 40 50 被校表读数 10 20.529.539 50.5 3.求题图2一3所示串联、并联和具有负反馈的测量系统的总灵敏度S。图中各环节 均为线性环节。 图2-3 4.用一个时间常数035秒的一阶装置（传递函数H=中云 1 )去测量周期分别 为1秒、2秒和5秒的正弦信号，问各种情况的相对幅值误差将是多少？ 5.一减速箱减速比为5：1，两齿轮转轴上各有其不平衡量，引起的振动在减速箱上 测得得信号为y),经频谱分析仪分析出其频谱图为Y(), 试答： 1

·1· 第 3 章 测试系统特性分析 1． 一台压电式传感器的灵敏度 Scp=9.00PC/N，把它和一台灵敏度调到 Svc=0.005V/PC 的电荷放大器连接，然后接到灵敏度为 Sxv=20mm/V 的光线示波器上 记录。试画出仪器框图，并计算总灵敏度 S。 2． 一量程为 50µA 的微安表，校准时读数如下： 测量次数 1 2 3 4 5 标准表读数 10 20 30 40 50 被校表读数 10 20.5 29.5 39 50.5 求该表的线性度(用最小二乘法回归) 若用计算机，试用 Matlab 语言编写此计算过程程序。 3．求题图 2－3 所示串联、并联和具有负反馈的测量系统的总灵敏度 S。图中各环节 均为线性环节。 x S1 S2 Sn x y S1 S2 Sn . . y S2 S3 y x S1 图 2－3 4． 用一个时间常数τ=0.35 秒的一阶装置（传递函数 ( ) s H s +τ = 1 1 ）去测量周期分别 为 1 秒、2 秒和 5 秒的正弦信号，问各种情况的相对幅值误差将是多少？ 5．一减速箱减速比为 5：1，两齿轮转轴上各有其不平衡量，引起的振动在减速箱上 测得得信号为 y(t)，经频谱分析仪分析出其频谱图为 Y(f ) ， 试答： y(t) t |Y(f)| f(Hz) 10 20 30 40 50