《信号与系统》课程教学资源（习题解答）第一章 信号与系统概述

第一章信号与系统概述本章重点（1）信号的函数表示与图形表示；单位冲激信号与冲激偶信号；2（3）信号基本运算与信号分解；系统的性质；(4)(5)线性系统的方框图表示。例1.1试概略画出下列各函数表示式表示的信号的波形图：(a) .()(1 + 2)- ε(t -2)in 2m[e()-e(t-2)](b) f,(d)-解按照给定的函数表示式，求出信号的初值、终值、极大值、极小值和一些关键点的信号值，按照上述各值可概略画出信号的波形图。(a)可求出J(0)=0，J(2)=1，J(-2)=1，其他f()=0，故可画出f()信号的波形图如图1.1.1所示。t.()（b）由f(的表示式可知f,0）定义在t=0至t=2区间内，其包络在t=0时为1，在1=2时为0，故J,(）信号的波形图如图1.1.2所示图11

第一章 信号与系统概述 本章重点 （1） 信号的函数表示与图形表示； （2） 单位冲激信号 与冲激偶信号； （3） 信号基本运算 与信号分解； （4） 系统的性质； （5） 线性系统的方框图表示。 例 1.1 试概略画出下列各函数表示式表示的 信号的波形图： （a） ( ) [ ] ( )( ) 2 2 2 1 = t + − t − t f t ε ε （b） ( ) sin 2 [ ] () ( ) 2 2 2 1 − −         = − t t t t f t π ε ε 解 按照给定的函数表示式，求出信号的初值、终值、极大值、极小值和一些关键点的信号 值，按照上述各值可概略画出信号的波形图。 （a）可求出 ( ) 0 0 f1 = ， ( ) 2 1 f1 = ， ( 2) 1 f1 − = ，其他 f (t) = 0 ，故可画出 f ( )t 信号的 波 形图如图 1.1.1 所示。 （b）由 f ( )t 2 的表示式可知 f ( )t 2 定义在t = 0 至t = 2 区间内，其包络在t = 0 时为 1，在 t = 2时为 0，故 f ( )t 2 信号的 波形图 如图 1.1.2 所示 图 1 .1 .2 f (t ) 2 1 1 2 0 t 0 t 图 1 .1 .1 − 2 2 1 ( ) f t 1

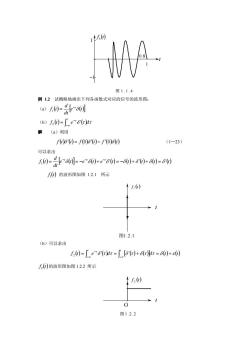
1t.()11例1.2试概略地画出下列各函数式对应的信号的波形图：(a) 1()=%[e~0)](b) :(0)-e8'(t)t解 (a) 利用1(08'(0)= (0)5'(0)- f(0)6(0)(123)可以求出(0)=[6(0)=-~()+e*80)=-80)+80)+6()=8)(）的波形图如图1.2.1所示+f(0)图1.2.1（b）可以求出S(0)= e"8(t)dt = , [6(t)+8(t)t = 8(0)+e()f()的波形图如图1.2.2所示1.0)0图1.2.2

0.8 1 图 1 . 1 . 4 t f ( )t 4 −1 1 例 1.2 试概略地画出下列各函数式对应的信号的波形图： （a） ( ) [ ] e ( )t dt d f t t δ − 1 = （b） () ( ) δ τ τ τ f t e d t ∫−∞ − = ′ 2 解 （a）利用 f () () ( ) () t δ ′ t = f 0 δ ′ t − f ′(0)δ (t) （1—23） 可以求出 ( ) [ ] e ( )t e () () () () () () t e t t t t t dt d f t t t t = δ = − δ + δ ′ = −δ + δ ′ + δ = δ ′ − − − 1 f ( )t 1 的波形图如图 1.2.1 所示 f (t) 1 t 图1.2.1 （b）可以求出 f () ( ) ( ) ( ) t e d [ ]d () () t t t t δ τ τ δ τ δ τ τ δ ε τ = ′ = ′ + = + ∫−∞ ∫−∞ − 2 f ( )t 2 的波形图如图 1.2.2 所示 O f (t) 2 t 图 1 .2 .2

例1.3试求出下列函数值：(a) f:()= 2:(2t+4)6(t+ 2)(b) f:(0)-(2-4t+3)dt解（a）可以求得(0)= 28(2t + 4)6(++2)= 28(2(-2)+4)o(+2)=2s(0)(++2)注意到s(0)=0.5,故f,(0)=8(t+2)(b）解此题要注意单位冲激信号6(°-4t+3)的性质，由于(2 - 4t +3)= (t-1)(t-3) 故当1=1及1=2时，6(°-41+3)存在二个冲激，而当1为其他值时，6(2-41+3)=0，因此:(0)= [ o(2 - 41+ 3)dt = [ o[6(-1)+ 8(- 3)]dt= 2例1.4一连续信号的波形图如图1.4.1所示，试画出下述信号27-2的波形图并标注座标值：10)0图1.4.1解2-2的波形图如图1.4.3所示图1.4.3

例 1.3 试求出下列函数值 ： （a） () ( ) ( ) 2 2 4 2 f1 t = ε t + δ t + （b） ( ) ( ) ∫ ∞ −∞ f t = t − 4t + 3 dt 2 2 δ 解 （a）可以求得 () ( ) ( ) 2 2 4 2 2 (2( 2) 4) ( 2) 2 (0)( ) 2 f1 t = ε t + δ t + = ε − + δ t + = ε δ t + 注意到ε ( ) 0 = 0.5 ，故 () ( ) 2 f1 t = δ t + （b）解此题要注意单位冲激信号 ( 4 3) 2 δ t − t + 的性质， 由于 ( 4 3) ( ) 1 ( 3) 2 t − t + = t − t − 故当 t = 1 及 t = 2 时， ( 4 3) 2 δ t − t + 存在二个冲激，而当 t 为其他值时， ( 4 3) 0 2 δ t − t + = ，因此 ( ) ( ) 4 3 [ ] ( )( ) 1 3 2 2 2 = − + = − + − = ∫ ∫ ∞ −∞ ∞ −∞ f t δ t t dt δ δ t δ t dt 例 1.4 一连续信号 的波形图如图 1.4.1 所示，试画出下述信号       − 2 2 2 t f 的波形图， 并标注座标值： − 2 O 2 1 f (t) t 图 1 .4 .1 −1 1 解       − 2 2 2 t f 的波形图如图 1.4.3 所示 2 4 6 8 图 1 .4 . 3 t       − 2 2 2 t f O 2

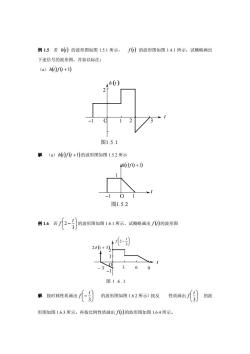
例1.5若h(）的波形图如图1.5.1所示，(）的波形图如图1.4.1所示，试概略画出下述信号的波形图，并加以标注：(a) h()r(t+1)(t)图1.5.1解a）h(0)r(t+1)的波形图如图1.5.2所示th(0)r(t+1)图1.5.2例 1.6若(2-岁)的波形图如图1.6.1所示，试概略画出「0)的波形图图1.6解按时移性质画出（--)的波形图如图1.6.2所示）按反性质画出的沉3形图如图1.6.3所示。再按比例性质画出f()的波形图如图1.6.4所示

例 1.5 若 h( )t 的波形图如图 1.5.1 所示， f (t) 的波形图如图 1.4.1 所示，试概略画出 下述信号的波形图，并加以标注： （a） h() ( ) t f t +1 −1 1 2 2 图1.5.1 t h (t ) O 3 解 （a） h() ( ) t f t +1 的波形图如图 1.5.2 所示 O h(t)f (t +1) t 图1.5.2 1 −1 1 例 1.6 若       − 3 2 t f 的波形图如图 1.6.1 所示，试概略画出 f (t)的波形图 − 3 3 6 O       − 3 2 t f t 图 1 . 6 . 1 1 2δ ( ) t + 3 −1 9 2 解 按时移性质画出       − 3 t f 的波形图如图 1.6.2 所示〉按反 性质画出       3 t f 的波 形图如图 1.6.3 所示。再按比例性质画出 f (t)的波形图如图 1.6.4 所示

(-)28(t+9),图1.6.228(t-9)o(t-3图1.6.3图1.6.4其中冲激信号按比例变化后，其幅度要产生相应变化，即(at)=o()1e可按(an)= 0(at)dt ="(t)dt=-:()a得到证明，因此28(31-9)=28[3(t-3)]-28( -3) 例1.7对于下述的连续信号，输入为e(d)，输出为r(d)，T[e()]表示系统对 e()的响应，试判定下述系统是否为；（1）线性系统：（2）非时变系统；（3）因果系统；（4）稳定系统：(a) r(0)=T[e(0)]=e(t-2)(b) r(0)= T[e()]=e(-0)解(1-26)T[ae;(0)+a,e2(0)=ar()+a,r()若满足（1-26）式则为线性系统，否则为非线性系统，判断系统是否为非时变系统，则按（1-27）式T[e(-10)]=r(t-10)(1-27)若满足（1一27）式则为非时变系统，否则为时变系统。对于一般系统，判断其是否为因果系统，则按其输出变化不发生在输入变化之前的系统为因果系统，否则为非因果系统。对于线性非时变系统，若满足t<0时，系统的冲激响应h(0)=0的系统为因果系统，否

2 − 9 −1 2δ ( ) t + 9 1 图1.6.2 t       − 3 t f − 6 − 3 O 3 6 2 9 −1 2δ (t − 9) 1 图 1 .6 .3 t       3 t f O 3 − 3 2 2 −1 ( ) t 3 3 2 δ − 1 图1 .6 .4 t f (t) −1 O 1 其中冲激信号按比例变化后，其幅度要产生相应变化，即 ( ) ( )t a δ at δ 1 = 可按 () ( ) ( ) ( )t a d a at a d t t δ δ τ τ δ τ τ δ 1 1 = ′ = ′ = ∫−∞ ∫−∞ 得到证明，因此 ( ) () [ ] ( ) 3 3 2 2δ 3t − 9 = 2δ 3 t − 3 = δ t − 例 1.7 对于下述的连续信号，输入为e(t) ，输出为 r(t) ， T[e(t)]表示系统对 e(t) 的响应，试判定下述系统是否为： （1） 线性系统：（2）非时变系统；（3）因果系统；（4）稳定系统： （a） r() () t = T[ ] e t = e( ) t − 2 （b）r() () t = T[ ] e t = e( ) − t 解 T[ ] a e () () t a e t a r ( )t a r (t) 1 1 + 2 2 = 1 1 + 2 2 （1—26） 若满足（1—26） 式则为线性系统，否则为非线性系统，判断系统是否为非时变系统，则 按（1—27）式 [ ] ( ) ( ) 0 0 T e t − t = r t − t （1—27） 若满足（1—27）式则为非时变系统，否则为时变系统。对于一般系统，判断其是否为因果 系统，则按其输出变化不发生在输入变化之前的系统为因果系统，否则为非因果系统。对于 线性非时变系统，若满足t < 0 时，系统的冲激响应 h(t) = 0 的系统为因果系统，否

则为非因果系统。对于一般系统，判断其是否为稳定系统则按 BIBO准则，即输入有界，则输出有界的系统为稳定系统。对于线性非时变系统，若满足/n(0)di0时，输出变化1发生在输入变化（-7）之后，该系统为因果系统。而当1<0时，输出变化发生在输入变化之前，该系统为非因果系统。该系统满足BIBO准则，故该系统为稳定系统。例1.8试用加法器、系统乘法器和积分器画出下述微分方程所表示的系统得方框图：0+20+2%0+0-20+30d解先研究

则为非因果系统。 对于一般系统，判断其是否为稳定系统则按 BIBO 准则，即输入有界，则输出有界的系 统为稳定系统。对于线性非时变系统，若满足 ( ) ∫ ∞ −∞ h t dt 0 时，输出变化t 发生在输入变化(− t) 之后，该系统为因 果系统。而当t < 0 时，输出变化发生在输入变化之前，该系统为非因果系统。该系统满 足 BIBO 准则，故该系统为稳定系统。 例 1.8 试用加法器、系统乘法器和积分器画出下述微分方程所表示的系统得方框图： ( ) ( ) () () x() () t x t dt d y t y t dt d y t dt d y t dt d 2 2 3 2 2 3 3 + + + = + 解 先研究

d3r(0)+2r()+2r()+r(0)= x(0)利用算子d-.p's,及p"-L(YIt0=.pdt-上式可表示为p"r(0)+2p"r()+2pr(0)+r()=x(0)于是r(0)=p-[(0)-2p'r()-2pr(0)-r(0)]上式可表示为如图1.9.1所示+r(0)(0)pl?图1.9.1将给定的微分方程写成算子形式：p*(0)+2p*y()+2py()+y(0)= px()+3x()将x()=p"r()+2p*r()+2pr()+r(0)代入上式，得p's(0)+2p*y(0)+2p()+(0)=plp'r0)+2p*r()+2pr()+r()+3[p*r()+2p?r(0)+2pr(0)+r(0)]= p'[pr(c)+ 3r(0)]+2 p"[pr(0)+ 3r(0)]+ 2 p[pr(0)+ 3r(0)]+[pr()+ 3r(0)]对比等式两边，可得()= pr(0)+3r(0)因此，本系统可用图1.9.2所示的方框图来表示

( ) ( ) r() () () t r t x t dt d r t dt d r t dt d + 2 + 2 + = 2 2 3 3 利用算子 p ( )dτ dt d p dt d p dt d p t ∫−∞ − = = = =1 3 3 3 2 2 2 , , ,及 上式可表示为 p r( )t + 2 p r(t)+ 2 pr(t) + r(t) = x(t) 3 2 于是 r( )t = p [x(t) − p r(t)− pr(t) − r(t)] − 2 2 3 2 上式可表示为如图 1.9.1 所示 ∑ 2 2 −1 p −1 x( )t p −1 p 图1.9.1 r(t) 将给定的微分方程写成算子形式： p y( )t 2 p y(t) 2 py(t) y(t) px(t) 3x(t) 3 2 + + + = + 将 x() () () () t = p r t + 2 p r t + 2 pr t + r(t) 3 2 代入上式，得 () () () ( ) [ ] () () () () [ ] () () () () p [ ] pr() () t r t p [ ] pr() () t r t p[ ] pr() () t r t [ ] pr() () t r t p p r t p r t pr t r t p r t p r t pr t r t p y t p y t py t y t 3 2 3 2 3 3 2 2 3 2 2 2 2 3 2 3 2 3 2 3 2 = + + + + + + + = + + + + + + + + + + 对比等式两边，可得 y(t) = pr(t)+ 3r(t) 因此，本系统可用图 1.9.2 所示的方框图来表示

r(t)00x(0)p-!p2O图1.9.2

+ 3 ∑ y ( t ) r ( t ) 图 1 . 9 . 2 − 1 x( )t p − 1 p − 1 p 2 2 ∑