《电路》课程教学资源（PPT课件）第18章 分布参数的电路

第19章分布参数的电路 §1.分布参数和分布参数电路 实际电路中参数具有分布性，必须考虑参数分布性的电路， 称为分布参数电路。 + 例：室内1500m电线 u u2 f=50 Hz 3×108 =6000km 1500m f50 延时时间 t'≤1500 3×108 =5×106s u =Um sin 100t 42=Um sin100元(t-0.000005) =U sin(100πt-0.0005π) U1≈u2 =U sin(100πt-0.09) 1500m的输电线处理为集总参数电路

例 ： 室内1500m电线 f =50 Hz 6000 km 50 3 108 =  = = f v  u1 u2 1500m + + - - 1500m的输电线处理为集总参数电路 延时时间 5 10 s 3 10 1500 6 8 − =   t = u U sin100 t 1 = m sin(100 0.09 ) sin(100 0.0005 ) sin100 ( 0.000005) m m 2 m  = − = − = − U t U t u U t     u1 u2 § 1.分布参数和分布参数电路 第19章 分布参数的电路 实际电路中参数具有分布性，必须考虑参数分布性的电路， 称为分布参数电路

1500km的输电线 + u 延时时间 1-150000-5×10s 0 3×108 1500km 41=Um sin100πt 4,=U sin10(0x(t-0.00s)=U sin(100元t-〉 1500km的输电线处理为分布参数电路

u U sin100 t 1 = m ) 2 2 m sin100 ( 0.005) m sin(100  u = U  t − = U  t − 1500km的输电线处理为分布参数电路 1500km的输电线 u1 u2 1500km + + 延时时间 - - 5 10 s 3 10 1500000 3 8 − =   t =

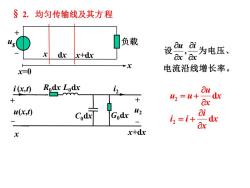
§2.均匀传输线及其方程 负载 dx x+dx oui为电压、 Ox'ax X=0 电流沿线增长率。 i(x,t) Rodx Lodx - 3u + u2=W+ dx ax u(x,t) Codx Godx W2 ai 2=i+ o dx Ox X x+dx

电流沿线增长率。 设 为电压、 x i x u     , x x i i 2 i d   = + x x u u2 u d   = + x dx x+dx x us 负载 + - x=0 i2 x C G0dx 0dx R0dx L0dx u2 i(x,t) u(x,t) x+dx + - - + § 2. 均匀传输线及其方程

ou = 0i 沿线电压减少率等于单位长度上 Ex Roi+Lo 8t 电阻和电感上的电压降。 Oi &x =Gou+Co Ou 沿线电流减少率等于单位长度上 Ot 漏电流和电容电流的和。 对t自变量给定初始条件：u(c,O),i(c,0) 对x自变量给定边界条件：u(0,t),i(0,t) 解出u,i u(l,t),i(l,t)

t i R i L x u   = +   − 0 0 沿线电压减少率等于单位长度上 电阻和电感上的电压降。 t u G u C x i   = +   − 0 0 沿线电流减少率等于单位长度上 漏电流和电容电流的和。 对t自变量给定初始条件：u (x , 0) , i (x , 0) 对x自变量给定边界条件：u (0 , t ) , i (0 , t ) u (l , t ) , i (l , t ) 解出 u , i

§3均匀传输线的正弦稳态解 一.相量方程 us =Um sin at i(x,t) u=v2U(x)sin(at+v,(x)) ① u(x,t) i=2I(x)sin(at+v;(x)) t=0 有效值和初相位是位移x的函数 u(x,t)-→U(x) i(x,t)→1(x) 简记为：0,1

u U t S = m sin 2 ( )sin( ( )) 2 ( )sin( ( )) i I x t x u U x t x i u     = + = + U I   简记为： , § 3 均匀传 输线的正弦稳态解 一. 相量方程 t=0 x us u(x,t) i(x,t) + - + - u(x,t) U(x) →  i(x,t) I(x) →  有效值和初相位是位移 x 的函数

代入方程 ∂u Oi 0 =(Ro+jaLo)i=Zoi Ox =Roi+Lo 8t Oi =Gou+Co Ou &x 业=G+joC,0=r0 dx Z0=R0+jωL0单位长度串联阻抗 Yo=G0+jwC0单位长度并联导纳 注意：乙。 Yo

代入方 程 t i R i L x u   = +   − 0 0 t u G u C x i   = +   − 0 0 0 0 L0 Z = R + j 单位长度串联阻抗 0 0 C0 Y = G + j 单位长度并联导纳 0 0 1 Y 注意：Z         − = + = − = + = G j C U Y U x I R j L I Z I x U       0 0 0 0 0 0 ( ) d d ( ) d d  

二.均匀传输线的正弦稳态解 d20 dI dr2 = 两边对x求导 dx dx d'j dl =YU dr2 dx dx d'U dx2 =-ZY0 令y=VZ。=a+jp d'j dx2 =-ZoKi Y为均匀传输线的传播系数 dv dx2 -y20=0 特征方程为：p2-y2=0 d'j dx7-ri=0 p=±Y 解答形式为：U=Ae+A,e

令 = Z0 Y0 = + j  为均匀传输线的传播系数 二. 均匀传输线的正弦稳态解        − = − = Y U x I Z I x U     0 0 d d d d        − = − = x U Y x I x I Z x U d d d d d d d d 2 0 2 2 0 2     两边对x求导        − = − − = − Z Y I x I Z Y U x U     2 0 0 2 2 0 0 2 d d d d 特征方程为：   =  − = p p 0 2 2        − = − = 0 d d 0 d d 2 2 2 2 2 2 I x I U x U       解答形式为： x x U A A   e e = 1 + 2 − 

dU Zol 1 i- 1 Zo dx Zo (-Ayex+Ayer)=(d er-Aers) Zo 令2名 Z为特性阻抗（波阻抗） 解答形式为： U(x)=Ajer*+Azerx i(x)=(Aerx-Azer*)/Zc 由边界条件确定A1,A,人 始端电压、电流已知 终端电压、电流已知

Z I x U   0 d d − = x x ） A x A x ） Z A A x Z U Z I      (  e  e ( e e 1 d 1 d 1 2 0 1 2 0 0 = − = − − + = − − −   0 0 0 0 0 0 Y Z Z Y Z Z ZC = = =  令 Zc为特性阻抗( 波阻抗 ) 由边界条件确定A1 ，A2 始端电压、电流已知 终端电压、电流已知 解答形式为：     = − = + − − C x x x x I x A A Z U x A A ( ) ( e e )/ ( ) e e 1 2 1 2      

()已知始端(x=0)电压0(0)=U1、电流i(0)=i1 将x=0代入 0(0)=U1=A1+A 4=+z i(0)=i1=(A1-A2)1Zc 4=o,-z 0xw)=20+zie+20,-Z1e 0圪+x-授-e i(x)Ze U(x)=U chyx-Zci,shyx -0shyx+i,chy x

(1)已知始端(x = 0 )电压 、电流 1 I(0) I  =  (0) U U1  =         = − = + ( ) 2 1 ( ) 2 1 2 1 1 1 1 1 A U Z I A U Z I C C            = + − − = + + − − − x C x C x C x C I Z U I Z U I x U x U Z I U Z I     ( )e 2 1 ( )e 2 1 ( ) ( )e 2 1 ( )e 2 1 ( ) 1 1 1 1 1 1 1 1               = = − = = + A A ZC I I U U A A (0) ( )/ (0) 1 1 2 1 1 2     将 x = 0 代入      + − = = − x I x Z U I x U x U x Z I x C C     ( ) s h ch ( ) ch s h 1 1 1 1      

(2)已知终端x=1)电压U()=02、电流i()=2 将x=1代入方程 [U(0=U2=A,e”+A,e 4=0,+z1,” i0=i2=(A,e”-A,e')/Zc A=20,-Z1)e1 传输线上距始端距离x处电压、电流为 0e)-20+Z4e+0.-Z1,ew =g+e-2-

(2) 已知终端(x = l )电压 、电流 2 I(l) I  =  ( ) U2 U l  =      = = − = = + − − C l l l l I l I A A Z U l U A A ( ) ( e e )/ ( ) e e 2 1 2 2 1 2         将 x = l 代入方程 l C l C A U Z I A U Z I   − = − = + ( )e 2 1 ( )e 2 1 2 2 2 1 2 2     ( ) 2 ( ) 2 2 2 ( ) 2 2 ( ) 2 2 ( )e 2 1 ( )e 2 1 ( ) ( )e 2 1 ( )e 2 1 ( ) l x C l x C l x C l x C I Z U I Z U I x U x U Z I U Z I − − − − − − = + − − = + + −               传输线上距始端距离x 处电压、电流为