《信号与系统》课程授课教案（课件讲稿）第1章 信号与系统

信号与系锁电车派第一章信号与系统81-1绪论信号与系统一、信号传输系统1、消息和信号消息：语言、文字、图画、编码等信号：把消息转变成便于处理的光、电（随时间变化）2、通信系统的典型构成三、 信号与系统学科待发接收输入信号输出信号精鱼酸热量人及射机面过医收机胰换病消息、信号理论：信号分析：讨论信号的表示、信号的性质任务：传送消息信号处理：信号综合：例：电话：语言或音乐（消息）电流或电2、系统理论：压(信号)一接收端一电信号还原为声音系统分析：对于给定的系统，在输入信号作用下产生的输出信号81-2信号“信号"与“函数（或序列）”两个词互相通用系统综合：给定性能指标，设计一个满足性能指标的系统。一、信号的分类1、连续信号和离散信号3、与其它学科的关系连续信号：在连续时间范围内(-<t<)血烈究相性理治、混体聚(输型定义的信号f(t)=10sint论打下基础。例：1026

1 信号与系统电子课件 1、消息和信号 第一章 信号与系统 §1-1绪论 一、信号传输系统 消息：语言、文字、图画、编码等 2、通信系统的典型构成 信号：把消息转变成便于处理的 光、电（随时间变化） 任务：传送消息 转换器 转换器 发射机 信道 接收机 待发 消息 输入信号 输出信号 接收 消息 例：电话：语言或音乐（消息） 电流或电 压(信号) 接收端 电信号还原为声音 二、信号与系统学科 1、信号理论： 2、系统理论： 信号处理： 信号综合： 信号分析：讨论信号的表示、信号的性质 系统分析：对于给定的系统，在输入信 号作用下产生的输出信号 系统综合：给定性能指标，设计一个满 足性能指标的系统。 3、与其它学科的关系 为研究网络理论、通信理论、控制 理论、信号处理和信号系统检测理 论打下基础。 §1-2信号 “信号”与“函数（或序列）” 两个词互相通用。 一、信号的分类 1、连续信号和离散信号 连续信号：在连续时间范围内 定义的信号 (−∞ < t < ∞) 0 1 2 -10 10 t f (t) 10 sin t 1 = 例：

离散信号：在离散瞬间有定义的信号fe(k)例：[f(k)回口1酒0T0k=-0f(k)=k=0k=0,12,.可见：信号的值可以是连续0.5k=1的，也可以不是时间间隔：T,=1-2、周期信号和非周期信号3、确定信号和随机信号周期信号：周而复始，无始无终确定性信号：y=f(t)F(t+mT)= f(0), m=0,±1,±2, 连续信号：随机信号：信号不遵循确定的规律离信，(k)=(+mN）=0,±1,±2,191(a)半波整流信号(b)锯齿序列N:周期T：周期*二、基本信号f(t)┌Aet≤0(0)f(0)=1、连续信号-0t>0①正弦信号b.双边指数信号AIf(t) = Asin(ot +g)α>0-Aeat≤0f(t)=f(t)②指数信号-Ae-at≥01f(0)a.单边指数信号c.复指数信号ANF(t)= Ae(a+j0) = Ae"ejar_Ae-α t≥0f.(t) =^L0t0而 eja" =cosat+jsinot

2 f2(t)= 0 1, 1, 0, − 3 1 3 1 1 1 > 0 k =0,1,2," f 1(k)= 0.5 2 1 0 1 0 1 1 = = = − 0 t A f2(t) = 0 t Aeα 0 0 > ≤ t t f (t) = t t Ae Ae α α − 0 0 ≥ ≤ t t j t t j t f t Ae Ae e α ω α ω = = ( + ) ( ) b.双边指数信号 c.复指数信号 e t j t j t ω ω ω 而 = cos + sin f (t) t 1 A ( ) 2 f t t α > 0

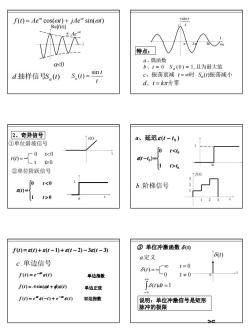
f(t)= Ae" cos(ot) + jAe" sin(ot)Ref(t)]A.一特点：a、偶函数K0b、t=0 S(0)=1,且为最大值sintC、振荡衰减 t=o0时 Sa(0)振荡减小d.抽样信号s.()S.(t) =d、t=k元为零2、奇异信号a、延迟e(t-t)rt①单位斜坡信号0tt②单位阶跃信号f()ot0t③单位冲激函数 8(t)f(t)=e(t)+8(t -1)+ e(t - 2) - 3e(t - 3)s(t)a.定义c.单边信号t=08()=478-0I(t) =e-" 8(t)t+0单边指数[s(t)dt =1f(t)= Asin(at + p)e(t)单边正弦f(t)= ee(-t)+e-" s(t)双边指数说明：单位冲激信号是矩形脉冲的极限36

3 d. S (t) 抽样信号 a t t S t a sin ( ) = α < − = 0 0 0 1 0 ( ) t t t t ε t t t0 1 b .阶梯信号 t 1 2 3 1 2 3 f (t) ( ) 0 a、延迟ε t − t f (t) = ε(t) + ε(t − 1) + ε(t − 2) − 3ε(t − 3) c .单边信号 f (t) e (t) t ε −α = 单边指数 f (t) = Asin(ωt + φ)ε (t) 单边正弦 f (t) e ( t) e (t) t t ε ε α −α = − + 双边指数 δ (t) = 0 t 0 0 ≠ ∞ t = ( ) =1 ∫ +∞ −∞ δ t dt a.定义 δ (t) t 0 说明：单位冲激信号是矩形 脉冲的极限 ③ 单位冲激函数 δ (t)

ft单位延迟冲激函数t=to8(t-to) =t+t.8(t-t)-dt =1.f (t)= -[e(t + ) - 8(t - )6(e(+-()36b.性质f(t)s(t- to)dt = f(to)1)f(t)8(t) = f(0)8(t)2)取样性质[ f(t)8(t)dt = f(0)Hf(o(roOF+3) (1)=(-1)偶函数④单位冲激偶函数'(t)）尺度特性1(t)8(1)8(at)=(a + 0)de(t)8'(t) =dtV) e(t)与 (t)关系de(t)8(t)= f8(t)dt8(t) =dtd

4 )] 2 ) ( 2 [ ( 1 ( ) τ ε τ ε τ f t = t + − t − f (t) τ 1 2 τ 2 τ − 0 t )] 2 ) ( 2 [ ( 1 ( ) τ ε τ ε τ δ t = lin t + − t − τ →0 单位延迟冲激函数 0 t0 t δ (t − t0 ) = 0 0 0 t t ≠ ∞ t = t ( − 0 ) ⋅ = 1 ∫ +∞ −∞ δ t t dt 2) 取样性质 b.性质 f (t) (t)dt = f (0) ∫ +∞ −∞ δ 1） f (t)δ (t) = f (0)δ (t) t f (0) 0 ( )0 f t ( ) ( ) ( ) 0 0 f t t − t dt = f t ∫ +∞ −∞ δ 3） δ(t) =δ(−t) 偶函数 4）尺度特性 ( ) ( 0) 1 ( ) = t a ≠ a δ at δ Ⅴ）ε(t)与δ (t)关系 ∫−∞ = t ε (t) δ (t)dt dt d t t ( ) ( ) ε δ = dt d t t ( ) ( ) δ δ ′ = ④单位冲激偶函数 δ ′(t) ( ) ' δ t

特性( f(t)s(t-to)dt=-f(to)同取样性质+f(t)s'(t)dt()8"(0)dt =(-1)" f"(0)= f(t)8(1)- f'(0)s(t)dt =-f'(0)例：计算下列各题b.比较ts'(n)18(0)1ro(1)[ + sin()]8(t+2)dt00 (t +2F -2t+1)8(t-1)dt(2)e(0)= dr()8(1) = de()0(0)=d00)解：(原式[+sin()-=- 3in(e(0)-,8(0)dt80)= 8(0dr(t)-s(0)dt(2)原式= -[3t° +4t-2] = =-5③符号函数2.离散信号1>0定义sgn(t) =①单位样值序列-1 1<0Sgn(t)k=0-定义s(k)=L。1其它回sgn(t) = 8(t) - 8(-t)

5 ∫ +∞ −∞ f (t)δ ′(t)dt = f (t) (t) − f ′(t) (t)dt = − f ′(0) ∫ +∞ −∞ +∞ δ −∞ δ 特性 取样性质 ( ) ( ) ( 1) (0) n n n f t t dt = − f ∫ +∞ −∞ δ ( ) ( ) ( ) 0 0 f t ′ t −t dt = − f ′ t ∫ +∞ −∞ 同 δ 理 t r(t) t δ ′(t) t δ (t) ⑴ dt dr t t ( ) ε ( ) = dt d t t ( ) ( ) δ δ ′ = dt d t t ( ) ( ) ε δ = b .比较 t 1 ∫−∞ = t r(t) ε (t)dt ∫−∞ = t ε (t) δ (t)dt ∫−∞ = ′ t δ (t) δ (t)dt t dt t t )] ( 2) 4 [ sin( 2 + + − ∞ ∞ ∫ δ π 例:计算下列各题 （1） （2） (t 2t 2t 1) (t 1)dt 3 2 + − + ′ − −∞ ∞ ∫ δ 解：（1）原式= )] 3 4 [ sin( 2 2 + t = − = t t π （2）原式= [3 4 2] 5 1 2 − t + t − t= = − ⑤符号函数 sgn( t) = 1 0 1 0 − t t 定义 sgn(t) = ε(t) − ε(−t) t +1 -1 Sgn(t) δ (k) = 0 1 k = 0 定义 其它 ① 单位样值序列 -3 -2 -1 1 2 3 1 2. 离散信号

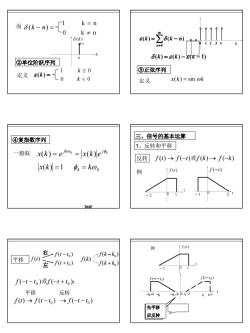
k= n广1而 s(k-n)=LOk+n8(k)e(k)= 2o0k8(k)=8(k)-E(K=1)②单位阶跃序列③正弦序列k≥0定义 e(k)=k<0x(k) = sin ok定义三、 信号的基本运算④复指数序列1、反转和平移-般取 x(k)=ejkoo =|x(k)lej反转f(l) →f(-1)或f(k) → f(-k)x(k)=1Φk=koof(0)f(-t)E1右f(t-to)f(k-ko)平移()-f(k+k)左(+1)(-1-lo(-)f(-t -to)或f(-t+to):平移反转f(t)-→f(t-to) →f(-t-to)先平移后反转

6 0 k n 1 k n ≠ = 而 δ (k − n) = ②单位阶跃序列 0 0 1 0 < ≥ k k 定义 ε (k) = δ (k ) (1) n k ∑ ∞ = = − 0 ( ) ( ) n ε k δ k n δ (k) = ε (k) − ε (k − 1) ③正弦序列 定义 x(k ) = sin ωk 0 1 2 3 4 k 0 x(k) =1 φ k = kω ④复指数序列 k jk j x k e x k e ω φ ( ) ( ) 0 一般取 = = 1、反转和平移 反转 f (t) → f (−t)或f (k) → f (−k) 0 2 t − 1 例 f (−t) 1 t 0 − 2 f (t) 三、信号的基本运算 f (k) ( ) ( ) 0 0 f k k f k k + − 平移 f (t) ( ) ( ) 0 0 f t t f t t + − 左 右 ( ) ( ) f −t − t0 或f −t + t0 ： ( ) 0 → f −t − t 平移 反转 ( ) ( ) 0 f t → f t − t 例 1 t − 2 0 f (t ) 0 t 0 −2 1 t 0+ 0 t 0 −t ( 2) −(t 0+1) − t 0− t 先平移 后反转 ( ) 0 f −t − t ( ) 0 f t − t

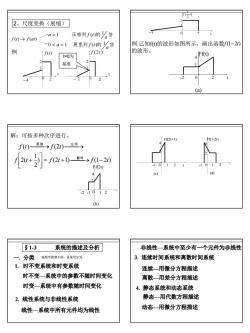
G2、尺度变换（展缩）压缩到F(0)的%倍a>f(t)-→ f(at)例：已知(t)的波形如图所示，画出函数f(1-21)*0<a<展宽到f()的%倍的波形。例f(2t)Ff(t)=0基淮解：可按多种次序进行。(2t+1)1-2F(1)—展缩→F(21)—左移)2(+)=(21+)血址→(-21):1.0Ff(2t)(c)(d)2-1(b)$1-3非线性一系统中至少有一个元件为非线性系统的描述及分析一，分类按数学模型不同，系统可分为3.连续时间系统和离散时间系统1. 时不变系统和时变系统连续一用微分方程描述时不变一系统中的参数不随时间变化离散一用差分方程描述时变一系统中有参数随时间变化4.静态系统和动态系统静态一用代数方程描述2.线性系统与非线性系统动态一用微分方程描述线性一系统中所有元件均为线性

7 2、尺度变换（展缩） f (t) → f (at) 展宽到 的 倍 压缩到 的 倍 a a f t a a f t 0 1 ( ) 1 1 ( ) 1 例 2 t 0 − 4 f (t) 1 2 t 2 − 2 0 f (2t) 1 2 t=0为 基准 4 0 t − 8 ) 2 1 f ( t 1 2 例:已知f(t)的波形如图所示，画出函数f (1−2t) 的波形。 Ff(t) -2 0 2 2 4 t (a) -2 0 2 2 4 Ff(2t) t (b) -1 1 解：可按多种次序进行。 ) (2 1) (1 2 ) 2 1 f 2(t = f t + → f − t       + 翻转 f (t) 展缩→ f (2t) 左移→ 0 2 4 Ff(2t+1) t (c) -1 1 2 0 2 4 Ff(1-2t) t (d) -1 1 2 §1-3 系统的描述及分析 一. 分类 按数学模型不同，系统可分为 1. 时不变系统和时变系统 2. 线性系统与非线性系统 时变—系统中有参数随时间变化 时不变—系统中的参数不随时间变化 线性—系统中所有元件均为线性 非线性—系统中至少有一个元件为非线性 3. 连续时间系统和离散时间系统 连续—用微分方程描述 离散—用差分方程描述 4. 静态系统和动态系统 动态—用微分方程描述 静态—用代数方程描述

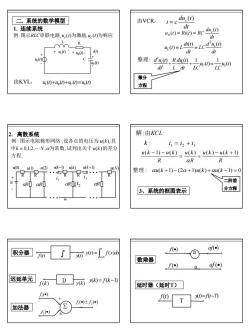
du.()二、系统的数学模型由VCR:i=dt1.连续系统ue(0)= Ri(0) = Rc 血0例:图示RLC串联电路,u,(0)为激励,u.()为响应t d=Lcd'u0ur(t)=Ldt+ 40 (0dt100整理：du@Rdu@--us(t)(0)=元d?LdtLC微分由KVL:u (t)+ur(t)+uc(t)=us(0)方程解:由KCL:2.离散系统例：图示电阻梯形网络，设各点的电压为u(k),其k:i=iz+is中k=0,1,2,.N,α为常数,试列出关于u(k)的差分u(k-1)-u(k) _ u(k) +u(k)-u(k+I)方程αRR0.re.2R?整理: cu(k+1)-(2α+1)u(k)+αu(k-1)=0中+[RTR三阶差ELCRaRti2oROR[分方程3、系统的框图表示af(o)fO)积分器0-(d7数乘器foaf()迟延单元D()=(k-1)f(k)延时器（延时T）fo(0)=f(t-1)f()Tf(0)+f.(0)加法器f全

8 二. 系统的数学模型 u (t) u (t) u (t) u (t) 由KVL： L + R + C = S L R u (t) R u (t) L u (t) S u (t) C i(t) + + + + - - - - C 1. 连续系统 例:图示RLC串联电路,us(t)为激励,uc (t)为响应 dt du t u t Ri t RC c R ( ) ( ) = ( ) = dt d u t LC dt di t u t L c L ( ) ( ) ( ) 2 = = dt du t i c c ( ) 由VCR： = ( ) 1 ( ) ( ) ( ) 1 2 2 u t LC u t dt LC du t L R dt d u t C S c c + + = 整理: 微分 方程 2. 离散系统 1i 2i 3i R αR u(N) R R αR αR u(0) u(1) u(2) E + - R R αR u(k−1) u(k) u(k+1) . . . . . 0,1,2, , , ( ) : , ( ), 方程 中 为常数 试列出关于 的差分 例 图示电阻梯形网络 设各点的电压为 其 k N u k u k = " α 解:由KCL: R u k u k R u k R u (k 1) u (k ) ( ) ( ) − ( + 1) = + − − α 整理 : αu(k +1) − (2α +1)u(k ) +αu(k −1) = 0 1 2 3 k : i = i + i 3、系统的框图表示 二阶差 分方程 迟延单元 y(k) = f (k −1) 积分器 f(t) ∫ y(t) ∫−∞ = t y(t) f (x)dx 加法器 ( ) 1f • ( ) 2f • ( ) ( ) 1 2 f • ± f • ∑ ± + f (k) Ｄ y(k) 延时器（延时T） f(t) y(t)= f(t−T) T 数乘器 f (•) af (•) a f(•) af(•) a

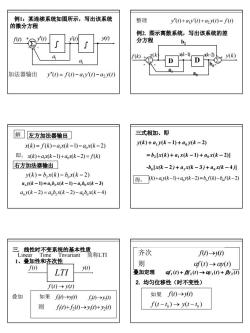
例1：某连续系统如图所示，写出该系统整理y'(t)+aiy(t)+a2y(t)= f(t)的微分方程例2.图示离散系统，写出该系统的差Jtf) 分方程0bSf(k) +DrDro加法器输出y"(t)= f(0)-aiy'(t)-a2(0)三式相加、即解左方加法器输出y(k)+ aiy(k -1)+aoy(k -2)x(k)= f(k)-a,x(k-1)-aox(k-2)即: x(k)+ax(k-1)+abx(k-2)=f(k)=bz[x(k)+ a,x(k -1)+ aox(k - 2)右方加法器输出-bo[x(k-2)+ a,x(k -3)+agx(k -4)]y(k) = b,x(k)- box(k -2)[得：(k)+a)(k-1)+a(k-2)=b,f(k)-bf(k-2)aij(k-1)=a,bzx(k-1)-a,bex(k-3)aoj(k-2)=a,b,x(k -2)-a,b,x(k-4)三、 线性时不变系统的基本性质齐次f(t)-→(t)简称LTILinelimenvariant1、叠加性和齐次性则of(t) →y(t)f(t)J(t)LTI叠加定理f.(t) + Bf2(t) →ayi(t)+ βy2(t)2.均匀位移性（时不变性）f(t)-→y(t)如果f()→0)叠加如果(0)一月0)f()→()f(t-to)→y(t-t)则fi(t)+f2(t)-→i(t)+y2(t)

9 ( ) ( ) ( ) ( ) 1 2 加法器输出 y′′ t = f t − a y′ t − a y t y′′(t) y′(t) • • f(t) + - - y(t) a1 a2 ∑ ∫ ∫ 例1：某连续系统如图所示，写出该系统 的微分方程 例2. 图示离散系统，写出该系统的差 分方程 x(k) x(k−1) x(k−2) b2 • • • f (k) + + - - - y(k) ∑ ∑ D D b0 a0 a1 ( ) ( ) ( ) ( ) 1 2 整理 y′′ t + a y′ t + a y t = f t ( ) ( ) ( 1) ( 2) x k = f k −a1x k − − a0 x k − ( ) ( ) ( 2) y k = b2 x k − b0 x k − 左方加法器输出 ( ) ( 1) ( 2) ( ) 1 0 即： x k +a x k − +a x k − = f k 右方加法器输出 ( 1) ( 1) ( 3) a1 y k − = a1b2 x k − − a1b0 x k − 解 ( 2) ( 2) ( 4) a0 y k − = a0b2 x k − − a0b0 x k − 三式相加、即 [ 2 3 4 ] 0 1 0 -b x(k − ) + a x(k − ) + a x(k − ) b [x(k) a x(k 1) a x(k 2)] = 2 + 1 − + 0 − y k a y k a y k ( ) ( 1) ( 2) + 1 − + 0 − ( ) ( 1) ( 2) ( ) ( 2) 得： y k +a1y k − +a0 y k − =b2 f k −b0 f k − f (t) y(t) LTI f (t) → y(t) 三. 线性时不变系统的基本性质 Linear Time Tnvariant 简称LTI 1、叠加性和齐次性 : ( ) ( ) 1 1 叠加 如果 f t →y t ( ) ( ) 2 2 f t →y t ( ) ( ) ( ) ( ) 1 2 1 2 则 f t + f t →y t +y t 齐次 f(t)→y(t) 则 αf (t) →αy(t) 2. 均匀位移性（时不变性） ( ) ( ) 0 0 f t − t → y t − t 如果 f(t)→y(t) ( ) ( ) ( ) ( ) 1 2 1 2 叠加定理 αf t + βf t →αy t + βy t

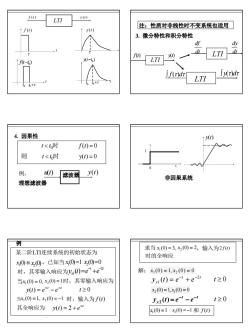
10)y(0)LTI注：性质对非线性时不变系统也适用f(0)y(t)3. 微分特性和积分特性FdfdyOLTIJ(0)(t-to)f(t-t)AIf(t)dtJy(t)dtLTIf+t4. 因果性(0)t<t时f(t)=0则t<t时y(t) =0例：ut)y(t)滤波器非因果系统理想滤波器例求当x;(0)=3,x(0)=2，输入为2()某二阶LTI连续系统的初始状态为时的全响应x(0)和(0)，已知当x(0)=1 (0)=0时，其零输入响应为yn)=e"+e"解：x(0)=1,x2(0)= 0Yx(0)= e +e-21t≥0当x(0)=0,x(0)=1时，其零输入响应为t≥0J(t) =e-t -e-x (0)=1,x(0) =0当x(0)=1, x(0)=-1 时，输入为f(0)Jx2(t)=e-t -e-rt≥0其全响应为()=2+e-(0)=1 (0)=-1 和 f()

10 f (t ) y (t ) LTI t f (t) τ t ( )0 f t−t 0t +τ 0 t t ( )0 y t−t 0t +τ 0 t y (t) τ 注：性质对非线性时不变系统也适用 3. 微分特性和积分特性 dt df LTI dt dy ∫ f(τ)dτ LTI ∫ y(τ)dτ f(t) y(t) LTI 4. 因果性 t < t0时 f (t) = 0 y( ) 0 则 t < t0时 t = 例： u(t) 滤波器 y(t) 理想滤波器 y(t) 非因果系统 1 t 0 ， 某二阶LTI连续系统的初始状态为 (0) 1x 和 (0) 2x ，已知当 x1(0)=1 , (0) 0 x2 = 时，其零输入响应为 t t x y t e e 2 1( ) − − = + t t y t e e − − ( ) = − t ≥ 0 当 (0) 0, x1 = , (0) 1 x2 = 时，其零输入响应为 当 (0) 1, x1 = , x2 (0) = −1 时，输入为 t y t e − 其全响应为 ( ) = 2 + f (t) 例 解： x1 (0) = 1, x 2 (0) = 0 t t x y t e e 2 1 ( ) − − = + t ≥ 0 求当 (0) 3, x1 = x2 (0) = 2，输入为2 f (t) 时的全响应. x2 (0) =1, x1(0) = 0 t t x y t e e − − 2 ( ) = − t ≥ 0 (0) 1 x1 ， = x2 (0) = −1 和 f (t)