《电路》课程教学资源(PPT课件)第12章 非正弦周期电流电路和信号的频谱

第十二章 非正弦周期电流电路 和信号约频谱
非正弦周期电流电路 和信号的频谱 第十二章

目录 §12.1非正弦周期信号 §12.2周期函数分解为博里叶级数 §12.3有效值、平均值和平均功率 §12.4非正弦周期电流电路的计算
目 录 §12.4 非正弦周期电流电路的计算 §12.3 有效值、平均值和平均功率 §12.1 非正弦周期信号 §12.2 周期函数分解为博里叶级数

§12.1非正弦周期信号 特点 ·不是正弦波 .按周期规律变化 f(t)=(t+kT) 非正弦周期交流信号举例:
非正弦周期交流信号举例: 特点 不是正弦波 按周期规律变化 §12.1 非正弦周期信号 f (t) = (t + kT)
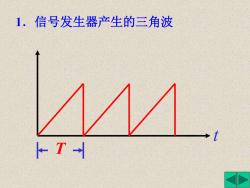
1.信号发生器产生的三角波 T
1.信号发生器产生的三角波 T t
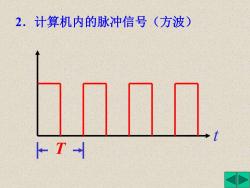
2.计算机内的脉冲信号(方波) FT-
2.计算机内的脉冲信号(方波) T t
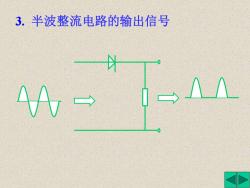
3.半波整流电路的输出信号 灯
3. 半波整流电路的输出信号

§12.2周期函数的分解 周期函数f(t)=∫(t+kT) 式中T为周期,且k=0,1,2,3. 1.傅里叶级数分解条件: 周期性 连续或只有有限个第一类 间断点(左右极限存在) 狄里赫利条件 只有有限个极值点 电工技术中的周期函数通常都能满足
§12.2 周期函数的分解 周期函数 f(t)=f(t+ kT) 式中 T为周期,且 k= 0,1,2,3··· 电工技术中的周期函数通常都能满足 1. 傅里叶级数分解条件: 狄里赫利条件 周期性 连续或只有有限个第一类 间断点(左右极限存在) 只有有限个极值点

2.周期函数f(t)如何展开成博里叶级数 f(t)=Ao 直流分量 基波(和原 十A1mc0s(Ot+W1) 函数同频) +A2mc0s(20t+V2】 二次谐波 (2倍频) 高次谐波 =A,+∑A cos((ko+,)三角级数
基波(和原 函数同频) 二次谐波 (2倍频) 直流分量 高次谐波 2. 周期函数f(t)如何展开成博里叶级数 cos( ) 三角级数 1 0 = = + + k km k A A kt + + ) + ) 2 1 2 1 1 1 0 cos(2 cos( ( ) + + = A t A t f t A m m

周期函数 f()=A。+∑dim cos(k0t+ps) 三角级数 Aim cos(kot+) A (coskotcosp-sin kotsin =Akm cosp cos kot-Aim sin or sin kot -ak coskot+b sin kot ax =Ain Cos x br=-Aim sin p f()=4,+∑a:oskot+∑b:sinkot k= k=1
= = = + + 1 1 0 k k k k f ( t) a a cos k t b sin k t 周期函数 ( ) cos( ) k k k m f t = A + A k t + = 1 0 a k t b k t A k t A k t A k t k t A k t k k km k km k km k k km k = + = − = − + cos sin cos cos sin sin (cos cos sin sin ) cos( ) k Akm k a = cos k Akm k a 0 = A0 b = − sin 三角级数

谐波分析-把一个周期函数展开或分解为具有 系列谐波的博里叶级数。 00 00 f(t)=a,+∑cosk t+∑b:sinkot k=1 k=1 a,=7f0a0)=7Jf0d0 k= 0 oko-汇k知iW 0=上ko 1 6.-子si)
= = = + + 1 1 0 k k k k f ( t) a a cos k t b sink t 谐波分析-把一个周期函数展开或分解为具有 一系列谐波的博里叶级数。 2 2 1 1 0 0 0 0 2 2 = = = = − T k T k T f t k t d t T b f t k t d t T a f t d t T f t d t T a T T ( )sin ( ) ( )cos ( ) ( ) ( ) ( ) ( ) 1 1 2 2 0 2 2 − − = = = ( )cos ( ) ( )cos ( ) ( )cos ( ) f t k t d t f t k t d t f t k t d t T T T
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电路》课程教学资源(PPT课件)第11章 三相电路.ppt
- 《电路》课程教学资源(PPT课件)第10章 含有耦合电感的电路.ppt
- 《电路》课程教学资源(PPT课件)第9章 正弦稳态电路的分析.ppt
- 《电路》课程教学资源(PPT课件)第8章 相量法.ppt
- 《电路》课程教学资源(PPT课件)第7章 二阶电路.ppt
- 《电路》课程教学资源(PPT课件)第6章 一阶电路(电路的过渡过程).ppt
- 《电路》课程教学资源(PPT课件)第5章 含有运算放大器的电阻电路.ppt
- 《电路》课程教学资源(PPT课件)第4章 电路定理(Circuit Theorems).ppt
- 《电路》课程教学资源(PPT课件)第3章 电阻电路的一般分析.ppt
- 《电路》课程教学资源(PPT课件)第2章 电阻电路的等效变换.ppt
- 《电路》课程教学资源(PPT课件)第1章 电路的基本概念和基本定律(电路模型和电路定律).ppt
- 《电路》课程教学资源(实验指导)实验20 电路矩阵方程的计算机求解.doc
- 《电路》课程教学资源(实验指导)实验19 非正弦周期信号电路的仿真.doc
- 《电路》课程教学资源(实验指导)实验18 RLC串联谐振电路的仿真.doc
- 《电路》课程教学资源(实验指导)实验17 RC一阶电路动态特性的仿真.doc
- 《电路》课程教学资源(实验指导)实验16 负阻抗变换器的制作和应用.doc
- 《电路》课程教学资源(实验指导)实验15 移相器的设计与测试.doc
- 《电路》课程教学资源(实验指导)实验10 互感与变压器.doc
- 《电路》课程教学资源(实验指导)实验14 运算放大器的应用.doc
- 《电路》课程教学资源(实验指导)实验12 二端口网络参数的测定.doc
- 《电路》课程教学资源(PPT课件)第13章 拉普拉斯变换.ppt
- 《电路》课程教学资源(PPT课件)第14章 网络函数.ppt
- 《电路》课程教学资源(PPT课件)第15章 电路方程的矩阵形式.ppt
- 《电路》课程教学资源(PPT课件)第16章 二端口网络.ppt
- 《电路》课程教学资源(PPT课件)第17章 非线性电路.ppt
- 《电路》课程教学资源(PPT课件)第18章 分布参数的电路.ppt
- 《信号与系统》课程教学大纲 Signals and Systems.pdf
- 《信号与系统》课程授课教案(课件讲稿)第3章 离散系统的时域分析.pdf
- 《信号与系统》课程授课教案(课件讲稿)第1章 信号与系统.pdf
- 《信号与系统》课程授课教案(课件讲稿)第2章 连续系统的时域分析.pdf
- 《信号与系统》课程授课教案(课件讲稿)第4章 连续系统的频域分析.pdf
- 《信号与系统》课程授课教案(课件讲稿)第7章 系统函数.pdf
- 《信号与系统》课程授课教案(课件讲稿)第5章 连续系统的S域分析.pdf
- 《信号与系统》课程授课教案(课件讲稿)第6章 离散系统的Z域变换.pdf
- 《信号与系统》课程教学课件(讲义)信号与系统实验指导书(共八个实验).pdf
- 《信号与系统》课程授课教案(课件讲稿)第8章 系统状态变量分析.pdf
- 《信号与系统》课程教学资源(习题解答)第二章 连续时间系统的时域分析.pdf
- 《信号与系统》课程教学资源(习题解答)第一章 信号与系统概述.pdf
- 《信号与系统》课程教学资源(习题解答)第三章 离散时间系统的时域分析.pdf
- 《信号与系统》课程教学资源(习题解答)第四章 连续信号的傅利叶分析.pdf
