《电路》课程教学资源（PPT课件）第10章 含有耦合电感的电路

第十章含有耦合电感的电路 9.1互感 9.2有互感的电路的计算 9.3空心变压器 9.4全耦合变压器和理想变压器

第十章 含有耦合电感的电路 9. 1 互感 9. 3空心变压器 9. 2 有互感的电路的计算 9. 4 全耦合变压器和理想变压器 `

9.1互感和互感电压 一、互感和互感电压 N .21 当线圈1中通入电流，时，在线圈1中产生磁通(nagnetic flux), 同时，有部分磁通穿过临近线圈2。当为时变电流时，磁通也将 随时间变化，从而在线圈两端产生感应电压。 更1=Φ21+更1 i1,N1→平=N1D1L1=i1 总磁通想醛》 漏磁通 中21在线圈N2产生磁链！ 平1=N2④21 定义：M1= 21 为线圈1对2的互感系数，单位亨（田 (mutual inductance coefficient) 当i1、41、山21方向与Φ符合右手定则时，根据电磁感应定律： d4= d 21= dΨ21=M21 di 41:自感电压； dt dt dt dt 山21：互感电压

9. 1 互感和互感电压 一、 互感和互感电压 + u11 – + u21 –  21 i1 N1 N2 当线圈1中通入电流i1时，在线圈1中产生磁通(magnetic flux)， 同时，有部分磁通穿过临近线圈2。当i1为时变电流时，磁通也将 随时间变化，从而在线圈两端产生感应电压。 s1 i1，N1→ Y11= N111 L1=Y11/i1 总磁通 21在线圈N2 产生磁链 Y21= N221 耦合磁通 漏磁通 （主磁通） 11 = 21 + s1 定义： 为线圈1对2的互感系数，单位亨 (H) 1 21 21 i M  = (mutual inductance coefficient) 11 当i1、u11、u21方向与 符合右手定则时，根据电磁感应定律: d d d d 1 1 11 11 t i L t u = Y = t i M t u d d d d 1 21 21 21 = Y = u11：自感电压； u21：互感电压

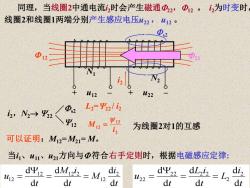
同理，当线圈2中通电流时会产生磁通④2，④12。，为时变时 线圈2和线圈1两端分别产生感应电压422,412· W12 W22 L2=Y2/i2 2,N2→2 /①2 Y12 M2=2 为线圈2对1的互感 可以证明：M12=M21=M。 当1、411、21方向与Φ符合右手定则时，根据电磁感应定律： dM dt z 22= dΨ22=9 dt dt dt =L dt dt

可以证明：M12= M21= M。 同理，当线圈2中通电流i2时会产生磁通22，12 。 i2为时变时， 线圈2和线圈1两端分别产生感应电压u22 ， u12 。 d d d d d d 2 2 2 2 2 2 2 2 t i L t L i t u = = Y = t i M t M i t u d d d d d d 2 1 2 1 2 1 2 2 1 2 = = Y = 2 12 12 i M  = 为线圈2对1的互感 i2，N2→ Y22 s2 Y12 L2=Y22 / i2 + u12 – + u22 – i2  12 N1 N2 s2 22 当i1、u11、u21方向与 符合右手定则时，根据电磁感应定律:

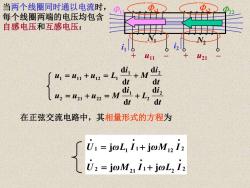
当两个线圈同时通以电流时， ①1 每个线圈两端的电压均包含 自感电压和互感电压： 11 W21 ∫=4+“：=4 M. dt iz 题=业+EM验+凸G 在正弦交流电路中，其相量形式的方程为 「U1=jwL,i1+jwM2i2 U2=joMaI1+j@L2I2

当两个线圈同时通以电流时， 每个线圈两端的电压均包含 自感电压和互感电压： t i L t i u u u M t i M t i u u u L d d d d d d d d 2 2 1 2 2 1 2 2 1 2 1 1 1 1 2 1 = + = + = + = + 在正弦交流电路中，其相量形式的方程为 2 2 1 21 2 2 12 1 1 1 j j j j • • • • • • = + = + U ωM I ωL I U ωL I ωM I + u11 – + u21 – i1 N1 N2  s1 11 s2 i2 22

1.互感的性质 ①从能量角度可以证明，对于线性电感M12=M1=M ②互感系数M只与两个线圈的几何尺寸、匝数、相互位置 和周围的介质磁导率有关，如其他条件不变时，有 Mo N N2 (Lo N2) 2.耦合系数(coupling coefficient)k: k表示两个线圈磁耦合的紧密程度。 M 可以证明，≤1。 VLL2 全耦合：D、1=①20 即④11=④21，④22=④12 :h=N9,h-N,0,M1-N,M。-V@ i .Mi2M2=LL2 M2=LL .k=1

2.耦合系数 (coupling coefficient) k： k 表示两个线圈磁耦合的紧密程度。 全耦合:  s1 =s2=0 1 2 def L L k = M 即 11= 21 ， 22 =12 , 1 , , , 1 2 2 1 2 2 1 1 2 2 1 1 2 1 2 1 2 2 1 2 1 2 2 2 2 2 1 1 1 1 1  = =  = = = = = M M L L M L L k i N Φ M i N Φ M i N Φ L i N Φ  L 可以证明，k1。 1. 互感的性质 ①从能量角度可以证明，对于线性电感 M12=M21=M ②互感系数M 只与两个线圈的几何尺寸、匝数 、 相互位置 和周围的介质磁导率有关，如其他条件不变时，有 M  N1N2 （L  N2）

3.互感线圈的同名端 具有互感的线圈两端的电压包含自感电压和互感电 压。表达式的符号与参考方向和线圈绕向有关。对自感 电压，当山，i取关联参考方向，与Φ符合右螺旋定则， 其表达式为 =N验= 41= dt 上式说明，对于自感电压由于电压电流为同一线圈上的， 只要参考方向确定了，其数学描述便可容易地写出，可不用 考虑线圈绕向。对线性电感，用山，描述其特性，当山，取关联 方向时，符号为正；当山，为非关联方向时，符号为负

3. 互感线圈的同名端 具有互感的线圈两端的电压包含自感电压和互感电 压。表达式的符号与参考方向和线圈绕向有关。对自感 电压，当u, i 取关联参考方向，i与 符合右螺旋定则， 其表达式为 d d d d d d 1 1 11 1 11 11 t i L t Φ N t Ψ u = = = 上式说明，对于自感电压由于电压电流为同一线圈上的， 只要参考方向确定了，其数学描述便可容易地写出，可不用 考虑线圈绕向。对线性电感，用u,i描述其特性，当u,i取关联 方向时，符号为正；当u,i为非关联方向时，符号为负

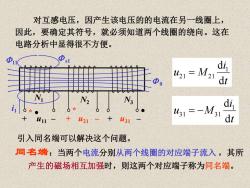
对互感电压，因产生该电压的的电流在另一线圈上， 因此，要确定其符号，就必须知道两个线圈的绕向。这在 电路分析中显得很不方便。 421=M21 di dr 431=-M31 di 421 u31 dt 引入同名端可以解决这个问题。 同名端：当两个电流分别从两个线圈的对应端子流入，其所 产生的磁场相互加强时，则这两个对应端子称为同名端

对互感电压，因产生该电压的的电流在另一线圈上， 因此，要确定其符号，就必须知道两个线圈的绕向。这在 电路分析中显得很不方便。 + u11 – + u21 – i1 11  0 N1 N2 + u31 – N3  s1 t i u M d d 1 21 = 21 引入同名端可以解决这个问题。 同名端：当两个电流分别从两个线圈的对应端子流入 ，其所 产生的磁场相互加强时，则这两个对应端子称为同名端。 * • * • t i u M d d 1 31 = − 31

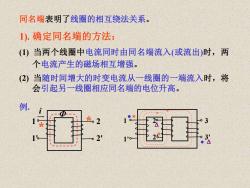
同名端表明了线圈的相互绕法关系。 1).确定同名端的方法： ()当两个线圈中电流同时由同名端流入（或流出）时，两 个电流产生的磁场相互增强。 (②)当随时间增大的时变电流从一线圈的一端流入时，将 会引起另一线圈相应同名端的电位升高。 例。 必。2 2 3

同名端表明了线圈的相互绕法关系。 1). 确定同名端的方法： (1) 当两个线圈中电流同时由同名端流入(或流出)时，两 个电流产生的磁场相互增强。 (2) 当随时间增大的时变电流从一线圈的一端流入时，将 会引起另一线圈相应同名端的电位升高。 i  1 1' 2 2' * * 1 1' 2 2' 3' 3 * * • •   例

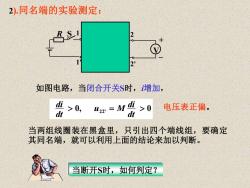
2)同名端的实验测定： 如图电路，当闭合开关$时，增加， 盟>0 4x=M出 >0 电压表正偏。 当两组线圈装在黑盒里，只引出四个端线组，要确定 其同名端，就可以利用上面的结论来加以判断。 当断开$时，如何判定？

2).同名端的实验测定： i 1 1' 2 2' * * R S V + –  0, 2 2' =  0 电压表正偏。 dt M di u dt di 如图电路，当闭合开关S时，i增加， 当两组线圈装在黑盒里，只引出四个端线组，要确定 其同名端，就可以利用上面的结论来加以判断。 当断开S时，如何判定？

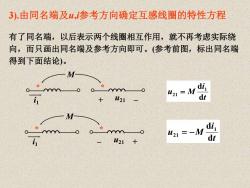
3).由同名端及山，参考方向确定互感线圈的特性方程 有了同名端，以后表示两个线圈相互作用，就不再考虑实际绕 向，而只画出同名端及参考方向即可。（参考前图，标出同名端 得到下面结论)。 M- *m0 41=M i 21 dt m 421=-M di, dt

3).由同名端及u,i参考方向确定互感线圈的特性方程 有了同名端，以后表示两个线圈相互作用，就不再考虑实际绕 向，而只画出同名端及参考方向即可。(参考前图，标出同名端 得到下面结论)。 t i u M d d 1 21 = t i u M d d 1 21 = − i1 * * + u21 – M i1 * * – u21 + M