《信号与系统》课程授课教案（课件讲稿）第2章 连续系统的时域分析

第二章连续系统的时域分析经典法：本章在用经典法求解微分方程1.微分方程的建立的基础上，讨论零输入响应、零状①根据KCL、KVL、VCR列出相应方程态响应的求解。在引入系统的冲激响应后，零状态响应等于冲激响应②根据待求变量化简方程与激励的卷积积分。2.微分方程的求解全解=齐次解+特解$2-1LTI连续系统的响应或缩写：，微分方程的经典解-单输入一单输出系统dtiadn阶常系数线性微分方程全解(t)=y,(t)+y,()d"y+and'y()+aoy)+ada.d"drt[oat当入为m重根①齐次解y,(l)d"y+alddr+()=0-20n+dya,Zc,e4dt"dt1=1i=m+1特征方程"+an-1an-+...+aa+ao=0b.复根a.实根对共轭复根=α+β=α-jβn个实根A1,12,... Nn:分量 :e[C cos(βt)+ Dsin(βt)]y(t) =

1 信号与系统电子课件 第二章 连续系统的时域分析 本章在用经典法求解微分方程 的基础上，讨论零输入响应、零状 态响应的求解。在引入系统的冲激 响应后，零状态响应等于冲激响应 与激励的卷积积分。 信号与系统电子课件 1. 微分方程的建立 ①根据KCL、KVL、VCR列出相应方程 ②根据待求变量化简方程 2. 微分方程的求解 全解=齐次解+特解 经典法： 信号与系统电子课件 §2-1 LTI连续系统的响应 一. 微分方程的经典解 单输入—单输出系统 n阶常系数线性微分方程 ( ) ( ) ( ) ( ) 1 1 0 1 1 a y t dt dy t a dt d y t a dt d y t a n n n n n n + + + + − − − " ( ) ( ) ( ) ( ) 1 1 0 1 1 b f t dt df t b dt d f t b dt d f t b m m m m m = m + + + + − − − " 信号与系统电子课件 或缩写： y(t) y (t) y (t) 全解 = h + p j m j j j i n i i i dt d f t b dt d y t a ( ) ( ) 0 0 ∑ ∑ = = = 信号与系统电子课件 y (t) ①齐次解 h ( ) 0 ( ) ( ) ( ) 1 1 0 1 + 1 + + + = − − − a y t dt dy t a dt d y t a dt d y t n n n n n " : 0 1 0 1 + 1 + + + = − − a a a n n n 特征方程 λ λ " λ n个实根 λ 1, λ 2 ," λ n : a. 实根 ∑= = n i t i i y t C e 1 ( ) λ 信号与系统电子课件 当λ为m重根 t n i m i m i t m i h i i y t c t e c e λ λ ∑ ∑= + − = = + 1 1 ( ) b. 复根 : e [C cos( t) Dsin( t)] t β β α 分量 + 一对共轭复根 λ1 = α + jβ λ2 = α − jβ

C.正弦激励f(t)= Em sin(ot+Φ)②特解y,(t)y,(t)= Asinot + Bcosot特解的函数形式与激励函数的形式有关其中cejw=A+jB=C sin(ot+y)a.常数激励f(t）=Ey,()=Ad、tmb.指数激励f(t) = Eeaαkyp(t)= Am" + Am-1"- +.+A++Ay,(t)= Aear③全解例：描述某LTI系统的微分方程为a. 通解-齐次通解+非齐次特解4%+60-10y(t) = yh(t)+ yp(t)dtZc,ea" + y,(t)试求当/()=2e,≥0,(0)=2,(0)=-1时的全解解：特征方程2+51+6=0b.定解：给定初始条件特征根=-2,=-3(0)、y)(0)、y(2) (0).y(-1)(0)齐次通解Yh(1)=C,e-21 +C,e-3代入通解，确定系数 ck特解设yp(t)= Ae-代入方程Ae-1 + 5(-Ae-")+6Ae-l =2e-y(t) = 3e-21 - 2e-3t + e-t≥0A=1p(t) = e-I自由响应强迫响应通解(t) = Ce-21 +Ce-31 +e-i由(0)=2, y(0)=-1r1+C,+C, = 2L-1- 2C, -3C, =-1得Ci =3, C2 = -2

2 信号与系统电子课件 yp(t) = A t y p t Aeα ( ) = 特解的函数形式与激励函数的形式有关 a. 常数激励 f (t ) = E K t f t Ee α λ α b. 指数激励 ( ) = ≠ y (t) ②特解 p 信号与系统电子课件 y t A t B t p ( ) = sinω + cosω = C t + c = A + jB ψ ω ψ j sin( ) 其中 e f (t) = E sin(ωt + φ ) m c. 正弦激励 ③全解 1 0 1 1 y (t) A t A t A t A m m m p = m + + + + − − " d、 m t 信号与系统电子课件 y (t ) y (t ) y (t ) = h + p a. 通解=齐次通解+非齐次特解 ( ) 1 C e y t p t n i i i = ∑ + = λ b. 定解：给定初始条件 k 代入通解 ,确定糸数 c (0) (0) (0) (0) (1) (2) (n−1) y 、y 、y 、"y 信号与系统电子课件 : 5 6 0 2 解 特征方程 λ + λ + = 特征根 λ1 = −2, λ2 = −3 t t h y t C e C e 3 2 2 1 ( ) − − 齐次通解 = + t yp t Ae− 特解 设 ( ) = 5 6 ( ) ( ) 2 2 y t f t dt dy dt d y + + = 试求当f (t) = 2e−t ,t ≥ 0; y(0) = 2, y′(0) = −1时的全解 例：描述某LTI系统的微分方程为 信号与系统电子课件 t t t t Ae Ae Ae e − − − − 代入方程 + 5(− ) + 6 = 2 A = 1 t p y t e − ( ) = t t t y t C e C e e − − − = + + 3 2 2 1 通解 ( ) 由y(0) = 2, y′(0) = −1 1 2 3 1 1 2 1 2 1 2 − − − = − + + = C C C C 3, 2 得 C1 = C2 = − 信号与系统电子课件 ( ) 3 2 , 0 2 3 = − + ≥ − − − y t e e e t t t t 自由响应 强迫响应

初始条件的求法如((0.)→((0.）二0_与0初始值例：描述某LTI系统的微分方程.定义0y'(t)+3y(t)+2y(t)=2 f'()+6f (t)00+2. 初始条件已知y(0_)=2,y(0)=0, ()=u(1),求 y(0.)和 y(0.)解：分析0_激励作用前的状态a由于函数的引入，(0)y(0.）如(0_), y)(0.)b.由于激励的加入,在微分方程右端出现了ot激励作用后一瞬间的状态AS(t),Bo(t)等,则方程左端也应有对应如(04),y (0 )相等的冲激函数项从0_到0，两端进行积分将(t)=u(t)代入方程y'(t)+3y(t)+2y()=28(0)+6u(t)[y(t)d +3f y(0)dt+2 v()dt=2 8(0dt +6J u(0)d0.1则j"(t)=A8(t)（连续）2×1y'(t) = Au(t)y'(0+)+ y'(0_)(t) = Ar(t)于是[y(0.)-y(0_)]+3[(0)- (0_)]=2由于y(t)连续y(0.)=y(0_)=2y(0)= 2+ y(0.)=2y'(0.)= 2 + y(0_)=2总结y'(t)+3y'(t)+2y(t)= J (0)当f()= 0, A,ea , sin otp(-ce +)-y合(0.)*y0(.当()含8(1)或8 ()

3 信号与系统电子课件 0− 0 0+ 0− 激励作用前的状态 二.0−与0+初始值 1. 定义 2. 初始条件 (0 ), (0 ) ( ) − − j 如y y 0+ 激励作用后一瞬间的状态 (0 ), (0 ) ( ) + + j 如y y 信号与系统电子课件 初始条件的求法: (0 ) (0 ) ( ) ( ) − → + j j 如y y y (t) 3 y (t) 2 y(t) 2 f (t) + 6 f (t) ′′ + ′ + = ′ (0 ) 2, (0 ) 0, ( ) ( ), (0 ) (0 ) − − + + 巳知y = y′ = f t = u t 求 y 和 y′ 例：描述某LTI系统的微分方程 解： a 由于δ函数的引入， (0 ) (0 ) ( ) ( ) − ≠ + j j y y , ( ) , . , B t b δ ′ Aδ (t) 相等的冲激函数项 等 则方程左端也应有对应 由于激励的加入 在微分方程右端出现了 分析 信号与系统电子课件 y′′(t) +3y′(t) + 2y(t) = 2δ (t) + 6u(t) 将f (t) = u(t)代入方程 则 y"(t) = Aδ (t) '( ) ( ) '(0 ) '(0 ) = + ≠ − y t Au t y y 信号与系统电子课件 ∫ ∫ ∫ ∫ ∫ + − + − + − + − + − ′′ + ′ + = + 0 0 0 0 0 0 0 0 0 0 y (t)dt 3 y (t)dt 2 y(t)dt 2 δ (t)dt 6 u(t)dt 从0−到0+两端进行积分 − 于是 [y′(0+ )− y′(0−)]+3[y (0+)− y (0−)]= 2 ( ) (0 ) = (0 ) = 2 + − 由于y t 连续 y y 2×1 0 0 ∵ y(t) = Ar(t) 连续 信号与系统电子课件 y′(0+ ) = 2 + y′(0− ) = 2 总结 y′′(t) + 3 y′(t) + 2 y(t) = f (t) f ( )t A e t t ω α 当 = 0 , , , sin ( ) ( ) 1 y t C e y t p t n i i i = ∑ + = λ (0 ) (0 ) ( ) ( ) − = + j j y y 当f ( )t 含δ (t)或δ '(t) (0 ) (0 ) ( ) ( ) − ≠ + j j y y 信号与系统电子课件 y′(0+ ) = 2 + y′(0− ) = 2

三.零输入响应和零状态响应③全响应的两种分解形式y(t) = y+(t)+ yr(t)①零输入响应ZChen+ZChe'* +y,()特征根为单根yr(t)=ZCe4i=l=l②零状态响应零输入响应零状态响应特征根为单根-Zc,e +y,(t)y(t)=Zcher +y,(t)1=1=1自由响应强迫响应y ( (0. )= y0)(0. )c,e'Cme+Cher显然=由于激励为零1-1y((0. )=y((0. )= y0(0. )④初始值的分解()=y()+y()例：描述某LTI系统的微分方程设t=0(0.)=y(0.)+y (0)({) + 2y'(t) + 2y() = f()t=0+(0)=y(0)+y0(0)已知(0_)=0, y(0_)=1,f()=8(1),求零输入响应和零状态响应t=0接入激励，则y("(0.)=0代入初始值，得解：(1)求零输入响应y(t)yr(0+)=C= 0y"()+2y()+2y()=0y'(0+)= -C +C2 = 1【且满足y(0+),(0.)解得C,=0，C2=1y.(0.)=y.(0_)=y(0. )=0t≥0yr(t)=e' sinty(0+)= y* (0. )= y(0.)=1(2)求零状态响应y,()特征根A12 = -1± j[y'r(t)+2y 'r(t)+2y ,(t) =8()( y,(0.)= yr(0.)=0y,(t)=(C cost+Cr sint)e-

4 信号与系统电子课件 三.零输入响应和零状态响应 ①零输入响应: 特征根为单根 ∑= = n i t x xi i y t C e 1 ( ) λ ②零状态响应: 特征根为单根 ∑= = n i t f fi i y t C e 1 ( ) λ y (t) + p 信号与系统电子课件 y (t) y (t) y (t) = x + f ③全响应的两种分解形式 自由响应 强迫响应 零输入响应 零状态响应 ( ) 1 C e y t p n i t i i = ∑ + = λ ( ) 1 1 C e C e y t p n i t fi n i t xi i i = ∑ +∑ + = = λ λ 信号与系统电子课件 ∑ ∑ ∑ = = = = + n i t fi n i t xi n i t i i i i C e C e C e 1 1 1 λ λ λ 显然 ④初始值的分解 t 0 (0 ) (0 ) (0 ) ( ) ( ) ( ) = + + = + + + f j x j j y y y () () () ( ) ( ) ( ) y t y t y f t j x j j = + t 0 , (0 ) 0 - ( ) = = j f 接入激励 则 y () () () t 0 (0 ) (0 ) (0 ) jj j x f yy y 设 = =+ − −−− 信号与系统电子课件 (0 ) (0 ) ( ) ( ) − = − j j x y y (0 ) (0 ) (0 ) ( ) ( ) ( ) + = − = − j j x j x y y y 由于激励为零 例：描述某LTI系统的微分方程 求零输入响应和零状态 响应 已知 (0 ) 0, (0 ) 1, ( ) ( ), ' y = y = f t = ε t − − y"(t) + 2 y'(t) + 2 y(t) = f'(t) 信号与系统电子课件 解: (1) y (t) 求零输入响应 x y" x(t) + 2 y' x(t) + 2 y x(t) = 0 (0 ), ' (0 ) x + x + 且满足 y y ' (0 ) ' (0 ) '(0 ) 1 (0 ) (0 ) (0 ) 0 = = = = = = + − − + − − y y y y y y x x ∵ x x = − 1 ± j 特征根 λ 1,2 t x x x y C t C t e− ∴ (t ) = ( cos + sin ) 1 2 信号与系统电子课件 ' (0 ) 1 (0 ) 0 1 2 1 = − + = = = + + x x x x x y C C y C 代入初始值，得 解得Cx1 = 0，Cx 2 = 1 ∴ (t ) = sin t ≥ 0 − y e t t x (2) y (t) 求零状态响应 f y (t) 2y (t) 2y (t) ( ) " ' t f f + f + = δ y (0 ) y (0 ) 0 - ' f - = f =

(0 )=1-yf(0_)=1从0求0则y r (t)含8(t),yr(t)含u(t);t>0时，方程为y(0.)yr(0_),y,()连续y r(t)+2y'r(t)+2y,(t) = 0从0_到0.两端进行积分通解 y,(t)=(Cni cost+Cr2 sint)e-[y,"(t)dt +2 jyr'(0)dt +2 y,(n)dt= jo(t)dt代入初始值,(0,)=Cn=0[(0+)-(0_]+2(0)-y(0.)]=1yr(0+)=-Cn +Cr2 =1r(0+)=r(0.)=0$ 2-3系统的阶跃响应和冲激响应解之Cr= 0,Cf2 =1阶跃响应y,(t) = sin te-t初始状态为零时,由单位阶跃函数所引起的响应f()=u(t),系统的微分方程为d"gl)+an-d(ag( +.+ aog()= (0)dtndtn-lg()(0_)=0, j= 0,1,2, ..n-1二。 冲激响应由于g"(t)含ε(t)初始状态为零时，由单位冲激函数s(1)所引则 g(0.)= g(0_)=0, j=0,1,2,..n起的响应1. 冲激响应的特点1)s(t)rg(t)=(Z cie +ucs(t)ea08(1)=0,t# 01 g(0)-= .-)(0.)=0L8(1) = 00, = 0其中六为特解u.(0_)=0-→u.(0)=Ut>0时本质上是零输入响应

5 信号与系统电子课件 从0−到0+两端进行积分 连续 则 含 含 (0 ) (0 ); ( ) ( ) ( ), ( ) ( ); ' ' " ' y y y t y t t y t u t f f f f f + ≠ − 从0-求0+ δ ∫ ∫ ∫ ∫ + + + + + + = 0 0 0 0 0 0 0 0- - - - y "(t)dt 2 y '(t)dt 2 y (t)dt (t)dt f f f δ [ y' ( 0 )-y' (0 )] 2[ y (0 )-y ( 0 )] 1 ∴ f + f − + f + f - = y ( ) y ( ) f 0 + = f 0- = 0 =0 信号与系统电子课件 0 = 1− 0 = 1 + − y' ( ) y' ( ) f f y (t) 2y (t) 2y (t) 0 t 0 " ' + + = > f f f 时，方程为 t f f f C t C t e − y (t) = ( cos + sin ) 通解 1 2 y '(0 ) - 1 y (0 ) 0 1 2 1 = + = = = + + f f f f f C C 代入初始值 C 信号与系统电子课件 0 1 解之 Cf 1 = , Cf 2 = y t te t f − ( ) = sin 信号与系统电子课件 §2-3 系统的阶跃响应和冲激响应 f (t) = u(t),系统的微分方程为 ( ) ( ) ( ) ( ) 1 0 ( 1) 1 a g t t dt d g t a dt d g t a n n n n n n + + + = ε − − − " (0 ) 0, 0,1,2, 1 ( ) g − = j = n − j " 一. 阶跃响应 初始状态为零时,由单位阶跃函数所引 起的响应 信号与系统电子课件 g (t) (t) n 由于 含ε (0 ) (0 ) 0, 0,1,2, 1 ( ) ( ) g + = g − = j = n − 则 j j " ) ( ) 1 ( ) ( 1 0 t a g t C e t n i i i ε λ = ∑ + = (0 ) (0 ) 0 ( 1) = = + = − + n g " g 其中 为特解 0 1 a 信号与系统电子课件 ( ) , 0 ( ) 0, 0 = ∞ = = ≠ t t t t δ δ 二. 冲激响应 1. 冲激响应的特点 uc (0− ) = 0 →uc (0+ ) =U 初始状态为零时, 由单位冲激函数 所引 起的响应 δ (t) C R + - u δ (t) c 0 时本质上是零输入响应. > + t

因此,冲激响应与零输入响应具有代入方程，平衡系数相同的函数形式C=B-AT,D=A2. 一阶系统的冲激响应h(t)=(B - AT)e-" e(0)+ A8(0)dhO +Th(0)= 4d& + B83. 线性系统的冲激响应ddtd"h)+..a?dh(t) + agh(t)分析 h(t)有 ce - (t)项,amdtndt设h(1)= Ce -" g(0)+ D(l)d"&.+Ad8+A8为平衡两边一=Am dtm应有6(1)项de(t)由定义 e()=[a(t)dtam<n8(t) =dth(0) = (Zc,e ")e(0)根据LTI系统的微（积）分特性-1dg(l)b.m=ng(1)= [ h(t)dth(t)=dth(0)=(2C,e)e(0) +D8(0)例：设描述二阶LTI系统的微分方程为C、D待定系数，通过比较系数得出+5+6y=j0)4.冲激响应与阶跃响应的关系求其冲激响应和阶跃响应由奇异函数平衡：h"(t)含8(t)→h't)含ε(t),解：①冲激响应h(0)+h(0.h(t)连续y(t)= h(t)由定义J(0)=00)时从0到0.积分d h(0) +5 dh( +6h(0)=8(0)[h(0,)-h(0.)])+5[h(0.)-h(0_]+6 h(0)dt- j8(0)ddt?dt- h(0.)=h(0.)=0[s(t)dt = 1,: J h(t)dt=0特征根：M= -2, /2=-3h(t)=(cie-21 + C2e-3r)e(t)h(0.)= h(0.)=0

6 信号与系统电子课件 δ δ B dt d Th t A dt dh t + ( ) = + ( ) h (t) Ce (t) D (t) Tt = ε + δ 设 − 因此, 冲激响应与零输入响应具有 相同的函数形式 2. 一阶系统的冲激响应 h (t )有 ce (t )项 , Tt ε 分析 − 应有 项 为平衡两边 ( ) , δ t 信号与系统电子课件 C = B − AT, D = A h(t) (B AT )e (t) A (t) Tt = − ε + δ − 代入方程, 平衡系数 ( ) ( ) ( ) 1 0 a h t dt dh t a dt d h t a n n m + " + + 3. 线性系统的冲激响应 δ δ δ A dt d A dt d A m m = m + "+ 1 + 信号与系统电子课件 ( ) ( ) ( ) 1 h t C e t t n i i i ε λ ∑= = b.m=n Ci 、D待定系数, 通过比较系数得出 4. 冲激响应与阶跃响应的关系 + Dδ (t) a.m<n ( ) ( ) ( ) 1 h t C e t t n i i i ε λ ∑= = 信号与系统电子课件 ∫ −∞ = t 由定义: ε(t) δ(τ)dτ dt d t t ( ) ( ) ε δ = 根据LTI系统的微（积）分特性 dt dg t h t ( ) ∫ ( ) = −∞ = t g (t) h(τ )dτ 5 6 ( ) 2 2 y f t dt dy dt d y + + = 例：设描述二阶LTI系统的微分方程为 求其冲激响应和阶跃响应 信号与系统电子课件 :由定义 f(t)=δ(t)时, y(t) = h(t) 6 ( ) ( ) ( ) 5 ( ) 2 2 h t t dt dh t dt d h t + + = δ h′(0− ) = h(0− ) = 0 : 2, 3 1 2 特征根 λ = − λ = − ( ) ( ) ( ) 3 2 2 1 h t c e c e t t t ε − − = + 解： ①冲激响应 信号与系统电子课件 (0 ) (0 )→ h(t)连续 : ( ) ( ) ( ) ( ), + − ′ ≠ ′ ′′ → ′ h h 由奇异函数平衡 h t 含δ t h t 含ε t ∫ ∫ + − + − ′ + ′ − + + − + = 0 0 0 0 [h (0 )- h (0 )] 5[h(0 )- h(0 )] 6 h(t)dt δ (t)dt 从0+到0- 积分 ( ) 0 0 0 = ∫ + − ∵ h t dt ( ) 1, 0 0 = ∫ + − δ t dt (0 ) = (0 ) = 0 + − h h

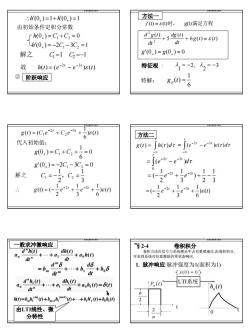
方法一..h(0.)=1+h(0.)=1f(t)=(t)时,g(t)满足方程由初始条件定积分常数d'g(t) + dg(t)+rh(0,)=C,+C, =0+6g(t)=ε(t)dt?dtLh(0)=-2C,-3C, =1g(0_)= g(0_)=0解之G=1 C=-1特征根 =-2, 元, =-3故 h(t) =(e-21 - e-3)e(1)1②阶跃响应特解：g,(0)=g(t)=(Cje-21 +Cze-3+6(0)方法二代入初始值：[(e--2r -e-3r )e(t)dt[h(t)dt:g(t) ==0g(0.)=C +C, +J(e- -e")dtg(0.)=-2C, -3C, =0-21解之-31)+C,=--,,C2=323231e-"+e-21-)e(t)10-2110-3g(t) =(-2+)e(t)=（一般求冲激响应*$2-4卷积积分dho..a,dtdh() + agh(t)差积方法在信号与占有重要地位,由卷积积分，an可求得系统对任意激励的零状态响应dt"d"sd8+b81.脉冲响应:脉冲强度为1(面积为1)+.bdt=h(x(0) = 0)dtmd"h(t)+.+a.LTI系统() + aoh ()=8()P,(0)h,(t)dtdf0)=bh(m()+bu((++b (0+bh()由LTI线性、微2分特性

7 信号与系统电子课件 ∴h′(0+ ) =1+ h′(0− ) =1 由初始条件定积分常数 (0 ) 2 3 1 (0 ) 0 1 2 1 2 ′ = − − = = + = + + h C C h C C 解之 C1 =1 C2 =−1 ( ) ( ) ( ) 2 3 h t e e t t t ε − − 故 = − ② 阶跃响应 信号与系统电子课件 f (t) = ε (t)时， g(t)满足方程 6 ( ) ( ) ( ) 5 ( ) 2 2 g t t dt dg t dt d g t + + = ε '(0 ) = (0 ) = 0 − − g g : 2, 3 1 2 特征根 λ = − λ = − 特解： 6 1 g p (t) = 方法一 信号与系统电子课件 ) ( ) 6 1 ( ) ( 3 2 2 1 g t C e C e t t t = + + ε − − 代入初始值： '(0 ) 2 3 0 0 6 1 (0 ) 1 2 1 2 = − − = = + + = + + g C C g C C 3 1 2 1 解之 C1 = − ，C2 = ) ( ) 6 1 3 1 2 1 (t) ( 2 3 g e e t t t ∴ = − + + ε − − 信号与系统电子课件 方法二 ∫ −∞ = t g (t) h(τ )dτ ε τ τ τ τ e e d t ( ) ( ) 2 3 ∫ −∞ − − = − τ τ τ e e d t ∫ − − = − 0 2 3 ( ) 3 1 2 1 ) 3 1 2 1 ( 2 3 = − + + − − t − t e e ) ( ) 6 1 3 1 2 1 ( 2 3 e e t t t = − + + ε − − 信号与系统电子课件 一般求冲激响应 ( ) ( ) ( ) ( ) 0 1 1 1 1 a h t t dt dh t a dt d h t a n n n +"+ + = δ 由LTI线性、微 分特性 ( ) ( ) ( ) ' ( ) ( ) 1 1 0 1 ( 1) 1 1 ( ) 1 h t b h t b h t b h t b h t m m m = m + + + + − − " ( ) ( ) ( ) 1 0 a h t dt dh t a dt d h t a n n n + " + + δ δ δ 1 b0 dt d b dt d b m m = m + "+ + 信号与系统电子课件 卷积方法在信号与系统理论中占有重要地位,由卷积积分, 可求得系统对任意激励的零状态响应. 1. 脉冲响应:脉冲强度为1(面积为1) P (t) n 2 n n 2 t h (t) n t 0 x (0 ) = 0 LTI系统 §2-4 卷积积分

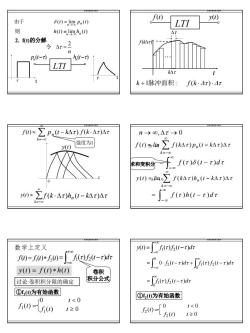
f(t)y(t)由于8(t) = lim P,(0)LTI则h(t)=limh,(t)At2. f(t)的分解f(kAt)tAT:h(t-t)p(t-LTIkAtk+1脉冲面积：f(k.At).At8J()~Zp,(t-kt) f(k.At)Atn00,4t0k=-0强度为()(kAT)P(-AT)Ary(t)f(t)s(t-t)dt求和变积分y(t)=linoZ (kAt)h,(t-kAt)Atk=-0(0)~ f(k.At)h,(t-kAt)Atf(t)h(t-t)dt数学上定义y(t)=/fi(t)f(t-t)dtfi(t)f2(t-t)dtf(0)=f(0)*f:()=° 0.(t-t)dt+[(t)(t-)dty(t) = f(t)* h(t)卷积积分公式[fi(t)f2(t-t)dt讨论：卷积积分限的确定①r,(t)为有始函数①f,()为有始函数t<0Ufi()=L()t<0t≥0z(t)=2(t)t≥0

8 信号与系统电子课件 h(t) lim h (t) 则 =n → ∞ n (t) lim p (t) 由于 δ = n n → ∞ p (t−τ) n LTI h (t−τ) n n 2 令 ∆τ = τ t 2. f(t)的分解 τ t 信号与系统电子课件 f (t) LTI y(t) f (k∆τ) t k∆τ ∆τ " k +1脉冲面积 : f (k ⋅∆τ )⋅∆τ 信号与系统电子课件 ∑ ∞ =−∞ ≈ k f (t) ∑ ∞ =−∞ ≈ k y(t) 0 t y(t) p (t − k∆τ ) n f (k ⋅∆τ )h (t − k∆τ )∆τ n 强度为1 f (k ⋅∆τ )∆τ 信号与系统电子课件 = f (τ )δ (t − τ )dτ ∫ ∞ − ∞ = ∑ ∆τ − ∆τ ∆τ ∞ =−∞ f (t) lin f (k ) p (t k ) n k ∆τ →0 = ∑ ∆τ − ∆τ ∆τ ∞ = −∞ y (t) lin f (k )h (t k ) n k = f (τ )h (t − τ )d τ ∫ ∞ − ∞ ∆τ → 0 n → ∞,∆τ → 0 求和变积分 信号与系统电子课件 ( ) ( ) ( ) 1 2 f t = f t ∗ f t 数学上定义 f (τ)f (t τ)dτ = 1 2 − ∫ +∞ −∞ y(t) = f (t) ∗ h(t) ①f1(t)为有始函数 f1(t) = ( ) 0 0 0 1 ≥ < f t t t 讨论:卷积积分限的确定 卷积 积分公式 信号与系统电子课件 y(t) f (τ ) f (t τ )dτ = 1 2 − ∫ +∞ −∞ 0 f (t τ )dτ f (τ ) f (t τ )dτ 2 0 1 0 = ⋅ 2 − + − ∫ ∫ ∞ −∞ f (τ ) f (t τ )dτ 2 0 = 1 − ∫ ∞ ①f2(t)为有始函数 f2 (t) = ( ) 0 0 0 2 ≥ < f t t t

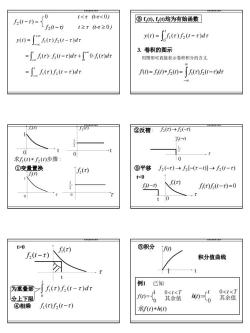
t0③积分f(t)fi(t)f(t-t)积分值曲线t例1已知为重叠部[ fi(t)fz(t-t)dt0<t<T0<1<TC1f(0)=0)=L0其余值分上下限其余值④相乘”fi(t)f,(t-t)求f(t)*h(t)

9 信号与系统电子课件 y (t) f (τ ) f (t τ )dτ = 1 2 − ∫ +∞ −∞ f τ f t τ dτ f τ dτ t t ( ) ( ) 0 ( ) ∫ 1 2 ∫ 1 +∞ −∞ = ⋅ − + ⋅ f τ f t τ dτ t ( ) ( ) = 1 2 − ∫−∞ f 2 (t −τ ) = 0 t 0 ( ) 1f τ τ t ( ) 2f t −τ ④相乘 ( ) ( ) 1 2 f τ f t −τ 为重叠部 分上下限 信号与系统电子课件 ⑤积分 f(t) t t : 积分值曲线 求f (t)∗h(t) h(t)= 0 t 0<t <T f (t) = 0 其余值 1 0<t <T 其余值 例1 已知

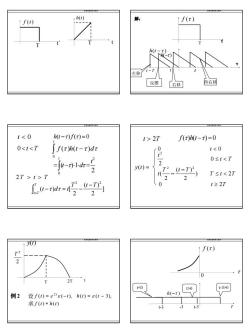
h(t)f(t)f(t)T左移再右移反挡右移t2T0t>21≥2T0T?_(-T)J(t-t)dt=122yt)t f(t)30K0t>0h(-t)例 2 设f(0)=e"e(-1), h(0)=e(t-3),求f(1) * h(0)+

10 信号与系统电子课件 t f (t) T t h(t) T 信号与系统电子课件 h(t − τ ) t − T t 左移 右移 t 再右移 τ f (τ ) T 解： τ 反摺 h(−τ ) 信号与系统电子课件 t t > T ] 2 ( ) 2 ( ) [ 2 2 T t T t d t T t T − − = − ∫ − τ τ 信号与系统电子课件 t > 2T f (τ)h(t −τ) =0 y(t) = 0 t 0 t-3>0