《机械测试技术基础》课程教学资源（作业习题）机械测试技术基础习题答案（第三版）

机械工程测试技术基础习题解答 教材：机械工程测试技术基础，熊诗波黄长艺主编，机械工业出版社，2006年9月第3版第二次印刷。 绪论 01叙述我国法定计量单位的基本内容。 解答：教材P45,二、法定计量单位。 0-2如何保证量值的准确和一致？ 解答：（参考教材P46,二、法定计量单位~五、量值的传递和计量器具检定》 1、对计量单位做出严格的定义： 2、有保存、复现和传递单位的一整套制度和设备： 3、必须保存有基准计量器具，包括国家基准、副基准、工作基准等。 3、必须按检定规程对计量器具实施检定或校准，将国家级准所复现的计量单位量值经过各级计算标 准传递到工作计量器具。 0-3何谓测量误差？通常测量误差是如何分类表示的？ 解答：（教材P810,八、测量误差 0-4请将下列诸测量结果中的绝对误差改写为相对误差。 ①1.0182544V47.8uV ②25.04894±0.00003)3 ③(5.48240.026)gcm 解答 ①±7.8×10/1.0182544≈±7.6601682/10 ②±0.00003/25.04894≈±1.197655/106 ③±0.026/5.482≈4.743% 0-5何谓测量不确定度？国际计量局于1980年提出的建议《实验不确定度的规定建议书 NC-1(1980)》的要点是什么？ 解答： ()测量不确定度是表征被测量值的真值在所处量值范围的一个估计，亦即由于测量误差的存在而对被 0-6为什么选用电表时，不但要考虑它的准确度，而且要考虑它的量程？为什么是用电表时应尽可能 地在电表量程上限的三分之二以上使用？用量程为150V的0.5级电压表和量程为30V的1.5级电压表分 别测量25V电压，请问哪一个测量准确度高？ 解答： ()因为多数的电工仪表、热工仪表和部分无线电测量仪器是按引用误差分级的（例如，精度等级为 0.2级的电表，其引用误差为0.2%)，而 引用误差=绝对误差/引用值 其中的引用值一般是仪表的满度值（或量程），所以用电表测量的结果的绝对误差大小与量程有关。量程越 大，引起的绝对误差越大，所以在洗用电表时，不但要考虑它的准确度，而且要考虑它的量程。 (2)从(1)中可知，电表测量所带来的绝对误差=精度等级×量程/100，即电表所带来的绝对误差是一定的 这样，当被测量值越大，测量结果的相对误差就越小，测量准确度就越高，所以用电表时应尽可能地在电 表量程上限的三分之二以上使用。 (3)150V的0.5级电压表所带来的绝对误差-0.5x150/100-0.75V:30V的1.5级电压表所带来的绝对误 差=1.5×30/100=0.45V。所以30V的1.5级电压表测量精度高

机械工程测试技术基础习题解答 教材：机械工程测试技术基础，熊诗波 黄长艺主编，机械工业出版社，2006 年 9 月第 3 版第二次印刷。 绪 论 0-1 叙述我国法定计量单位的基本内容。 解答：教材 P4~5，二、法定计量单位。 0-2 如何保证量值的准确和一致？ 解答：（参考教材 P4~6，二、法定计量单位~五、量值的传递和计量器具检定） 1、对计量单位做出严格的定义； 2、有保存、复现和传递单位的一整套制度和设备； 3、必须保存有基准计量器具，包括国家基准、副基准、工作基准等。 3、必须按检定规程对计量器具实施检定或校准，将国家级准所复现的计量单位量值经过各级计算标 准传递到工作计量器具。 0-3 何谓测量误差？通常测量误差是如何分类表示的？ 解答：（教材 P8~10，八、测量误差） 0-4 请将下列诸测量结果中的绝对误差改写为相对误差。 ①1.0182544V±7.8μV ②(25.04894±0.00003)g ③(5.482±0.026)g/cm2 解答： ① -6 6 ± ´ »± 7.8 10 /1.0182544 7.6601682/10 ② 6 ± »± 0.00003/25.04894 1.197655/10 ③ ± » 0.026/5.482 4.743Œ 0-5 何谓测量不确定度？国际计量局于 1980 年ᨀ出的建议《实验不确定度的规定建议书 INC-1(1980)》的要点是什么？ 解答： (1)测量不确定度是表征被测量值的真值在所处量值范围的一个估计，亦即由于测量误差的存在而对被 测量值不能肯定的程度。 (2)要点：见教材 P11。 0-6 为什么选用电表时，不但要考虑它的准确度，而且要考虑它的量程？为什么是用电表时应尽可能 地在电表量程上限的三分之二以上使用？用量程为 150V 的 0.5 级电压表和量程为 30V 的 1.5 级电压表分 别测量 25V 电压，请问哪一个测量准确度高？ 解答： (1)因为多数的电工仪表、热工仪表和部分无线电测量仪器是按引用误差分级的（例如，精度等级为 0.2 级的电表，其引用误差为 0.2%），而 引用误差=绝对误差/引用值 其中的引用值一般是仪表的满度值(或量程)，所以用电表测量的结果的绝对误差大小与量程有关。量程越 大，引起的绝对误差越大，所以在选用电表时，不但要考虑它的准确度，而且要考虑它的量程。 (2)从(1)中可知，电表测量所带来的绝对误差=精度等级×量程/100，即电表所带来的绝对误差是一定的， 这样，当被测量值越大，测量结果的相对误差就越小，测量准确度就越高，所以用电表时应尽可能地在电 表量程上限的三分之二以上使用。 (3)150V 的 0.5 级电压表所带来的绝对误差=0.5×150/100=0.75V；30V 的 1.5 级电压表所带来的绝对误 差=1.5×30/100=0.45V。所以 30V 的 1.5 级电压表测量精度高

0-7如何表达测量结果？对某量进行8次测量，测得值分别为：802.40,802.50,802.38,80248,802.42， 802.46,802.45,802.43。求其测量结果. 解答： ()测量结果=样本平均值土不确定度 或X=+=+方 (2)x= =802.44 8 x-对 5=8-1 =0.04035 d-店=014268 所以测量结果=-802.44+0.014268 0-8用米尺逐段丈量一段10m的距离，设丈量1m距离的标准差为0.2mm。如何表示此项间接测量的 函数式？求测此10m距离的标准差。 解答：山L=∑4 ea-成6m 09直圆柱体的直径及高的相对标淮差均为0.5%，求其体积的相对标准差为多少？ 解答：设直径的平均值为d,高的平均值为万，体积的平均值为下，则 p-d2% 4 4- =2a+ra 所号-4侣+[会-40s8w+05g=1%

0-7 如何表达测量结果？对某量进行 8 次测量，测得值分别为：802.40，802.50，802.38，802.48，802.42， 802.46，802.45，802.43。求其测量结果。 解答： (1)测量结果=样本平均值±不确定度 或 ˆ x s X x σ x n =+ =+ (2) 8 1 802.44 8 i i x x = = = å 8 2 1 ( ) 0.040356 8 1 i i x x s = - = = - å ˆ 0.014268 8 x s σ = = 所以 测量结果=802.44+0.014268 0-8 用米尺逐段丈量一段 10m 的距离，设丈量 1m 距离的标准差为 0.2mm。如何表示此项间接测量的 函数式？求测此 10m 距离的标准差。 解答：(1) 10 1 i i L L = = å (2) 2 10 2 1 0.6mm L Li i i L σ σ = L æ ö ¶ = = ç ÷ ¶è ø å 0-9 直圆柱体的直径及高的相对标准差均为 0.5%，求其体积的相对标准差为多少？ 解答：设直径的平均值为d ，高的平均值为h ，体积的平均值为V ，则 2 4 πd h V = ( ) ( ) 22 2 2 2 22 2 2 2 2 2 2 2 4 2 V dh d h d h V V πdh πd σ σ σ σ σ d h σ σ V V d h æö æö æ ö ¶ ¶ æ ö = += + ç÷ ç÷ ç ÷ ç ÷ èø èø è ø ¶ ¶ è ø æö æö = + ç÷ ç÷ èø èø 所以 2 2 2 2 V dh 4 4(0.5%) (0.5%) 1.1% σ σ σ V dh æöæö = += + = ç÷ç÷ èøèø

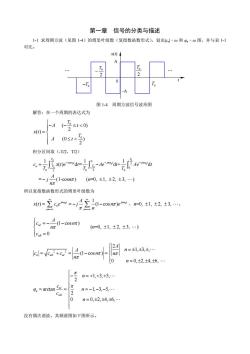
第一章信号的分类与描述 1求周期方波（见图1-4）的傅里叶级数（复指数函数形式），划出c-w和。-w图，并与表1日 对比 x(1) 图14周期方波信号波形图 解答：在一个周期的表达式为 A<0 x(t)= A0s1<2) 积分区间取(-T2,T2) 所以复指数函数形式的傅里叶级数为 0-立ce心=-20-wm,同23. n=0,±1，±2，±3，) c=0 24 n=1,3,土，. 0 n=0,2,4,6,. _元 n=+1,+3,+5,. 2 9=arctan CaL= n=-1,-3,-5,. C n=0,2,4,6, 没有偶次谐波。其频谱图如下图所示

第一章 信号的分类与描述 1-1 求周期方波（见图 1-4）的傅里叶级数（复指数函数形式），划出|cn|™ω 和 φn™ω 图，并与表 1-1 对比。 解答：在一个周期的表达式为 0 0 ( 0) 2 ( ) (0 ) 2 T A t x t T A t ì - - £< ïï = í ï £ < ïî 积分区间取（-T/2，T/2） 0 0 0 00 0 0 0 2 2 0 0 00 2 2 1 11 () d= d+ d = (1-cos ) ( =0, 1, 2, 3, ) T T jn t jn t jn t c x t e t Ae t Ae t n T T T TT A j nn n - - - - = - - ±±± ò òò L w ww p p 所以复指数函数形式的傅里叶级数为 0 0 1 ( ) (1 cos ) jn t jn t n n n A xt ce j n e n ¥ ¥ =-¥ =-¥ = =- - å å w w p p ， n=0, 1, 2, 3, ±±± L。 (1 cos ) ( =0, 1, 2, 3, ) 0 nI nR A c n n n c ì ï =- - í ±± ± ï = î L p p 2 2 2 1, 3, , (1 cos ) 0 0, 2, 4, 6, n nR nI A A n c c c n n n n ì ï =± ± ± = += - = í ï î = ±±± L L p p p 1, 3, 5, 2 arctan 1, 3, 5, 2 0 0, 2, 4, 6, nI n nR π n c π φ n c n ì - =+ + + ï ï ï = = =- - - í ï ï = ±±± ï î L L L 没有偶次谐波。其频谱图如下图所示。 图 1-4 周期方波信号波形图 0 t x(t) T0 2 - T0 2 -T0 ˆ ˆ A -A T0

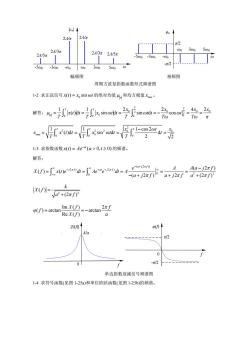
幅频图 相频图 周期方波复指数函数形式频谱图 1-2求正弦信号x)=xosin c1的绝对均值4和均方根值xm· 无-0-父面-停-g山-者 1-3求指数函数x()=Ae“(a>0,1≥0)的频谱。 解答： X(f)=["x(t)e-rr'di=[Ae-"eir'di=A- A xU-r+2an k o=arctan m(」 Rex(f =-arctan2f π/2 单边指数衰减信号频谱图 1-4求符号函数（见图1-25a)和单位阶跃函数（见图1-25b)的频谱

1-2 求正弦信号 0 xt x ( ) sin = ωt 的绝对均值 x μ 和均方根值 rms x 。 解答： 0 0 00 2 2 0 0 00 0 1 1 2 2 42 ( )d sin d sin d cos T T T T x x x xx μ xt t x ωt t ωt t ωt TT T Tω Tω π = = = =- = = òò ò 2 2 22 0 0 rms 0 00 0 1 1 1 cos 2 ( )d sin d d 2 2 TT T x x ωt x xt t x ωtt t TT T - == = = òò ò 1-3 求指数函数 ( ) ( 0, 0) at x t Ae a t - = >³ 的频谱。 解答： ( 2) 2 2 0 2 2 0 ( 2) ( ) () ( 2 ) 2 (2 ) a j ft j f t at j f t e A Aa j f X f x t e dt Ae e dt A aj f aj f a f - + ¥ ¥ - - ¥ -¥ - = = = == -+ + + ò ò p p p p p pp 2 2 ( ) (2 ) k X f a f p = + Im ( ) 2 ( ) arctan arctan Re ( ) Xf f f Xf a = =- p j 1-4 求符号函数(见图 1-25a)和单位阶跃函数(见图 1-25b)的频谱。 |cn| φn π/2 -π/2 ω ω ω0 ω0 3ω0 5ω0 3ω0 5ω0 2A/π 2A/3π 2A/5π 幅频图 相频图 周期方波复指数函数形式频谱图 2A/5π 2A/3π 2A/π -ω0 -5ω0 -3ω0 -5ω0 -3ω0 -ω0 单边指数衰减信号频谱图 f |X(f)| A/a 0 φ(f) 0 f π/2 -π/2

sgn(/) a)符号函数 b)阶跃函数 图1-25题14图 a)符号函数的频谱 0=o0-代8 处可不予定义，或规定sgO0 该信号不满足绝对可积条件，不能直接求解，但傅里叶变换存在， 可以借助于双边指数衰减信号与符号函数相乘，这样便满足傅里叶变换的条件。先求此乘积信号x) 的频谱，然后取极限得出符号函数x()的频谱。 x0=esg0=仁e0 「emt>0 x0=sgn)=lim￥() xU0=xoerah=-eeh+eeewh=-a+2T 4πf XUn-Fe0j小-吗Xn- w- 1 p(f)= f>0

a)符号函数的频谱 1 0 ( ) sgn( ) 1 0 t xt t t ì+ > = = í î- = = í î- ïî t sgn(t) 0 1 -1 t u(t) 0 1 图 1-25 题 1-4 图 a)符号函数 b)阶跃函数

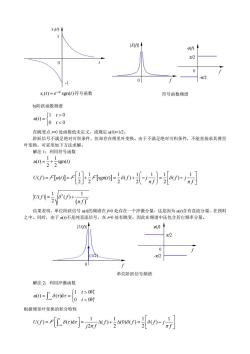
x() 0 2 0 /2 x()=esgn(t)符号函数 符号函数频谱 b)阶跃函数频谱 w0-6e8 在跳变点0处函数值未定义，或规定M0)F12。 阶跃信号不满足绝对可积条件，但却存在傅里叶变换。由于不满足绝对可积条件，不能直接求其傅里 叶变换，可采用如下方法求解。 解法1：利用符号函数 M0=+7gn0 u)-Ft-t- U1=550 1 (πf) 结果表明，单位阶跃信号)的频谱在0处存在一个冲激分量，这是因为认0含有直流分量，在预料 之中。同时，由于)不是纯直流信号，在0处有跳变，因此在频谱中还包含其它频率分量。 IUUM1 2 0 12 π/2 01 单位阶跃信号频谱 解法2：利用冲激函数 0-foar-6 根据傅里叶变换的积分特性 Un=f[arar]4nr4on-8n- 1

b)阶跃函数频谱 1 0 ( ) 0 0 t u t t ì > = í î = = í î < ò 时 时 根据傅里叶变换的积分特性 11 1 1 ( ) ( )d ( ) (0) ( ) ( ) 22 2 t Uf f f f j jf f dt t d d -¥ p p é ù é ù = = D +D = - ê ú ê ú ë û ë û ò F 单位阶跃信号频谱 f |U(f)| 0 (1/2) f φ(f) 0 π/2 -π/2 1 ( ) sgn( ) at xt e t - = 符号函数 t x1(t) 0 1 -1 符号函数频谱 f φ(f) 0 π/2 0 f |X(f)| -π/2

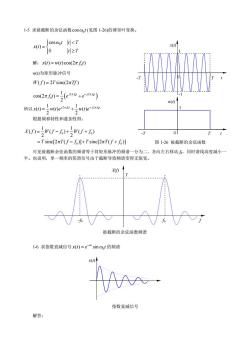
1-5求被战断的余弦函数c0s,1(见图1-26)的傅里叶变换。 m-6v457 解：x()=w()cos(2πf） w0)为矩形脉冲信号 W(f)=2 Tsinc((2πf） eos2r0=eaw+ee） 所以0=)n0e2s+与m0eW 根据频移特性和叠加性得： x=U-)+U+0 0 =Tsinc2πTf-f6月+Tsinc[2πTf+f6】 图1-26被截断的余弦函数 可见被截断余弦函数的频谱等于将矩形脉冲的频谱一分为二，各向左右移动6，同时谱线高度减小一 半。也说明，单一频率的简谐信号由于截断导致频谱变得无限宽。 XU) 6 被截断的余弦函数频谱 16求指数衰减信号x()=e“sino,1的频谐 x() A 指数衰减信号 解答

1-5 求被截断的余弦函数 0 cosω t (见图 1-26)的傅里叶变换。 0 cos ( ) 0 ω ttT x t t T ì < ï = í ï ³ î 解： 0 xt wt ft ( ) ( ) cos(2 ) = p w(t)为矩形脉冲信号 W f T Tf ( ) 2 sinc(2 ) = p ( ) 0 0 2 2 0 1 cos(2 ) 2 j ft j ft ft e e p p p - = + 所以 0 0 1 1 2 2 () () () 2 2 j ft j ft xt wte wte- = + p p 根据频移特性和叠加性得： 0 0 0 0 1 1 () ( ) ( ) 2 2 sinc[2 ( )] sinc[2 ( )] Xf Wf f Wf f T Tf f T Tf f = -+ + = -+ + p p 可见被截断余弦函数的频谱等于将矩形脉冲的频谱一分为二，各向左右移动 f0，同时谱线高度减小一 半。也说明，单一频率的简谐信号由于截断导致频谱变得无限宽。 1-6 求指数衰减信号 0 ( ) sin at xt e ω t - = 的频谱 解答： 指数衰减信号 x(t) f X(f) T -f0 f0 被截断的余弦函数频谱 图 1-26 被截断的余弦函数 t -T T t -T T x(t) w(t) 1 0 0 1 -1

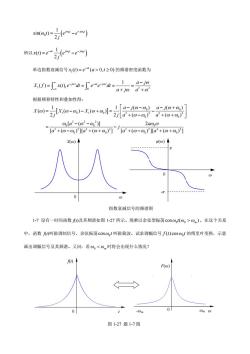
sin(o)) 所以0=eew-e） 单边指数衰减信号x)=e“(a>0,1≥0)的频谱密度函数为 小-mc-orea号 根据频移特性和叠加性得： oj-a-oi-xa+a二-二别】 aa2-(o2-21 +(o-,]++,J+o-1a+o+万 X(@) -t 指数衰减信号的频谱图 1-7设有一时间函数)及其频谱如图1-27所示。现乘以余弦型振荡c0s0,(,>0)。在这个关系 中，函数)叫做调制信号，余弦振荡cos,1叫做载波。试求调幅信号f)cosa的傅里叶变换，示意 画出调幅信号及其频谱。又问：若)，<0时将会出现什么情况？ 图1-27题1-7图

( ) 0 0 0 1 sin( ) 2 jt jt t ee j - = - w w w 所以 ( ) 0 0 1 ( ) 2 at jt jt xt e e e j - - = - w w 单边指数衰减信号 1 ( ) ( 0, 0) at xt e a t - = >³ 的频谱密度函数为 1 1 2 2 0 1 ( ) () j t at j t a j X f x t e dt e e dt aj a ¥ ¥ - - -¥ - = = == + + ò ò w w w w w 根据频移特性和叠加性得： [ ] 0 0 1 01 0 2 22 2 0 0 2 22 00 0 2 22 2 2 22 2 00 00 1 1 () () () ( ) ( ) 2 2 () () [ ( )] 2 [ ( ) ][ ( ) ] [ ( ) ][ ( ) ] aj aj XX X j ja a a a j aa aa é ù - -+ = - + = - ê ú ë û +- ++ - - = - +- ++ +- ++ ww ww w ww ww ww ww w w w ww ww ww ww ww 1-7 设有一时间函数 f(t)及其频谱如图 1-27 所示。现乘以余弦型振荡 0 0 cos ( ) ωt ω > ωm 。在这个关系 中，函数 f(t)叫做调制信号，余弦振荡 0 cosω t 叫做载波。试求调幅信号 0 f t( ) cosω t 的傅里叶变换，示意 画出调幅信号及其频谱。又问：若ω0 < ωm 时将会出现什么情况？ 图 1-27 题 1-7 图 ω F(ω) 0 f(t) 0 t -ωm ωm 0 0 X(ω) -π π φ(ω) ω ω 指数衰减信号的频谱图

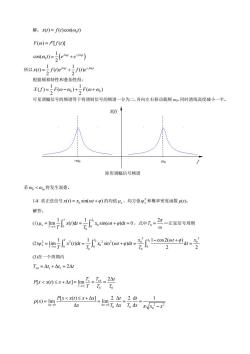
解：x0=f)cos(a,) F(@)=Af()] cosa,)=ew+em） 所以0=)j0e+f0em 根据频移特性和叠加性得： X(-F-)+F(@+0) 可见调幅信号的频谱等于将调制信号的频谱一分为二，各向左右移动载频，同时谱线高度减小一半。 矩形调幅信号频谱 若<0n将发生混叠。 1-8求正弦信号x()=xsi(a1+p)的均值4，、均方值和概率密度函数p). 解答： 0%=-0-片6ma侧+p=0,式中五-名-E装指苦 ew-er0地=2 xsr(ar+pw-l-2-号 2 (3)在一个周期内 T0=△1+△2=2A 作0a归导-号尝 To 网-马创只异总盖 △x

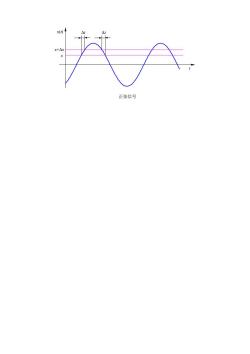
解： 0 xt f t t ( ) ( ) cos( ) = w F ft ( ) [ ( )] w = F ( ) 0 0 0 1 cos( ) 2 jt jt t ee- = + w w w 所以 0 0 1 1 () () () 2 2 jt jt xt f te f te- = + w w 根据频移特性和叠加性得： 0 0 1 1 () ( ) ( ) 2 2 Xf F F = -+ + ww ww 可见调幅信号的频谱等于将调制信号的频谱一分为二，各向左右移动载频 ω0，同时谱线高度减小一半。 若ω0 < ωm 将发生混叠。 1-8 求正弦信号 0 xt x ( ) sin( ) = + ωt φ 的均值 x μ 、均方值 2 ψx 和概率密度函数 p(x)。 解答： (1) 0 0 0 0 0 1 1 lim ( )d sin( )d 0 T T x T μ xt t x ωt φ t ®¥ T T = = += ò ò ，式中 0 2π T ω = —正弦信号周期 (2) 0 0 2 2 2 2 22 0 0 0 00 0 0 0 1 1 1 cos 2( ) lim ( )d sin ( )d d 2 2 TT T x T x x ωt φ ψ xt t x ωt φ t t ®¥ TT T - + = = += = òò ò (3)在一个周期内 T tt t x0 12 =+= Δ Δ 2Δ 0 0 0 2Δ [ () Δ ] lim x x T T T t Px xt x x ®¥ TT T < £+ = = = Δ 0 Δ 0 2 2 0 0 0 [ () Δ ] 2 Δ 2d 1 ( ) lim lim x x Δ Δ d Px xt x x t t p x x T xTx π x x ® ® < £+ = = == - f X(f) ω0 -ω0 矩形调幅信号频谱

正弦信号

x(t) 正弦信号 x x+Δx Δt Δt t