《信号与系统》课程教学资源（习题解答）第五章 拉普拉斯变换与系统分析

CIEE第五章拉普拉斯变换与系统分析本章重点（1）利用性质求双边拉氏变换及其收敛域（2）单边拉氏变换的时移、尺度变换、时域卷积、微分和积分性质的应用条件（3）接入周期信号的拉氏变换（4）求波形描述的信号的拉氏变换的几种方法（5）含指数函数或二阶共轭极点的拉氏变换求逆方法（6）初终值定理的应用条件及利用初值定理求零输入响应（7）微分方程表征的系统的s域分析例5.1求下列函数的双边拉氏变换及其收敛域(a) e"ce(0)+e*"*(-1)(b) te-l , a>0(c) e(at +b)(d) sin(ot +0)e()解(a）因为c.le"(0)l--_， Re[]>-as+a,[e-"e(-)]-_, Re[]b时e,[e"e()+es(-)]--$+a-s+b~-a<Re[]<-b(1)当α<b时，信号组合以后拉氏变换的收敛域为空集，故拉氏变换不存在。（2）当a=b时，相当于e-的拉氏变换，这是收敛域仍为空集，故其拉氏变换不存在。相应地sinot=-e-io）的拉氏变换也不存在，而sinots(）的拉氏变换为了，sinal-e(-）的拉氏变换为，但它们结合后的双边拉氏s2+0?变换的收敛域为空集，即变换不存在（注意，其频谱为两个冲激）,[e-e(0)]=te"()+te"e(-1)（b）

CIEE CAU 第五章 拉普拉斯变换与系统分析 本章重点 （1）利用性质求双边拉氏变换及其收敛域 （2）单边拉氏变换的时移、尺度变换、时域卷积、微分和积分性质的应用条件 （3）接入周期信号的拉氏变换 （4）求波形描述的信号的拉氏变换的几种方法 （5）含指数函数或二阶共轭极点的拉氏变换求逆方法 （6）初终值定理的应用条件及利用初值定理求零输入响应 （7）微分方程表征的系统的 s 域分析 例 5.1 求下列函数的双边拉氏变换及其收敛域 （a）e () ( ) t e t at bt + − − − ε ε （b） a t te − ，a > 0 （c）ε ( ) at + b （d）sin( ) ωt +θ ε (t) 解 （a） 因为 [ ] ( ) s a e t at b + = − 1 l ε ，Re[s] > −a [ ] ( ) s b e t bt b + − − = − 1 l ε ， Re[s] b 时 [ ] () ( ) s a s b e t e t at bt b + − + + − = − − 1 1 l ε ε ， − a < Re[s] < −b （1） 当 a < b 时 ，信号组合以后拉氏变换的收敛域为空集，故拉氏变换不存在。 （2） 当 a = b 时，相当于 at e− 的拉氏变换，这是收敛域仍为空集，故其拉氏变换 不存在。 相应地 ( ) j t j t e e j t ω ω ω − = − 2 1 sin 的拉氏变换也不存在，而sinωt ⋅ε ( )t 的拉氏变 换为 2 2 ω ω s + ，sinωt ⋅ε ( ) − t 的拉氏变换为 2 2 ω ω + − s ，但它们结合后的双边拉氏 变换的收敛域为空集，即变换不存在（注意，其频谱为两个冲激） （b） [te ( )t ] te (t) te ( t) a t at at b = + − − − − l ε ε ε

CAUCIEE其中e le"s(0]- +a]'，Re[]>-c e l- aka所以，-a0-Re[>0a,[(a+)-[(+)]o[1e,Re[]>0当a>0时福.e",Re[]>0当a0例5.2 求下列函数的单边拉氏变换(a) te(-)e(t-1)(b) te-(+)e(t+1)(c) 6(2t-1)

CIEE CAU 其中 [ ] ( ) ( )2 1 s a te t at b + = − l ε ， Re[s] > −a [ ] ( ) ( )2 1 s a te t at b + − l ε − = ， Re[s] 0 [ ] ( ) a s a a a s at b = ⋅ = 1 1 l ε ，Re > 0       a s [ ] ( ) [ ] [ ]        − ⋅ > > = = ⋅                     + = + 当 时 当 时 ,Re 0 0 1 ,Re 0 0 1 e s a s e s a s e a s a a b at b a t s a b s a b s a b b b l ε l ε 注意两点，（1）双边拉氏变换的尺度变换性质中 a 可 正可负，而单边拉氏变换要求 a 为正；（2）时移和尺度变换均是对自变量t 进行的，若认为ε (at + b) 是时移 b 则 会得到错误的结果。 （d） [ ] ( ) () [ ] ( ) ( ) [ ( ) ()] 2 2 cos sin sin sin sin cos cos sin ω ω θ θ ω θ ε ω θ ε ω θε ω θε + ⋅ + ⋅ = + = + = + s s t t t t t t t t b b l l l Re( )s > 0 例 5.2 求下列函数的单边拉氏变换 （a） ( ) ( ) 1 3 − − − te t t ε （b） ( ) ( ) 1 3 + − + te t t ε （c）δ ( ) 2t −1

CAUCIEE(d)ale'coste()解 (a) (le-(-)e(t-1)]l-(--1)e-(-),e -e(t-1)+e-(-).,e2 -e(t-1)因为4(e(0) -10-der-0l- -1-0-所以e2 . e-- _ (s+2)e2-sde-(-)e(t-1)]=e~.7(s+1)2$+1(s+1)(b) le-(+)(++1)]=te-(+);()=1-e-.ec()=7(s +1)注意，ε(+1）的拉氏变换与s(）的拉氏变换相同。类似地，当1>0时(5.2. 1)f(0)-e(t+to)= fo(0)-c(t+t0)-s(0)= fo(0)-c(0)单边拉氏变换的时移定理为r(t-t0),e(-10)]-F(s)e"应用时需要函数的个部分1均有相同的时移t。，且要求1o>0，若<0则按式（5.2.1)处理(c)(6(0)]=-1e[0(t -1)]= e~s(6(21-1)=-1e（d）求解该题要用到拉氏变换的微分性质，单边拉氏变换在分析具有初始条件的因果LTI

CIEE CAU （d） e t ( )t dt d t cos ε 2 2 − 解（a） ( ) [ ( )] ( ) ( ) ( ) ( ) 1 1 1 ( 1) 3 1 2 1 2 − = − ⋅ ⋅ − + ⋅ ⋅ − − − − − − − te t t e e t e e t t t t l ε ε ε 因为 [ ] ( ) s t 1 l ε = [ ( )] 1 1 + = − s e t t l ε [ ( )] ( )2 1 1 + = − s te t t l ε ( ) ( ) [ ] ( ) ( )2 1 1 1 1 + − − = − − − s e t e t s t l ε 所以 ( ) [ ] ( ) ( ) ( ) ( )2 2 2 2 3 2 1 2 1 1 1 + + = + + ⋅ + − = ⋅ − − − − − s s e s e e s e te t e s s s t l ε （b） ( ) [ ] ( ) ( ) () () ( )2 3 3 3 3 1 1 + + = = ⋅ ⋅ = − − + − + − − s e te t te t t e e t t t t l ε ε ε 注意，ε ( ) t +1 的拉氏变换与ε ( )t 的拉氏变换相同。类似地， 当 t0 > 0 时 [ ] f ( )t ⋅ε (t + t ) = f ( )t ⋅ε (t + t )⋅ε (t) = f (t)⋅ε (t) 0 0 0 0 0 l （5.2.1） 单边拉氏变换的时移定理为 [ ] ( ) ( ) ( ) 0 0 0 st f t t t t F s e− l − ⋅ε − = 应用时需要函数的个部分 t 均有相同的时移 0t ，且要求t0 > 0 ，若t0 < 0 则 按 式 （5.2.1） 处理 （c） l[ ] δ ( )t = 1 [ ] ( ) s t e− l δ −1 = [ ] ( ) 2 2 1 2 1 s t e − l δ − = （d）求解该题要用到拉氏变换的微分性质，单边拉氏变换在分析具有初始条件的因果 LTI

CIECAI系统中起着重要的作用，其基础正是时域微分性质。单边拉氏变换中的积分下限的取法有0㎡和0+两种，分别称为拉氏变换的0-和0+系统，在两种系统中时域微分性质有所不同，这里采用0"系统。采用0-系统可以避免0到0*的跳变问题，而将之包含在拉氏变换式中，因为doste(0l=亨ele- coste(0)]- (s+1)° +1所以"coste()s2(s+1)- sr(o-)- '(o-)(s +1)° +1又因信号是因果的，(o-)=(o-)=0所以[ d?e'coste(0)]= 5(s+1)(s+1)2 +1Ldt例5.3求图5.3.1所示各接入周期信号的拉氏变换+ f(0)+70（0)0+()2T(a)(6)图5.3.1解 （a）由题图5.3.1（a）可得F(0)= 8()+ 8(t-T)+ 8(t- 2T)+ 8(t-3T)+o(t-nT令第一周期内的信号以@）表示，则(0)=8()F()=1由图可知重复周期为T，于是

CIEE CAU 系统中起着重要的作用，其基础正是时域微分性质。单边拉氏变换中的积分下限的取法有 − 0 和 + 0 两种，分别称为拉氏变换的 − 0 和 + 0 系统，在两种系统中时域微分性质有所不 同，这里采用 − 0 系统 。采用 − 0 系统可以避免 − 0 到 + 0 的跳变问题，而将之包含在 拉氏变换式中，因为 [ ] ( ) 1 cos 2 + = s s l tε t [ ] ( ) ( ) 1 1 1 cos 2 + + + = − s s e t t t l ε 所以 ( ) ( ) ( ) () () − − − − − ′ + + + =       0 0 1 1 1 cos 2 2 2 2 sf f s s s e t t dt d t l ε 又因信号是因果的， ′(0 ) = (0 ) = 0 − − f f 所以 ( ) ( ) ( ) 1 1 1 cos 2 2 2 2 + + +  =      − s s s e t t dt d t l ε 例 5.3 求图 5.3.1 所示各接入周期信号的拉氏变换 图5.3.1 ( ) a (b) T 2 T 3 T 1 2 3 4 f (t) t L o o L ( ) 1 ( ) 1 ( ) 1 ( ) 1 t f ( )t 解 （a）由题图 5.3.1（a）可得 () () ( ) ( ) ( ) ( ) ∑ ∞ = = + − + − + − + = − 0 2 3 n f t δ t δ t T δ t T δ t T L δ t nT 令第一周期内的信号以 f ( )t 1 表示，则 f (t) = δ (t) 1 ( ) 1 F1 s = 由图可知重复周期为T ，于是

CAUCIEEF(s)= F,(s) 1-e"1-e-(b）由图5.3.1（b）可得(0)= (0)-c(-1)F()-1-"_ 1-eSsS重复周期T=3，于是1_1-e1-eF(s)= F(s) -1-e-sts'1-e-3s"s(1-e-3)设①为一有限持续周期信号，即有(0)= (0)[s(0)-c(t- T)]接入周期信号(）可表示为f()-(t-nT)其拉氏变换F(s）与第一周期信号（即f(））的拉氏变换F(s）的关系为F()= F() 1-e(5.3.1)例5.4求如图5.4.1所示各信号的拉氏变换f()+(0)6-1to+t(a)(b)图5.4.1解这是典型的用波形描述的信号的拉氏变换求解问题，利用性质我们可灵活的求解。（a）该例有多种解法，下面分别介绍【解法一]利用时域微分性质、积分性质d2将了()进行两次微分，得1()C）的波形图如图5.4.2所示

CIEE CAU () () sT sT e e F s F s − − − = − = ⋅ 1 1 1 1 1 （b） 由图 5.3.1（b）可得 ( ) ( ) ( 1) f1 t = ε t − ε t − ( ) s e s e s F s −s −s − = − = 1 1 1 重复周期 T = 3 ，于是 () () ( ) s s s s st s e e s e e e F s F s 1 3 3 1 1 1 1 1 1 1 − − − − − − − = − ⋅ − = − = ⋅ 设 f ( )t 1 为一有限持续周期信号，即有 f ( )t = f (t)[ε (t)− ε (t − T )] 1 1 接入周期信号 f ( )t 可表示为 f () ( ) t f t nT n = ∑ − ∞ =0 1 其拉氏变换 F( )s 与第一周期信号 （即 f (t) 1 ）的拉氏变换 F (s) 1 的关系为 () () st e F s F s − − = ⋅ 1 1 1 （5.3.1） 例 5.4 求如图 5.4.1 所示各信号的拉氏变换 a +τ 0t 0 t 1 f ( )t t o o t f (t) −τ 0t 1 2 3 4 ( ) a (b) 图 5 . 4 . 1 解 这是典型的用波形描述的信号的拉氏变换求解问题，利用性质我们可灵活的求解。 （a）该例有多种解法，下面分别介绍 [解法一]利用时域微分性质、积分性质 将 f ( )t 进行两次微分，得 f ( )t dt d 和 f ( )t dt d 2 2 的波形图如图 5.4.2 所示

CIECAU++驾1(9)(2)fo-tfo-tto+Te(a)(6)图5.4.20)=(-(0-)-8(-0)+8(-(6+)2e-(6-/_ 24e-0+=e利用时域微分性质s°F(s)-sr(o-)- (o-)由图可知(o-)=0(o-)=0于是sF(0)-r0)-e(-)一般地，设 d(6)=40，则有dt0(s) = sF(s)- T(0-)若已知d()及(o-）。可两边除以s得F()=10(s)+ 0)其中！可能引入S=0这一极点

CIEE CAU (b ) τ a +τ 0t 0 t ( ) dt df t o −τ 0t ( ) a 图 5 . 4 . 2 τ a − t t τ a − −τ 0 o t 0 t +τ 0t       τ a       τ a      − τ 2a ( ) 2 2 d dt f t ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 0 0 0 2 0 0 0 0 2 2         = − + = −        = − − − − + − +      − − − − − − − s s t s t s t s t s e e e a e a e a e a t t a t t a t t a f t dt d τ τ τ τ τ τ τ τ δ τ τ δ τ δ τ τ l l 利用时域微分性质 () ( ) () () − − = − − ′       0 0 2 2 f t s F s sf f dt d l 由图可知 (0 ) = 0 − f ′(0 ) = 0 − f 于是 ( ) ( ) 2 2 2 2 2 0         = = − − − s s t s e e e a f t dt d s F s τ τ τ 一般地 ，设 ( ) ( ) dt df t Φ s = ，则有 ( ) ( ) ( ) − Φ s = sF s − f 0 若已知 Φ( )s 及 ( ) − f 0 。可两边除以 s 得 ( ) ( ) ( ) s f s s F s − = Φ + 1 0 其中 s 1 可能 引入 s = 0 这一极点

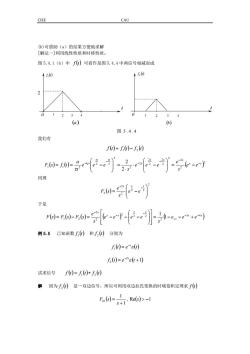
CIEECAU(b)可借助（a）的结果方便地求解【解法一]利用线性性质和时移性质图5.4.1（b）中）可看作是图5.4.4中两信号相减而成f(0)f0(a)(b)图5.4.4我们有(0)= f:(0)-f:()F(0)=J(0)=号e-0(-e号e2er-e(e-e)oe同理F:(s)--e于是F(s)= F(s)- F;(6)= (e-e-)-(es-e(i-e..-e-3s +e-+sS例5.5已知函数(）和(）分别为1(0)=e'c():(0)=e"e(t+1)试求信号10)=(0)*,0)解因为J(）是一双边信号，所以可利用双边拉氏变换的时域卷积定理求()F(0)= Re()>-1

CIEE CAU (b)可借助（a）的结果方便地求解 [解法一]利用线性性质和时移性质。 图 5.4.1（b）中 f (t) 可看作是图 5.4.4 中两信号相减而成 1 2 3 4 图 5 . 4 . 4 ( ) a (b) 1 2 3 4 f (t) 2 t o o t f ( )t 1 2 我们有 f (t) f (t) f (t) = 1 − 2 ( ) () ( )2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 2 2 2 0 s s s s s s s s t s e e s e e e e s e e e s a F s f t − − − − − − = −         ⋅ − ⋅ =         = = − τ τ τ 同理 ( ) 2 2 2 2 2 2         = − − − s s s e e s e F s 于是 () () () ( ) ( ) s s s s s s s s e e e s e e e e s e F s F s F s 3 4 2 2 2 2 2 2 1 2 1 1 − − − − − − = − − +                 = − = − − − 例 5.5 已知函数 f ( )t 1 和 f ( )t 2 分别为 f (t) e (t) t ε − 1 = ( ) ( 1) 2 2 = + − f t e t t ε 试求信号 f () () () t f t f t 1 2 = ∗ 解 因为 f ( )t 2 是一双边信号，所以可利用双边拉氏变换的时域卷积定理求 f ( )t ( ) 1 1 1 + = s F s b ,Re(s) > −1

CAUCIEFr2 (0)=1,[e-1e(t+1)]=l,[e-2().* (+1)]Re(s)>-225.102+5s+1利用时域卷积定理有F,()=l,[()*:(0)]= Fb1(s) Fr2(s)Re(s)>-1= e-2(+1). 2 .e(t+1)=e2+s(s +1)(s + 2)10)=1,e2(s +1)(s +2)2+5[]e-()s(t+1)-e-"s(t+1)直接进行时域卷积也能得到一致结果，但是若利用单边拉氏变换则会出现问题。计算如下：F,(0)--F,(s)=e*e(+1)=e-"s(0)"$+2于是F()-F(0)F:()=(+108+2)0-]-0问题在于单边拉氏变换的时域卷积定理要求两信号是因果的，本例f(）是一个非因果信号，e-"c(t+1)的拉氏变换与e-e()的拉氏变换一致，因而导致了错误的结果。例5.6求下列函数的拉氏反变换(a) F(6)=+I)

CIEE CAU ( ) [ ( )] ( ) [ ] ( ) 1 1 1 1 1 1 2 2 2 1 2 2 2 + = ⋅ + = ⋅ ⋅ = ⋅ ⋅ + = + + − + − s e s e e e e t F s e t s s t b t b b ε ε l l Re(s) > −2 利用时域卷积定理有 ( ) [ ( ) ( )] () () ( ) ( ) ( )( ) 1 2 1 1 2 2 1 2 1 2 1 2 + + = ⋅ = ⋅ ⋅ + = ⋅ = ∗ + − + s s e e e t F s F s F s f t f t s t b b b b ε l Re(s) > −1 ( ) ( )( ) ( ) ( ) ( ) () () 1 1 1 2 1 1 2 1 1 2 2 1 2 1 2 = + − +       + − + = ⋅       + + = ⋅ − − − + − + − + e t e t s e s e s s f t e t t s s b s b ε ε l l 直接进行时域卷积也能得到一致结果，但是若利用单边拉氏变换则会出现问题。计算如下： ( ) 1 1 1 + = s F s ( ) ( ) ( ) 2 1 1 2 2 2 + = = = + − − s e t F s e t t t ε ε 于是 () () () ( )( ) 1 2 1 1 2 + + = ⋅ = s s F s F s F s ( ) ( ) ( ) ( ) e e ( )t s s f t t t ε 2 2 1 1 1 − − = −       + ⋅ + = l 问题在于单边拉氏变换的时域卷积定理要求两信号是因果的，本例 f (t) 2 是一个非因果信 号， ( ) 1 2 + − e t t ε 的拉氏变换与e (t) t ε −2 的拉氏变换一致，因而 导致了错误的结果。 例 5.6 求下列函数的拉氏反变换 （a） ( ) ( )3 3 +1 = s s F s

CIEECAU3s +8_ (1-e)(b) F(s)=-+5s+6解（a）求拉氏反变换的常用方法是部分分式展开法和留数法，对于双边拉氏反变换还需考虑收敛域问题。【解法一】部分分式展开法只要函数T①)是指数信号的线性组合，其拉氏变换F(）就一定可以写成有理分式的A(s)形式:F(s)=。因而求反变换时可将其展开为部分分式的组合，各部分分式是常用BIs)信号的拉氏变换式，其反变换组合即是1C)本例F(s)是假分式，先画为真分式再展开F(0)-1-3+++1-1-5(0)-1-[Tkuk12ki3[+1*+1+(+](s + 1)3kt= F(s) (s+1)- =k2=-%F()(+)- =-3k-F(0)(+1)]-=-3于是F(s)=1-[+]r0)=6()-(Fre"--- - 31e"* + 3e(0)（b）在F(s)分式的分子中含有部分时，可以先将其分离出来，在求得其余部分的反变换后再利用时移性质求出F(s)的反变换。3s+8-(-e)= F(0)(1-e~)-[2-(i-e)F(6)=+2)5+3)$+2+$+3其中10=2e" ()+ e"-()所以

CIEE CAU （b） ( ) ( ) s e s s s F s − ⋅ − + + + = 1 5 6 3 8 2 解（a）求拉氏反变换的常用方法是部分分式展开法和留数法，对于双边拉氏反变换还需考 虑收敛域问题。 [解法一]部分分式展开法 只要函数 f ( )t 是指数信号的线性组合，其拉氏变换 F(s) 就一定可以写成有理分式的 形式： ( ) ( ) B( )s A s F s = 。因而求反变换时可将其展开为部分分式的组合，各部分分式是常用 信号的拉氏变换式，其反变换组合即是 f (t) 本例 F( )s 是假分式，先画为真分式再展开。 ( ) ( ) ( ) ( ) ( ) ( )      + + + + + = − = − + + + = − 1 1 1 1 1 1 3 3 1 1 13 2 12 3 11 3 1 2 s k s k s k F s s s s F s ( ) ( 1) 1 1 3 11 = 1 ⋅ + = s=− k F s s ()( ) 1 3 1 3 12 = 1 ⋅ + = − s=− F s s ds d k ()( ) 1 3 2 1 1 3 2 1 2 13 = ⋅ + = s=− F s s ds d k 于是 ( ) ( ) ( ) ( )      + + + − + + = − 1 3 1 3 1 1 1 3 2 s s s F s f () () t t t e te e ( )t t t t δ ε      = − − + − − − 3 3 2 1 2 （b）在 F( )s 分式的分子中含有 部分时，可以先将其分离出来，在求得其余部分的反变换 后再利用时移性质求出 F( )s 的反变换。 ( ) ( )( ) ( ) ( )( ) ( ) s s s e s s e F s e s s s F s − − − −       + + + ⋅ − = − = + + + = 1 3 1 2 2 1 1 2 3 3 8 1 其中 ( ) e () () t e t s s f t t t ε ε 2 3 1 2 3 1 2 2 − − = +       + + + = 所以

CAUCIE(0)=2e"-()+ "e(0)-[e-(-) +e-(-" (-1)例5.7求下列各函数的反变换的初值和终值(a) F(s)=$+1s-1() F()=)(c) F(a)=28t)s(s? +1)解(a）先将F(s)化为真分式F(s)=1+= 1+ F(s)于是f(o+)= J.(o+)= lim sF(s)= -2F(s）的极点S=-1在左半平面，故终值存在J(0) = lim sF(s)= 0(） 0)--1由于极点s=-1在左半平面，原点上的极点s=0为一阶，故终值存在，即(0)= lim sF(s)s-1= -1综合（a）和（b）求终值的结果可知，F(s)具有s=0这个一阶极点时终值不为零，否则终值为零。这是因为终值在对应两种情况1）极点在左半平面，相应的时域信号为衰减的，终值为零：2）一阶极点在原点，对应着阶跃信号，终值不为零。2s +1(）(0)-0因为F(s）在虚轴上有一对共轭极点s=，表明f()中含有正弦或余弦成分，故终值不存在，这可由其拉氏反变换验证

CIEE CAU ( ) () ( ) ( ) ( ) 2 [2 ] ( 1) 2 3 2 1 3 1 = + − + − − − − − − − f t e t e t e e t t t t t ε ε ε 例 5.7 求下列各函数的反变换的初值和终值 （a） ( ) 1 1 + − = s s F s （b） ( ) 2( ) 1 1 + − = s s F s （c） ( ) ( ) 1 2 1 2 + + = s s s F s 解 （a）先将 F( )s 化为真分式 ( ) F ( )s s F s 1 1 1 2 1 = + + − = + 于是 (0 ) (0 ) lim ( ) 2 = 1 = 1 = − →∞ + + f f sF s s F( )s 的极点 s = −1 在左半平面，故终值存在 ( ) lim ( ) 0 0 ∞ = = → f sF s s （b） ( ) ( ) 1 s s 1 s 1 0 lim = + − = ⋅ →∞ + f s s 由于极点s = −1在左半平面，原点上的极点s = 0 为一阶，故终值存在，即 ( ) ( ) ( ) 1 s s 1 s 1 lim lim 0 0 = − + − = ⋅ ∞ = → → s f sF s s s 综合 （a） 和（b） 求终值的结果可知， F(s)具有s = 0 这个一阶极点时终值不为零， 否则终值为零。这是因为终值在对应两种情况 1）极点在左半平面，相应的时域信号为衰减 的，终值为零；2）一阶极点在原点，对应着阶跃信号，终值不为零。 （c） ( ) ( ) 0 s s 1 2s 1 0 lim 2 = + + = ⋅ →∞ + f s s 因为 F( )s 在虚轴上有一对共轭极点 s = ±j ，表明 f (t)中含有正弦或余弦成分，故终 值不存在，这可由其拉氏反变换验证