《信号与系统》课程授课教案（课件讲稿）第6章 离散系统的Z域变换

可见，因果系列f(k)的单边Z变换和第六章离散系统的Z域变换双边Z变换相等8 6-1Z变换二.Z变换的收敛域一、定义1.定义- (0)++)+F(z) :ZF(K)z-单边Z 变换Zf(k)z -*F(z) =收敛域：当(n)为有界时，令上述F(z)- Z f(k)z -双边Z变换级数收敛的=的所有可取的值的集合称为收敛域F(2)-f)Z++ +(-IZ+(0)+JZ+ +f()典型序列的收敛域2①有限长序列[2/+8Z+0(k)= 「 (k)k,≤k≤k,收敛域：00k2kiib. k,>k ≥0收敛域：[z↓>0②右边序列（因果序列）收敛域：[2]> R,mc. k,<k,<0RE:f收敛半径m[]F(2)-2 f(k)z-kR2收敛域：Re[=][z<82626

1 k k F z f k Z − ∞ = = ∑0 单边 Z 变换 ( ) ( ) k k F z f k Z − ∞ = −∞ 双边 Z 变换 ( ) = ∑ ( ) §6-1 Z变换 第六章 离散系统的Z域变换 一、定义 可见，因果系列f(k)的单边Z变换和 双边Z变换相等 二. Z变换的收敛域 1. 定义 = ∑ = + + + " ∞ = −∞ − 2 (1) ( 2 ) ( ) ( ) ( 0 ) z f z f F z f k z f k k 收敛域：当 为有界时，令上述 级数收敛的 的所有可取的值的集 合称为收敛域. f (n) z ①有限长序列 a. k1 0 2. 典型序列的收敛域 f (k) = k为其它值 f k k k k 0 ( ) 1 ≤ ≤ 2 ∑= − = 2 1 ( ) ( ) k k k k F Z f k Z 1 k 2 k k f (k ) 1 2 ( ) ( ) ( 1) (0) (1) ( )2 1 1 k k F Z f k Z f Z f f Z f k Z − − − = +"+ − + + +"+ |Z|≠∞ Z≠0 收敛域 : 0 k1 ≥ 0 I m z R ze z =∞ f (k) 收敛域 : Z > 0 I m z R ze z =∞ 收敛域 : Z R R1 Re[z] j Im[z] 收敛半径 k k F z f k Z − ∞ = = ∑0 ( ) ( )

④双边序列③左边序列 (反因果序列)-2()2"F(z)=二(k)z-F(z) =-2 ()2*+2 (0)2-1m圆内为收敛域收敛域：[2R,jIm[3]收敛域：[zR,时有环行收敛域BelaRR,[0时上式收敛收敛域为整个平面Z+1.z-1ZIf(k)I=1.z +32 +2+2.z)F(2)=-z-a收敛域为：0lZ0并确定收敛域(b>a,b>0,a>0)b.双边Z变换k≥0解：这是一个双边序列/(k)={bkk≤-1Zf(k)z-k Za*u(k)-b*u(-k-1)z-kF(z)=a.求单边z变换F(2)-25(k)Z-*-2[a*u(k)+b*u(-k-1)Z-k2Zau(k)+ 2 (-b)z-

2 ③左边序列（反因果序列） 0 k 圆内为收敛域， R2 j Im[z] Re[z] 2 收敛域 : Z R 当R2 > R1时 有环行收敛域 R2 a 时上式收敛 z a z Fz − ( )= 并确定收敛域 例3. 求f (k) a u(k)- b u( k 1)的Z变换, k k = − − (b > a,b > 0,a > 0) 解：这是一个双边序列f (k ) = 1 0 − ≤ − ≥ b k a k k k a. 求单边Z变换 k k k k k k F z f k Z a u k b u k Z− ∞ = − ∞ = ( ) =∑ ( ) =∑[ ( ) + (− − 1)] 0 0 b. 双边Z变换 k k k k k k F z f k Z a u k b u k Z− ∞ =−∞ − ∞ =−∞ ( ) = ∑ ( ) = ∑[ ( ) − (− − 1)] k k k k k a u k b Z− − =−∞ ∞ = = ∑ ( ) + ∑ (− ) 1 0 z a z a z a Z k k k > − = = − ∞ = ∑ 0

三.常用系列的Z变换k=-nZa*z-k-1(-b")z"1.单位样值序列8(k)ZT[8(k)]=1a-+--a+2-b"a2. 单位阶跃序列 u(k)收敛域>06]1z-13 6-2Z变换的性质3. 指数序列f(k)=a*u(k)一、线性性质ZT[F(k)I-Za*z-k若 z(x(k)]=X(z)(Rl则 z[a(k)+by(k)l=aX(z)+bY(2) (R,某些线性组合中某些零点与极点相抵,J(k)=a'u(k-1)α则收敏域可能扩大。>0一x(k)-y(k)α()-Y(z)零极点相消，收敛域扩大为整个z平面

3 z b z z a z b z b z a z − + − = − − + − = 1 ⇓⇓ ⇓ 收敛域 z > a z − =∑ = ∞ = − z z z ZT u k Z k k 3. f (k) a u(k) k 指数序列 = ∑ ∞ = − = 0 [ ( )] k k k ZT f k a Z z a z a z > − = [ ] ( ) [ ] ( ) [ ] ( ) 1 2 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) Z ax k by k aX z bY z R z R Z y k Y z R z R Z x k X z R z R y y x x + = + a y(k) = ak u(k − 1) ↔ z > a x(k) − y(k) ↔ 零极点相消，收敛域扩大为整个z平面。 z a z X z − ( ) = z a a az az Y z a z k k k − = − = = − − − ∞ = ∑ 1 1 1 1 ( ) ( ) ( ) = 1 − − = − − − − == z a z a z a a z a z X z Y z

2.单边Z变换二、位移性若 x(k)谷X(z)1.双边Z变换且有整数m>0,Z[x(k)] = X(z)若x(k-1)αz-'X(z)+x(-1)Z[x(k -m)] = z-" X(z)X(k -2) z X(2)+ x(-2)+ X(-1)z-IZ[x(k+m)]= z"X(z)x(k-m)z"(z)+Ex(k-m)z-m为任意整数和x(k +1) 台zX(z)-x(0)z收效域：仅在z=0,z0处另加讨论其余同 X(z)x(k + 2) z'X(2) - x(0)z - x(1)zin(k+M)αz".311-M≤k≤Mz-1(k)f(k)= t)kM /tf(k)αz".二-z(m),2的双边Z变换z-1z-1解:F(k)=u(k+M)-μ|k-(M+1)z,22M+1-111(M)Aae三。Z域尺度变换特性四，时域卷积定理若ZT[x(k)]= X(2)Rxi<[2/<Rx2R<<Rm2若: ZT(k)I=X(z)则 ZTx(k)I=X()dR<<aRx2ZT[(k)I= H(z)Ru<1l<Rm2则x(k)*h(k)分X(2)H(2)Z()=例:收敛域max(Rs,Rm)<Z<min(Rz2,R2)Y.o则 ZT[enu(k)] =注：若收敛域边界上出现零极点相抵消.z-en7en. -1-则收敛域扩大

4 Z[ x(k m)] z X(z) −m − = Z[ x(k m)] z X (z) m + = 若 Z[ x(k )] = X (z) m为任意整数 ( ) : 0, , X z z z 其余同 收敛域 仅在 = = ∞处另加讨论 二. 位移性 1. 双边Z变换 2. 单边Z变换 若 x(k ) ↔ X (z) 且有整数m>0, ( 1) ( ) ( 1) 1 − ↔ + − − x k z X z x 2 1 ( 2) ( ) ( 2) ( 1) − − x k − ↔ z X z + x − + x − z k m k m x k m z X z x k m z − − = − ( − ) ↔ ( ) + ∑ ( − ) 1 0 x(k 2) z X (z) x(0)z x(1)z 2 2 + ↔ − − 和 x(k + 1) ↔ zX (z) − x(0)z # m k m k m x k m z X z x k z − = ( + ) ↔ ( ) − ∑ ( ) 0 解： f (k) = u(k + M ) − u[k − (M + 1)] 1 1 ( ) > − ↔ z z z ∵ u k 例2. 求图示长 度为2M+1的矩形序列 f (k ) = . . -M 0 M k k M k M M k M − ≤ ≤ 0 , 1 f (k) 的双边Z变换 − − + ↔ − + z z z u k M z M 1 - 1 ( ) ( 1) − ⋅ − ↔ ⋅ − + z z z z z f k z M M 1 1< z < ∞ 2 1 1 1 + + − ⋅ − = M M z z z z 三. Z域尺度变换特性 1 2 ZT[ ( )] ( ) X RX 若 x k = X z R < z < 1 2 ZT[ ( )] ( ) X X k aR z aR a z 则 a x k = X < < 例: 1 ZT[ ( )] − = z z u k 则 0 0 0 0 1 ZT[ ( )] Ω Ω Ω Ω − = − = j j j j k z e z e z e z e u k 则 x(k)∗h(k) ↔ X(z)H(z) 收敛域 max( , ) min( , ) Rx1 Rh1 < Z < Rx2 Rh2 注: 若收敛域边界上出现零极点相抵消. 则收敛域扩大. 1 2 ZT[ ( )] ( ) X RX 若: x k = X z R < z < 1 2 ZT[ ( )] ( ) h Rh h k = H z R < z < 四. 时域卷积定理

例题求下列两序列的卷积积分z-1= ZT-"[= ZT-1}=a'u(k)z-1z-ax(k)=u(k)h(k)=a'u(k)-a-u(k-1) [d1解收敛域[2>[alH(2)=ZTμu(k)-α-u(k-1)即收敛域比重叠部分大R()>a五．Z域微分特性z-a z-az-a若x(k)X(2)R14 -2- x(2)kx(k)-求ku(k)的z变换dzdz解：x(z)Kx(k)-l-zd-ZT[ku(k)]=---7(z-1)2dzz-1其中[-2元L=X(2))[1"(z-1)dzd2六 Z域积分特性七.K域反转特性若 x(k)X(2)R0. 则 X(ndn Ra aa"u(k)t-a设有整数m,且k+m>0,则求a-u(-k-1)的z变换。x(k) z"x(n)dn由x(-k) X(z"l)解k+ma-u(-k) --i-a1-azd

5 1 1 ZT[ ( )] > − = z z z 解∵: x k : 求下列两序列的卷积积分 ( ) ( ) ( ) ( ) ( 1) 1 1 = = − − − − = − − − = − 1 1 ( ) ( ) Z [X( ) ( )] 1 x k h k T z H z − ∴ ∗ = 收敛域 z > a 即收敛域比重叠部分大 五. Z域微分特性 jIm(z) R(z) e 0 a 1 1 2 ( ) ( ) x Rx 若 x k ↔ X z R − = z z z 1 1 6 : ZT[u ( )] > − = z z z 例 巳知 k 求ku(k)的z变换 六. Z域积分特性 1 2 ( ) ( ) x Rx 若 x k ↔ X z R ↔ 0, 则 η η η d X z k m x k z m m ∫ ∞ ↔ + + 1 ( ) ( ) 七. K域反转特性 1 2 ( ) ( ) x R x 若 x k ↔ X z R − ↔ z 例 8 : 巳知 ( )

九．初值定理用k+1代替k（左移1个单位）如果 k [al试利用Z变换的性质求下列的Z变换，并求：初始值了(0) 了(1), (2)注明收敛域。解：由初值定理(1) k(k -1)c(k - 1)f (0) -,4 2 -因为k6(k) (z-1)F()= lin2-a-2]=a所以 (k-1)e(k-1)z-)(z-1)2(z-1)21(2)-1417--azl-a

6 用k + 1代替k(左移1个单位 ) 1 1 1 ( 1) 1 a z z a az z a u k k − − = − − − − − ↔ 根据齐次性 , 两边均乘 a a z a z z a u k k 1 1 ( 1) − ( ) = 求 : 初始值 f ( 0 ), f (1 ), f ( 2 ) 解：由初值定理 ( 0 ) = 1 − = z a z f lin z → ∞ z a z a z f lin z − = − (1) = [ ⋅ ] z →∞ 2 2 2 ( 2 ) [ z az ] a z a z f lin z − − = − = ⋅ z →∞ （1）k(k −1)ε (k −1) 因为 2 ( 1 ) ( ) − ↔ z z k ε k 所以 2 2 1 ( 1) 1 ( 1) ( 1) ( 1) − = − − − ↔ ⋅ − z z z k ε k z 例: 已知 ( ) , z a z a k k − ε ↔ 2 ( 1) ( ) − ↔ z z kε k 试利用Z变换的性质求下列的Z变换，并 注明收敛域

k(k-1)8(k-1)-2是(2-))86.3逆2变换所以1.定义--2"-42*+32f(k)=ZT-"{F(z)](z -1)2.部分分式法[z/>1(2)(-1)* . ke(k)设F(z)为有理式，且只含一阶极点，解：(-1)*8(k)α 2+1通常先将F展开，再乘以2，即7#乙k.(-1) e(k) α-z>1F-2AF()-2 (z+1)2dz z+1②F(2)有共轭复数极点①F(2)具有单极点2z设z，z,为共轭复数，z3z,均为实数如收敛域为[> R，则r(k)为因果序列z2=c- jdz =c+ jdf(k)= Z A.(zm)"u(k)令α=+dβ=arctg若<Rz,则(k)为左边序列Cf(k)=-ZAm(zm)'u(-k-1)Z2 = ae-ip则 Z, =QejBF(2)F(2)有重极点++2A.z-z,1设 =zi处有重极点：A，A,为共轭复数令 A, = [Ale j0,A, - [4le-10F(z)+27:"e-y+@-++++[Alejoz -[Ale-jezA13+-A2-Fa(z) = -z-αe-ipz-22-epZ1- F.(2)+_4m因果序列：z-zmF.(k)=4lei(aei)*+4e-0(ae-i)*u(k)d i=11Au e-y.= 2|Aα* cos( βk + 0)u(k)Z

7 所以 4 3 2 2 ( 1) 4 3 ] ( 1) 1 ( 1) ( 1) [ − − + = − − − − ↔ − ⋅ z z z z dz z d k k ε k z （ z > 1 2）( 1) k (k) k − ⋅ ε 解： 1 ( 1 ) ( ) + − ↔ z z k k ε 2 ( 1) ) 1 ( 1) ( ) ( + = − + ⋅ − ↔ − z z z z dz d k k z k ε z > 1 §6.3 逆z变换 ( ) [ ( )] 1 f k ZT F z − 1. 定义 = 2. 部分分式法 通常先将 展 设 为有理式 且只含一阶极点 z F z F z ( ) ( ) , , 开, 再乘以 z, 即 ∑ − = m m m z z A z F (z) ∑ − = m m m z z zA F (z) n z z z z F z : , ," ( ) ① 具有单极点 1 2 如收敛域为 z > R1 , 则f (k)为因果序列 f ( k ) A (z ) u ( k ) m k = ∑ m m 若 z < R2 , 则f (k)为左边序列 f (k) = −∑ A (z ) u(−k − 1) m k m m z1 = c + jd z2 = c − jd ② 有共轭复数极点 z F (z) 设z1 , z2为共轭复数 , z3"zn均为实数 c d α = c +d β = arctg 2 2 令 则 1 2 β β α α j j z e z e − = = θ θ j j A A e A A A A e − = = 2 1 2 1 ∵ , 为共轭复数 , 令 , 2 2 1 1 ( ) z z A z z z A z F z a − + − = β θ β θ α α j j j j z e A e z z e A e z − − − + − = ∑= − + − + − = n m m m z z A z z A z z A z F z 2 3 2 1 1 ( ) 2 A cos( k )u ( k ) k = α β + θ f (k) [ Ae ( e ) Ae ( e ) ]u(k) j j k j j k a θ β θ β α α − − = + 因果序列： ③ 有重极点 z F ( z ) 设 z = z 1 处有 γ 重极点 ∑= − − + − + + − + − = n m m γ m γ γ z z A z z A (z z ) A (z z ) A z F z 1 2 1 1 1 12 1 11 ( ) " ∑ ∞ = − = + 2 ( ) m m a m z z A z F z 1 ] ( ) [( ) ( 1)! 1 1 1 1 1 . i z z i i z F z z z dz d i A − = − − − = γ

②2②=2,求道:变换4.--号4--2--解：极点：Z=z=±j2F@)-+ 4+ A.+1F(z) =z+1*z-ja*z+jd2-2+解之:4 -1.5 4 --1 4- A -与-16.42(2)* Ju(k)①>2(因果） (k)=[(-1)*,4z3+z3jd=αe学 -jd=αe α=2例3. F(z)=-，>1，求逆变换(2-1)(c-)F(z)AllA12-+A13Ja(k)= 1.58(k)-(-1)*u(k)解：(2-+7与(2) os(/ + 3.4 ) (k)A12 = 14 解之：Am=4fi(k) =F(k) = [4k (1)* + 14 (1)* + 3()* /u(k): (k)=1.58(k)-(-1)*u(k)+(2) cos(k+63.40)u(k)=[4k + 14 + 3() 1u(k)$ 6-4离散系统的z域分析例：已知离散系统的差分方程为一。 用2变换解差分方程y(k)-0.5y(k-1)= f(k)设n阶系统后向差分方程的一般形式其中f(k)=u(k), y(-1)=1, 求响应2.-3(k-1)-Zb-5(k- )解：两边取Z变换。根据单边Z变换的移=0时，了(k)接入：系统初始状态位特性，得为y(-1), (-2), y(-n)Y(2) - 0.5[Y(2)z- + y(-1)] = F(2)求解方法线性解方方程2变换 代数方程-待求量的Z变换Y(z)[1- 0.5z-j- 0.5 y(-1) = F(z)时域解【逆Z变换

8 ( 1 )( 2 ) 1 . ( ) 2 + − = z z z 例 F z ① z > 2 ② z 2(因果) ② z + + + = 解 : 极点 : z = − 1 z = ± j 2 z jd A z jd A z A z A z F z + + − + + = + 0 1 2 3 1 ( ) 解之: ° − ° = = − = = 63.4 3 63.4 0 1 2 4 5 4 5 1.5 1 j j A A A e A e 2 2 2 = − = = − α α α π π j j jd e jd e f (k ) 1.5 (k ) ( 1) u(k ) k a = δ − − 63.4 ) ( ) 2 (2) cos( 2 5 f (k ) k u k k b = + ° π 63.4 ) ( ) 2 (2) cos( 2 5 f (k) 1.5 (k) ( 1) u(k) k u k k k ∴ = − − + + ° π δ 例 求逆z变换 z z z z F z , z 1, ) 2 1 ( 1) ( 3. ( ) 2 3 2 > − − + = 2 ( 1 ) 1 1 ( ) 12 13 2 11 − + − + − = z A z A z A z F z 解： 4 14 3 解之： A11 = A12 = A13 = ) ] ( ) 2 1 f ( k ) [ 4 k (1 ) 14 (1 ) 3 ( u k k k k = + + ) ] ( ) 2 1 [ 4 k 14 3 ( u k k = + + §6-4 离散系统的z域分柝 一. 用z变换解差分方程 设n阶系统后向差分方程的一般形式 ( ) ( ) 0 0 a y k i b f k j m j m j n i ∑ k i − = ∑ − = − = − ( 1 ), ( 2 ), ( ). 0 , ( ) . y y y n k f k − − − = 为 " 时 接入 系统初始状态 求解方法 线性差分方程 代数方程 待求量的 Z变换 Z变换 时域解 逆Z变换 ( ) 0.5[ ( ) ( 1)] ( ) 1 Y z − Y z z + y − = F z − 解: 两边取Z变换. 根据单边Z变换的移 位特性, 得 其中f (k ) = u(k ), y(−1) = 1, 求响应 ( ) 0.5 ( 1) ( ) : y k − y k − = f k 例 巳知离散系统的差分方 程为 ( )[1 0.5 ] 0.5 ( 1) ( ) 1 Y z − z − y − = F z −

而零输入响应：0.5 y(-1)F(z)Y(z)=1-0.5z-Jr(k) = ZT -'[Y,(z)) = 0.5 .0.5*u(k)1-0.5z-1= (0.5)**+ (k)= Y (z)+ Y,(2)零状态响应：r(k)=ZT"[Y(z)]0.5 y(-1)0.5其中:Y(z)==1-0.52-而1-0.5z-1z2F(z)Y,(z)Y,(2)= 1- 0.52-TA.1 (z - 0.5)(z - 1)（z-0.5)(z-1)z - 0.5A, =2A, =-1A0.5z+(+)k20 =ai(k） （因果序列)则 Y,(z)= 2(--k<0k20-C=-α'u(-k-1)（反因果序列)Jf(k)=2[u(k)-(0.5)lu(k)=(2 -0.5*)u(k)全响应:y(k)=y,(k)+ (k)=(2-0.5*)u(k)+0.5*+* u(k)=(2-0.5*+l)u(k)例2.描述某LTI系统的差分方程为二．系统函数(传输函数)(k)-3(k-1)-25(k-2)= f(k)+2 (k-2)已知y(0)=2, 3(1)=7, 激励(k)=u(k), 求y(-1)和y(-2)y(k) = f(k)* h(k)(-1)。(-2)可由差分方程递推求得Z变换，则J(k-2)=(K)-(k-1)-(k)-2(k-2)Y(z)= F(z)H(z)f(t)y(t)(-1)=↓(()-(0)-{()-2(-I)令k=1h(k)离散系统的系统函数[721-0)=2H(2)-(2)零状态F(z)令k=(2(0)(022)2210若n阶LTI系统的后向差分方程为A26

9 1 1 1 0 .5 0 .5 1 0 .5 0 .5 ( 1 ) ( ) − − − = − − = z z y Y z 其中: x 1 0 .5 ( 0 .5 )( 1 ) ( ) ( ) 2 1 − − = − = − z z z z F z Y z f 1 1 1 0.5 ( ) 1 0.5 0.5 ( 1) ( ) − − − + − − = z F z z y Y z Y ( z ) Y ( z ) = x + f 而零输入响应: ( ) [ ( )] 0 .5 0 .5 ( ) 1 y k ZT Y z u k k x x = = ⋅ − ( 0 .5 ) ( ) 1 u k k + = 零状态响应: ( ) [ ( )] 1 y k ZT Y z f f − = 而 ( 0 .5 )( 1 ) 1 0 .5 ( ) 1 2 − + − = − − = z A z A z z z z Y z f A1 = 2 A2 = −1 ) 0.5 1 0.5 ( ) 2( − + − = − z z z z Y z 则 f ( ) 2[ ( ) (0.5) ( )] (2 0.5 ) ( ) 1 y k u k u k u k k k f = − = − + 全响应: y(k ) y (k ) y (k ) = f + x (2 0.5 ) ( ) 0.5 ( ) (2 0.5 ) ( ) 1 1 u k u k u k k k + k + = − + = − f 1(k) = 0 0 0 < ≥ k a k k 1. 引例： f2(k)= 0 0 0 < ≥ a k k k a u(k) (因果序列) k = = −a u(−k −1) (反因果序列) k 令k =1 例2. 描述某LTI系统的差分方程为 y(k ) − y(k − 1) − 2 y(k − 2) = f (k ) + 2 f (k − 2) 巳知 y(0) = 2, y(1) = 7, 激励 f (k ) = u(k ), 求y(−1)和y(−2). 解 : y(−1). y(−2)可由差分方程递推求得 [ ( ) ( 1) ( ) 2 ( 2)] 2 1 y(k − 2) = y k − y k − − f k − f k − [ (1) (0) (1) 2 ( 1)] 2 1 y(−1) = y − y − f − f − [7 2 1 0] 2 2 1 = − − − = 令k =0 2 1 [2 2 1 0] 2 1 [ (0) ( 1) (0) 2 ( 2)] 2 1 y(−2) = y − y − − f − f − = − − − = − 二．系统函数(传输函数) Z变换, 则 Y(z) = F(z)H(z) y(k) = f (k) ∗ h(k) ( ) ( ) ( ) F z Y z H z = 离散系统的系统函数 f (t) 零状态 y(t) h( k ) 若n阶LTI系统的后向差分方程为

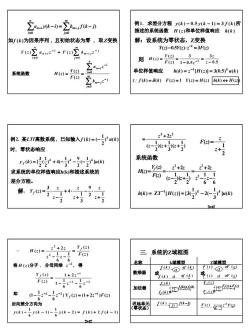
例1. 求差分方程 y(k)-0.5 y(k -1)=3 F(k)所f(k-j).V描述的系统函数H(z)和单位样值响应h(k)如(k)为因果序列，且初始状态为零，取z变换解：设系统为零状态，Z变换Y(2)-0.5Y(z)-Z- =3F()Y(z) an-i-1 - F(z)Zbm-jzY(z)37则 H(0)-1-0.5:-05Zani单位样值响应h(k)= z-[{H(2)]=3(0.5)*u(k)H(2)=Y() 系统函数F(z)E(f(k)=8(k) F(2)=1 Y(2)=H(2) (k)H(2)2 +222例2. 某LTI离散系统，已知输入F(k)=(-})*u(k)F(2)=-e-t+)时，零状态响应z+2系统函数()+(-()Y,(2) +2z2 +2zH(2)=求系统的单位样值响应h(k)和描述系统的差分方程。62-6解：Yy(2)=-+4.-h(k)= ZT-[(H(2)=[3()*-2(-→(k)22+2-z+3Y,(z)2°+2zH(z) = -三. 3系统的Z域框图F(z)2-1z-1名称k域模型乙域模型将H(2)分子。分母同乘 2-2,得FeO()[(k@()数乘器1+2z-1醇() a aF (s)Yy (z)或(k) a (5)FO-1-z(k)Etoiote(主(加法器即(1-I-↓)(2)-(+2-)F(c)联然秀后向差分方向为[(-)F()国F()(k)-g(k-1)-g(k-2)= F(k)+2f(k-1)

10 如f (k )为因果序列 , 且初始状态为零 , 取Z变换 ( ) ( ) 0 0 a y k i b f k j m j m j n i ∑ n i − =∑ − = − = − ∑ ∑ = − − = − − = = m j j m j n i i n i b z a z F z Y z H z 0 0 ( ) ( ) 系统函数 ( ) j m j m j i n i n i Y z a z F z b z − = − − = ∑ − = ∑ 0 0 ( ) ( ) ( ) ( ) 1. ( ) 0.5 ( 1) 3 ( ) H z h k y k y k f k 描述的系统函数 和单位样值响应 例 求差分方程 − − = 所 解：设系统为零状态，Z变换 ( ) 0.5 ( ) 3 ( ) 1 Y z − Y z ⋅z = F z − 0.5 3 1 0.5 3 ( ) ( ) ( ) 1 − = − = = − z z F z z Y z 则 H z ( ) [ ( )] 3(0.5) ( ) 1 h k z H z u k k = = 单位样值响应 − (∵ f (k) = δ (k) F(z) = 1 Y (z) = H(z) h(k) ↔ H(z)) ) ] ( ) 2 1 ( 2 9 ) 3 1 ) 4( 2 1 ( 2 3 y (k) [ u k k k k f = + − − − 时 零状态响应 例 某 离散系统 巳知输入 , ) ( ) 2 1 2. LTI , f (k) ( u k k = − 求系统的单位样值响应h(k)和描述系统的 差分方程。 解： 2 2 1 9 3 1 4 2 2 1 3 ( ) + − ⋅ + + ⋅ − = ⋅ z z z z z z Y z f ) 2 1 )( 3 1 )( 2 1 ( 2 3 2 − + + + = z z z z z 2 1 ( ) + = z z F z 系统函数 6 1 6 1 2 ) 2 1 )( 2 1 ( 2 ( ) ( ) ( ) 2 2 2 − − + = − + + = = z z z z z z z z F z Y z H z f ) ] ( ) 3 1 ) 2( 2 1 ( ) ZT [ ( )] [3( 1 h k H z u k k k = = − − − 将 H (z)分子 . 分母同乘 z −2 , 得 ( ) ( ) 6 1 6 1 2 ( ) 2 2 F z Y z z z z z H z f = − − + ∵ = 1 2 1 6 1 6 1 1 1 2 ( ) ( ) − − − − − + = z z z F z Y z f ) Y ( ) (1 2 ) ( ) 6 1 6 1 (1 1 2 1 z z z z F z f − − − 即 − − = + 后向差分方向为 ( 2 ) ( ) 2 ( 1 ) 6 1 ( 1 ) 6 1 y ( k ) − y k − − y k − = f k + f k − 名称 k域模型 Z域模型 f ( k ) a af ( k ) F ( z ) a aF ( z ) F ( z ) aF ( z ) a ( ) 1 f k ( ) 2 f k ( ) ( ) 1 2 f k + f k + ± ∑ ( ) 1 F z + ± ∑ ( ) 2 F z ( ) ( ) 1 2 F z +F z f ( k ) af ( k ) a f ( k ) f (k −1) D F (z) − 1 Z ( ) 1 z F z − 数乘器 或 或 加法器 迟延单元 （零状态） - - 三. 系统的Z域框图