《信号与系统》课程教学课件（讲义）信号与系统实验指导书（共八个实验）

信号与系统实验指导书精品课程建设课题组中国农业大学电子信息系2009.12

信号与系统实验指导书 精品课程建设课题组 中国农业大学电子信息系 2009．12

实验内容目录实验一典型电信号的观察与测量实验二零输入、零状态及完全响应实验三信号的采样与恢复实验四信号的（无失真）传输实验五非正弦周期信号的分解与合成实验六低通、高通、带通、带阻滤波器间的变换实验七付里叶变换、拉普拉斯变换、Z变换应用实验八系统的频域响应

实验内容目录 实验一 典型电信号的观察与测量 实验二 零输入、零状态及完全响应 实验三 信号的采样与恢复 实验四 信号的（无失真）传输 实验五 非正弦周期信号的分解与合成 实验六 低通、高通、带通、带阻滤波器间的变换 实验七 付里叶变换、拉普拉斯变换、Z 变换应用 实验八 系统的频域响应

实验一典型电信号的观察与测量一、实验目的1.学习TH-SG01P型功率函数信号发生器（本部分所指信号发生器均为此功率函数信号发生器）各旋钮、开关的作用及其使用方法。2．学习虚拟示波器（本部分所用示波器均为此虚拟示波器）的使用方法。二、实验设备1.信号与系统实验（一）挂件。2.TH-SGO1P型功率函数信号发生器。3.虚拟示波器。三、实验原理描述信号的方法有多种，可以是数学表达式（时间的函数），也可以是函数图形（即为信号的波形)。本实验主要是用电脑显示屏(即虚拟示波器)观测周期函数信号，如正弦波、方波、三角波、脉冲序列以及各种非正弦周期函数波形，每个波形都有它的波形参数，正弦波有其三要素即最大值、周期和初相，脉冲波有幅值、周期与脉宽占空比等参数，四、实验内容1.观察常用的信号，如正弦波、方波、三角波以及不同占空比的序列脉冲。2．用示波器测量信号，读取信号的各种参数，并记录波形。五、实验步骤1.连接虚拟示波器的并口通讯线，打开实验台上信号发生器的电源2．将信号发生器的输出端接到虚拟示波器的输入通道CH1或者CH2上，打开虚拟示波器窗口，观察不同函数波形，并测定它们的波形参数。六、实验报告1．根据实验测得的数据，绘制各个信号的波形图，并写出相应的数学函数表达式。实验二零输入、零状态及完全响应一、实验目的1．通过实验，进一步了解系统的零输入响应、零状态响应和完全响应的原理。2．掌握用简单的R-C电路观测零输入响应、零状态响应和完全响应的实验方法。二、实验设备1.信号与系统实验（一）2.虚拟示波器三、实验内容1．连接一个能观测零输入响应、零状态响应和完全响应的电路图（参考图2-1)

实验一 典型电信号的观察与测量 一、实验目的 1．学习 TH-SG01P 型功率函数信号发生器（本部分所指信号发生器均为此功率函数信 号发生器）各旋钮、开关的作用及其使用方法。 2．学习虚拟示波器（本部分所用示波器均为此虚拟示波器）的使用方法。 二、实验设备 1．信号与系统实验（一）挂件。 2．TH-SG01P 型功率函数信号发生器。 3．虚拟示波器。 三、实验原理 描述信号的方法有多种，可以是数学表达式（时间的函数），也可以是函数图形（即为 信号的波形）。 本实验主要是用电脑显示屏(即虚拟示波器)观测周期函数信号，如正弦波、方波、三角 波、脉冲序列以及各种非正弦周期函数波形，每个波形都有它的波形参数，正弦波有其三要 素即最大值、周期和初相，脉冲波有幅值、周期与脉宽占空比等参数。 四、实验内容 1．观察常用的信号，如正弦波、方波、三角波以及不同占空比的序列脉冲。 2．用示波器测量信号，读取信号的各种参数，并记录波形。 五、实验步骤 1．连接虚拟示波器的并口通讯线，打开实验台上信号发生器的电源。 2．将信号发生器的输出端接到虚拟示波器的输入通道 CH1 或者 CH2 上，打开虚拟示 波器窗口，观察不同函数波形，并测定它们的波形参数。 六、实验报告 1．根据实验测得的数据，绘制各个信号的波形图，并写出相应的数学函数表达式。 实验二 零输入、零状态及完全响应 一、实验目的 1．通过实验，进一步了解系统的零输入响应、零状态响应和完全响应的原理。 2．掌握用简单的 R-C 电路观测零输入响应、零状态响应和完全响应的实验方法。 二、实验设备 1．信号与系统实验（一） 2．虚拟示波器 三、实验内容 1．连接一个能观测零输入响应、零状态响应和完全响应的电路图（参考图 2-1）

2．分别观测该电路的零输入响应、零状态响应和完全响应的动态曲线。四、实验原理1．零输入响应、零状态响应和完全响应的模拟电路如图2-1所示。R0Io u(E=15VL图2-1零输入响应、零状态响应和完全响应的电路图2.图2-1中的开关K2拨到1处，则由回路可得iR+Uc=E(1)：i=c业。，则上式改为Rcle +U,=E(2)RCUe (S) -RCUe (0) +Ue (S) =对上式取拉式变换得：RCU(0）15其中U。(0)=5V.U (S)=S(RCS+1)RCS+1$+品s++5eRC(3)J(t)1-6ue(t)15F?10f/(1)图2-2零输入响应、零状态响应和完全响应曲线其中：①零输入响应②--零状态响应③-完全响应式(3)等号右方的第二项为零输入响应，即由初始条件激励下的输出响应；第一项为零状态响应，它描述了初始条件为零（Uc（0）=0）时，电路在输入E=15V作用下的输出响应，显然它们之和为电路的完全响应，图2-2所示的曲线表示这三种的响应过程五、实验步骤1.零输入响应将K；拨到2、K2拨到1，使+5V直流电源对电容C充电，待充电完毕后，将K2拨到2，用示波器观测Uc（t）的变化。2．零状态响应先将Kz拨到2，使电容两端的电压放电完毕，将Ki拨到1、Kz拨到1，用示波器观测15V直流电压向电容C的充电过程

2．分别观测该电路的零输入响应、零状态响应和完全响应的动态曲线。 四、实验原理 1．零输入响应、零状态响应和完全响应的模拟电路如图 2-1 所示。 图 2-1 零输入响应、零状态响应和完全响应的电路图 2．图 2-1 中的开关 K2 拨到 1 处，则由回路可得 iR+Uc＝E (1) ∵ i＝C dt dUc ，则上式改为 ＝E c U dt c dU RC + (2) 对上式取拉式变换得： RCUC（S）-RCUC（0）+UC（S）＝ S 15 ∴ RC 1 S 5 RC 1 S 15 S 15 ＝ RCS 1 RCU（0） S（RCS 1） 15 （S）＝ c U c + + + − + + +             ，其中 Uc(0)= 5V t RC 1 - 5e t RC 1 - （t）＝15 1 e c U +           − (3) 图 2-2 零输入响应、零状态响应和完全响应曲线 其中：①-零输入响应 ②-零状态响应 ③-完全响应 式(3)等号右方的第二项为零输入响应，即由初始条件激励下的输出响应；第一项为零 状态响应，它描述了初始条件为零（Uc（0）=0）时，电路在输入 E=15V 作用下的输出响 应，显然它们之和为电路的完全响应，图 2-2 所示的曲线表示这三种的响应过程。 五、实验步骤 1．零输入响应 将 K1 拨到 2、K2 拨到 1，使+5V 直流电源对电容 C 充电，待充电完毕后，将 K2 拨到 2， 用示波器观测 Uc（t）的变化。 2．零状态响应 先将 K2 拨到 2，使电容两端的电压放电完毕，将 K1 拨到 1、K2 拨到 1，用示波器观测 15V 直流电压向电容 C 的充电过程

3.完全响应先将K2拨到2，使电容两端电压通过R-C回路放电，一直到零为止。然后将Ki拨到2、K2拨到1，使5V电源向电容充电，待充电完毕后，再将Ki拨到1，使15V电源向电容充电，用示波器观测Uc（t）的完全响应。六、实验报告1.推导图2-1所示R-C电路在下列两种情况的电容两端电压Uc（t）的表达式。1)Uc(0)=0，输入U;=15V。2)Uc (0) =5V, 输入 U;=15V。2．根据实验，分别画出该电路的零输入响应、零状态响应和完全响应的曲线。七、实验思考题1.系统零输入响应的稳定性与零状态响应的稳定性是不是相同？2.若在RC串联电路的输入端施加一脉冲序列或方波激励信号，问Uc的响应线如何？实验三信号的采样与恢复一、实验目的1．了解电信号的采样方法与过程及信号的恢复。2.验证采样定理。二、实验设备1.信号与系统实验（一)。2.虚拟示波器。三、实验内容1．研究正弦信号被采样的过程以及采样后的离散化信号恢复为连续信号的波形。2.用采样定理分析实验结果。四、实验原理，离散时间信号可以从离散信号源获得，也可以由连续时间信号经采样而获得。采样信号fs（t）可以看成连续信号f（t）和一组开关函数S（t）的乘积。S（t）是一组周期性窄脉冲。由对采样信号进行傅立叶级数分析可知，采样信号的频谱包括了原连续信号以及无限多个经过平移的原信号频谱。平移的频率等于采样频率fs及其谐波频率2fs、3fs当平样后的信号是周期性窄脉冲时，平移后信号频率的幅度按（Sinx）/x规律衰减。采样信号的频谱是原信号频谱的周期性延拓，它占有的频带要比原信号频谱宽得多。2．采样信号在一定条件下可以恢复原来的信号，只要用一截止频率等于原信号频谱中最高频率n的低通滤波器，滤去信号中所有的高频分量，就得到只包含原信号频谱的全部内容，即低通滤波器的输出为恢复后的原信号。3.原信号得以恢复的条件是fs≥2B，其中fs为采样频率，B为原信号占有的频带宽度。Fmin=2B为最低采样频率。当fs2B三种采样频率对连续信号进行采样，以验证采样定理

3．完全响应 先将 K2拨到 2，使电容两端电压通过 R-C 回路放电，一直到零为止。然后将 K1拨到 2、 K2 拨到 1，使 5V 电源向电容充电，待充电完毕后，再将 K1 拨到 1，使 15V 电源向电容充 电，用示波器观测 Uc（t）的完全响应。 六、实验报告 1．推导图 2-1 所示 R-C 电路在下列两种情况的电容两端电压 Uc（t）的表达式。 1) Uc（0）=0，输入 Ui＝15V。 2) Uc（0）=5V，输入 Ui＝15V。 2．根据实验，分别画出该电路的零输入响应、零状态响应和完全响应的曲线。 七、实验思考题 1．系统零输入响应的稳定性与零状态响应的稳定性是不是相同？ 2．若在 RC 串联电路的输入端施加一脉冲序列或方波激励信号，问 Uc 的响应线如何？ 实验三 信号的采样与恢复 一、实验目的 1．了解电信号的采样方法与过程及信号的恢复。 2．验证采样定理。 二、实验设备 1．信号与系统实验（一）。 2．虚拟示波器。 三、实验内容 1．研究正弦信号被采样的过程以及采样后的离散化信号恢复为连续信号的波形。 2．用采样定理分析实验结果。 四、实验原理 1．离散时间信号可以从离散信号源获得，也可以由连续时间信号经采样而获得。采样 信号 fs（t）可以看成连续信号 f（t）和一组开关函数 S（t）的乘积。S（t）是一组周期性窄 脉冲。由对采样信号进行傅立叶级数分析可知，采样信号的频谱包括了原连续信号以及无限 多个经过平移的原信号频谱。平移的频率等于采样频率 fs 及其谐波频率 2fs、3fs· · ·。当采 样后的信号是周期性窄脉冲时，平移后信号频率的幅度按（Sinx）/x 规律衰减。采样信号的 频谱是原信号频谱的周期性延拓，它占有的频带要比原信号频谱宽得多。 2．采样信号在一定条件下可以恢复原来的信号，只要用一截止频率等于原信号频谱中 最高频率 fn 的低通滤波器，滤去信号中所有的高频分量，就得到只包含原信号频谱的全部 内容，即低通滤波器的输出为恢复后的原信号。 3．原信号得以恢复的条件是 fs≥2B，其中 fs 为采样频率，B 为原信号占有的频带宽度。 Fmin=2B 为最低采样频率。当 fs2B 三种采样频率对连续信号进行采样，以验证采样定理

要是信号采样后能不失真的还原，采样频率fs必须远大于信号频率中最高频率的两倍。2．下面的框图表示了对连续信号的采样和采样器低通滤波信号输入对采样信号的恢复过程。实验时，除选用足够高的采样频率外，还常采用前置低通滤波器来防止采样脉冲图3-1信号的采样与恢复原理框图信号频谱的过宽而造成采样后信号频谱的混选。五、实验步骤1．连接一采样信号（方波）发生器、采样器、低通滤波器组成的采样与恢复电路（可参考本实验台的“信号的采样与恢复”实验单元）2.在信号采样与恢复实验单元的输入端输入一频率为100Hz左右的正弦信号，然后调节方波发生器的输出频率在800Hz左右，观察采样输出信号以及通过低通滤波器后的恢复信号3．改变输入信号的频率，再观察采样输出信号以及通过低通滤波器后的恢复信号六、实验报告1．绘制原始的连续信号、采样后离散化信号以及采样信号恢复为原始信号的波形2．分析实验结果，并作出评述。实验四信号的（无失真）传输一、实验目的1．了解信号的无失真传输的基本原理。2．熟悉信号无失真传输系统的结构与特性。二、实验设备1.信号与系统实验台2.虚拟示波器三、实验内容1.设计一个无源（或有源）的无失真传输系统2．令幅值固定、频率可变化的正弦信号作为系统的输入信号，测量系统输出信号的幅值和相位（用李沙育图形法）。四、实验原理1．信号的无失真传输是指通过系统后输出信号的波形与输入信号的波形完全相同，只允许有幅值上的差异和产生定的延迟时间，具有这种特性的系统称为无失真传输系统。令输入信号为X（t)，则系统的输出为：Y(t)=KX(t-to)式中k、to为常量，对上式取付氏变换，则有Y(j) =kx (jo) e-j(io)2=ke oto=Hle-j0（a)H(jO)=X()H=k,k为常数，()=-to,to>0

要是信号采样后能不失真的还原，采样频率 fs 必须远大于信号频率中最高频率的两倍。 2． 下面的框图表示了对连续信号的采样和 对采样信号的恢复过程。实验时，除选用足够高 的采样频率外，还常采用前置低通滤波器来防止 信号频谱的过宽而造成采样后信号频谱的混迭。 图 3-1 信号的采样与恢复原理框图 五、实验步骤 1．连接一采样信号（方波）发生器、采样器、低通滤波器组成的采样与恢复电路（可 参考本实验台的“信号的采样与恢复”实验单元）。 2．在信号采样与恢复实验单元的输入端输入一频率为 100Hz 左右的正弦信号，然后调 节方波发生器的输出频率在 800Hz 左右，观察采样输出信号以及通过低通滤波器后的恢复 信号。 3．改变输入信号的频率，再观察采样输出信号以及通过低通滤波器后的恢复信号。 六、实验报告 1．绘制原始的连续信号、采样后离散化信号以及采样信号恢复为原始信号的波形。 2．分析实验结果，并作出评述。 实验四 信号的（无失真）传输 一、实验目的 1．了解信号的无失真传输的基本原理。 2．熟悉信号无失真传输系统的结构与特性。 二、实验设备 1．信号与系统实验台 2．虚拟示波器 三、实验内容 1．设计一个无源（或有源）的无失真传输系统。 2．令幅值固定、频率可变化的正弦信号作为系统的输入信号，测量系统输出信号的幅 值和相位（用李沙育图形法）。 四、实验原理 1．信号的无失真传输是指通过系统后输出信号的波形与输入信号的波形完全相同，只 允许有幅值上的差异和产生一定的延迟时间，具有这种特性的系统称为无失真传输系统。令 输入信号为 X（t），则系统的输出为： Y(t)=KX(t-t0) 式中 k、t0为常量，对上式取付氏变换，则有 ω） -jω0 Y（jω）＝kx（j e -jωt -j （ω） ＝ke ＝|H|e X（jω） Y（jω） H（jω）＝ 0 ϕ |H|＝k，k 为常数，φ(ω)= -t0ω，t0>0

2.实验电路系统图4-1无失真传输的电路图其中 R;=R-=20k Q, C=C2=1uF它的频率特性为：RU.(jw)1+jR,oH(jw)U,(jo)R.R, +R,I+jORC,*I+joR,c,五、实验步骤1.分析信号无失真传输系统的模拟电路，如图4-1所示。2．在模拟电路的输入端输入一个正弦信号，并改变其频率，用示波器观察输出信号的幅值和相位。六、实验报告1.画出信号无失真传输系统的模拟电路。2.分析无失真传输系统的结构特点，如果R;R2、C,+C，则系统的H（j)和p(o)会产生什么变化？七、实验思考题1．为什么输出信号波形与输入信号波形相同？2．信号的无失真传输系统与全通滤波器有何不同？实验五非正弦周期信号的分解与合成一、实验目的1：用同时分析法观测50Hz非正弦周期信号的频谱，并与其傅里叶级数各项的频率与系数作比较。2．观测基波和其谐波的合成。二、实验设备1.信号与系统实验（一）2.虚拟示波器三、实验原理1．任何电信号都是由各种不同频率、幅值和初相的正弦波选加而成的。对于周期信号由它的傅里叶级数展开式可知，各次谐波的频率为基波频率的整数倍。非正弦周期信号包含

2．实验电路系统 图 4-1 无失真传输的电路图 其中 R1=R2=20kΩ，C1=C2=1µF 它的频率特性为： ＝K R R R ＝ 1 jωR C R 1 jωR C R 1 jωR C R ＝ U（jω） U（jω） H（jω）＝ 2 1 2 2 2 2 1 1 1 2 2 2 i o + + + + + 五、实验步骤 1．分析信号无失真传输系统的模拟电路，如图 4-1 所示。 2．在模拟电路的输入端输入一个正弦信号，并改变其频率，用示波器观察输出信号的 幅值和相位。 六、实验报告 1．画出信号无失真传输系统的模拟电路。 2．分析无失真传输系统的结构特点，如果 R1≠R2、C1≠C2，则系统的 会产生什么变化？ 七、实验思考题 1．为什么输出信号波形与输入信号波形相同？ 2．信号的无失真传输系统与全通滤波器有何不同？ 实验五 非正弦周期信号的分解与合成 一、实验目的 1．用同时分析法观测 50Hz 非正弦周期信号的频谱，并与其傅里叶级数各项的频率与 系数作比较。 2．观测基波和其谐波的合成。 二、实验设备 1．信号与系统实验（一） 2．虚拟示波器 三、实验原理 1．任何电信号都是由各种不同频率、幅值和初相的正弦波迭加而成的。对于周期信号 由它的傅里叶级数展开式可知，各次谐波的频率为基波频率的整数倍。非正弦周期信号包含 H（jω）和ϕ(ω )

了从零到无穷大的所有频率成份，每一频率成份的幅值相对大小是不同的。将被测方波信号加到分别调谐于其基波和各奇次谐波频率的电路上。从每一带通滤波器的输出端可以用示波器观察到相应频率的正弦波。本实验的结构图如图5-1所示，其中所用的被测信号是50Hz的方波。2．实验装置的结构图LPFBPF1BPF2接示波器BPF3发生器交流毫伏表BPF4BPF5BPF6图5-1实验结构图图5-1中LPF为低通滤波器，可分解出非正弦周期信号的直流分量。BPF,~BPF。为调谐在基波和各次谐波上的带通滤波器，加法器用于信号的合成。3.各种不同的波形及其傅氏级数表达式方波(t)(sinat+sinat+sint+snot+T三角波u (t)=8(sinot-gsin3ot-sin5ot-)半波()=(+sinot-cosot-1Ccos4ot)全波u (t) = 4Um(1(cos2ot-Cos4ot-Ccos6ot矩形波2(sincosot+sin2cos20t+sincos3t+)u(t) =-T四、实验内容及步骤1.调节“功率函数信号发生器”，使其输出50Hz、幅度最大的方波信号，并将其接至信号分解实验模块的输入端，再细调函数信号发生器的输出频率，使该模块的基波50Hz成分BPF1的输出幅度为最大。2．将BPF1~-BPF6的输出分别接至虚拟示波器，观测各次谐波的幅值，并列表记录之。3.将方波分解所得的基波、三次谐波分别接至加法器的相应输入端，观测加法器的输

了从零到无穷大的所有频率成份，每一频率成份的幅值相对大小是不同的。将被测方波信号 加到分别调谐于其基波和各奇次谐波频率的电路上。从每一带通滤波器的输出端可以用示波 器观察到相应频率的正弦波。本实验的结构图如图 5-1 所示，其中所用的被测信号是 50Hz 的方波。 2．实验装置的结构图 图 5-1 实验结构图 图 5-1 中 LPF 为低通滤波器，可分解出非正弦周期信号的直流分量。BPF1～BPF6为调 谐在基波和各次谐波上的带通滤波器，加法器用于信号的合成。 3．各种不同的波形及其傅氏级数表达式 方波       + + + Sin7ωt +" 7 1 Sin5ωt 5 1 Sin3ωt 3 1 Sinωt π 4Um u（t）＝ 三角波       − − Sin5ωt −" 25 1 Sin3ωt 9 1 Sinωt π 8Um u（t）＝ 2 半波       + − − Cos4ωt +" 15 1 Cosωt 3 1 Sinωt 4 π 2 1 π 2Um u（t）＝ 全波       − − − Cos6ωt" 35 1 Cos4ωt 15 1 Cos2ωt 3 1 2 1 π 4Um u（t）＝ 矩形波       + + + Cos3ωt +" T 3τπ Sin 3 1 Cos2ωt T 2τπ Sin 2 1 Cosωt T τπ Sin π 2Um T τUm u（t）＝ 四、实验内容及步骤 1．调节“功率函数信号发生器”，使其输出 50Hz、幅度最大的方波信号，并将其接至 信号分解实验模块的输入端，再细调函数信号发生器的输出频率，使该模块的基波 50Hz 成 分 BPF1 的输出幅度为最大。 2．将 BPF1~BPF6 的输出分别接至虚拟示波器，观测各次谐波的幅值，并列表记录之。 3．将方波分解所得的基波、三次谐波分别接至加法器的相应输入端，观测加法器的输

出波形，并记录之。4．在步骤3的基础上，再将五次谐波分量加到加法器的输入端，观测相加后的合成波形，并记录之。5.分别将50Hz正弦半波、全波、矩形波和三角波的输出信号接至50Hz电信号分解与合成模块的输入端，观测其基波及各次谐波的频率和幅度，并记录之。6.将50Hz单相正弦半波、全波、矩形波和三角波的基波和谐波分量接至加法器相应的输入端，观测加法器的输出波形，并记录之。五、实验报告1．根据实验测量所得的数据，在同一坐标纸上绘制方波及其分解后所得的基波和各次谐波的波形，并画出其频谱图。2．将所得的基波和三次谐波及其合成后的波形一同绘制在同一坐标纸上。3．将所得的基波、三次谐波、五次谐波及三者合成的波形一同绘制在同一坐标纸上，并把实验步骤3所观测到的合成波形也绘制在同一坐标纸上，进行比较。六、实验思考题1．什么样的周期性函数没有直流分量和余弦项。2．分析理论合成的波形与实验观测到的合成波形之间误差产生的原因。实验六低通、高通、带通、带阻滤波器间的变换一、实验目的1.通过本实验进一步理解低通、高通和带通等不同类型滤波器间的转换关系。2．熟悉低通、高通、带通和带阻滤波器的模拟电路。二、实验设备1.信号与系统实验台2.虚拟示波器三、实验内容1：由低通滤波器变换为高通滤波器2.由高通滤波器变换为低通滤波器。3.在一定条件下，由低通和高通滤波器构成带通滤波器，4.在一定条件下，由低通和高通滤波器构成带阻滤波器。四、实验原理1.由于高通滤波器与低通滤波器间有着下列的关系：H(jo)=1-H(j0)(1)式中Ha(jα）为高通滤波器的幅频特性，H(jo）为低通滤波器的幅频特性。如果已知H(jo)，就可由式(1)求得对应的H(ja)；反之亦然。(2) 现令(Gj0)=1+RCjo

出波形，并记录之。 4．在步骤 3 的基础上，再将五次谐波分量加到加法器的输入端，观测相加后的合成波 形，并记录之。 5．分别将 50Hz 正弦半波、全波、矩形波和三角波的输出信号接至 50Hz 电信号分解与 合成模块的输入端，观测其基波及各次谐波的频率和幅度，并记录之。 6．将 50Hz 单相正弦半波、全波、矩形波和三角波的基波和谐波分量接至加法器相应 的输入端，观测加法器的输出波形，并记录之。 五、实验报告 1．根据实验测量所得的数据，在同一坐标纸上绘制方波及其分解后所得的基波和各次 谐波的波形，并画出其频谱图。 2．将所得的基波和三次谐波及其合成后的波形一同绘制在同一坐标纸上。 3．将所得的基波、三次谐波、五次谐波及三者合成的波形一同绘制在同一坐标纸上， 并把实验步骤 3 所观测到的合成波形也绘制在同一坐标纸上，进行比较。 六、实验思考题 1．什么样的周期性函数没有直流分量和余弦项。 2．分析理论合成的波形与实验观测到的合成波形之间误差产生的原因。 实验六 低通、高通、带通、带阻滤波器间的变换 一、实验目的 1．通过本实验进一步理解低通、高通和带通等不同类型滤波器间的转换关系。 2．熟悉低通、高通、带通和带阻滤波器的模拟电路。 二、实验设备 1．信号与系统实验台 2．虚拟示波器 三、实验内容 1．由低通滤波器变换为高通滤波器。 2．由高通滤波器变换为低通滤波器。 3．在一定条件下，由低通和高通滤波器构成带通滤波器。 4．在一定条件下，由低通和高通滤波器构成带阻滤波器。 四、实验原理 1．由于高通滤波器与低通滤波器间有着下列的关系： HH(jω）=1− HL(jω） (1) 式中 HH(jω）为高通滤波器的幅频特性， HL(jω）为低通滤波器的幅频特性。如果已知 HL(jω），就可由式(1)求得对应的 HH(jω）；反之亦然。 现令 1 RCjω 1 HL(jω） + = (2)

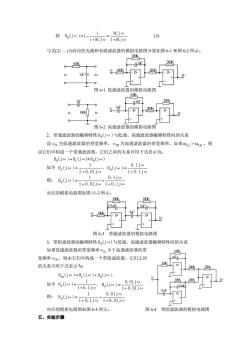
RCjw则 Ha(j)=1-1(3)1+RCjo 1+RCja与式(2）、(3)对应的无源和有源滤波器的模拟电路图分别如图6-1和图6-2所示。_100K江EL20kL膜KluF卡uoui图6-1低通滤波器的模拟电路图HluF10 u+图6-2高通滤波器的模拟电路图2．带通滤波器的幅频特性Hg(jα）与低通、高通滤波器幅频特性间的关系设Qα为低通滤波器的带宽频率，n为高通滤波器的带宽频率，如果のcL>cH，则由它们可构成一个带通滤波器，它们之间的关系可用下式表示为：Hg(jo)=H(j0)*H(j0)0.1ja如令 H(j)=,Hg(jo)=1+0.01ja1+0.1j00. 1ja则：H(j)=1+0.01j*1+0.1jo对应的模拟电路图如图 11-3所示10OKanilEt+I图6-3带通滤波器的模拟电路图3．带阻滤波器的幅频特性Hgjo）与低通、高通滤波器幅频特性间的关系如果低通滤波器的带宽频率α小于高通滤波器的带0k宽频率@cH，则由它们可构成一个带阻滤波器，它们之间的关系可用下式表示为：AANHs(jo)=H,(Gjo)+H(j0)200KJH(Go)-0.01ja如令H(jα)=o1+0.1j01+0.01j@L0.01jw则：H(jo)=10.1ja+1+0.01jc对应的模拟电路图如图6-4所示。图6-4带阻滤波器的模拟电路图五、实验步骤

则 1 RCjω RCjω 1 RCjω 1 H (jω） 1 H + = + = − (3) 与式(2) 、(3)对应的无源和有源滤波器的模拟电路图分别如图 6-1 和图 6-2 所示。 图 6-1 低通滤波器的模拟电路图 图 6-2 高通滤波器的模拟电路图 2．带通滤波器的幅频特性 HB(jω）与低通、高通滤波器幅频特性间的关系 设ω 为低通滤波器的带宽频率， CL ω 为高通滤波器的带宽频率，如果 CH ωCL > ωCH ，则 由它们可构成一个带通滤波器，它们之间的关系可用下式表示为： H (jω） H (jω)* H (jω) B = L H 如令 1 0.01jω 1 HL(jω） + = ， 1 0.1jω 0.1jω HH(jω） + = 则： 1 0.1jω 0.1jω 1 0.01jω 1 HB(jω） + × + = 对应的模拟电路图如图 11-3 所示。 图 6-3 带通滤波器的模拟电路图 3．带阻滤波器的幅频特性H (jω) B 与低通、高通滤波器幅频特性间的关系 如果低通滤波器的带宽频率ω 小于高通滤波器的带 CL 宽频率ω ，则由它们可构成一个带阻滤波器，它们之间 CH 的关系可用下式表示为： HBS (jω）= HL(jω）+ HH(jω） 如令 1 0.1jω 1 HL(jω） + = ， 1 0.01jω 0.01jω HH(jω） + = 则： 1 0.01jω 0.01jω 1 0.1jω 1 HB(jω） + + + = 对应的模拟电路图如图 6-4 所示。 图 6-4 带阻滤波器的模拟电路图 五、实验步骤