《电路》课程教学资源（PPT课件）第7章 二阶电路

第7章 二阶电路 重点掌握 二阶电路的零输入响应，零状态响应和全响应 学习方法 1.通过例子，掌握求解二阶电路的方法、步骤。 2.通过例子得出二阶电路的一般规律。 *本节讨论的具体结果只适用于本例，不能套用到 其它电路。但得出的规律具有一般性

1. 通过例子，掌握求解二阶电路的方法、步骤。 2. 通过例子得出二阶电路的一般规律。 * 本节讨论的具体结果只适用于本例，不能套用到 其它电路。但得出的规律具有一般性。 第7章 二阶电路 二阶电路的零输入响应，零状态响应和全响应 重点掌握 学习方法

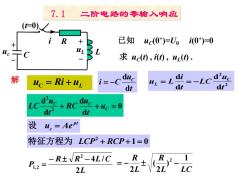
7.1二阶电路的零输入响应 (t-0) 已知uc(0)=U i(0)=0 L 求u(),(),uz(④. 解 uc Ri+u i=-Cduc dt u=L di =-LCduc dt dt2 +=0 dr2 dt 设W.=Ae 特征方程为LCP2+RCP+1=0 A.-C-±经 2L

7.1 二阶电路的零输入响应 uC = Ri + uL 0 d d d d 2 2 + + C = C C u t u RC t u LC pt 设 uc = Ae 1 0 2 特征方程为 LCP + RCP + = L R R L C P 2 4 / 2 1,2 −  − = L LC R L R 1 ) 2 ( 2 2 = −  − uC(0+ )=U0 i(0+ 已知 )=0 求 uC (t) , i(t) , uL (t) . t u i C C d d = − R L C + - i uc uL + - (t=0) 解 2 C 2 d d d d t u LC t i uL = L = −

根的性质不同，响应的变化规律也不同 R> L-C 二个不等负实根 uc =A ep+A,en R=2 二个相等负实根 uc =(A1+A,t)er R<2 二个共轭复根lc=Ked'sin(ot+B

根的性质不同，响应的变化规律也不同 2 二个不等负实根 C L R  2 二个相等负实根 C L R = 2 二个共轭复根 C L R  L LC R L R p 1 ) 2 ( 2 2 1,2 = −  − p t p t C u e e 1 2 = A1 + A2 pt C u (A A t)e = 1 + 2 sin(  )  = + − u Ke t t C

R>2,A,不等的负实根 (=0 uc Ajep+Azem:! 4c(0)=U→A,+A2=Uo 0)=-i0)=0→PA,+BA,=0 dt .U。 A=P.-P -U。 A:=P-P n(P,e-Pe) uc=P:-P

一. 2 p 1 , p 2 不等的负实根 CL R  p t p t C u e e 1 2 = A 1 + A 2 0 A 1 A 2 0 u C ( 0 ) = U → + = U + 0 A A 0 (0 ) (0 ) dd = → 1 1 + 2 2 = − = + + P P Ci tuC 0 2 1 1 0 2 2 1 2 A1 A U P PP U P P P −− = − = ( ) 1 2 2 1 2 1 0 p t p t C P e P e P P U u − − = R L C +- i u c u L+- ( t=0)

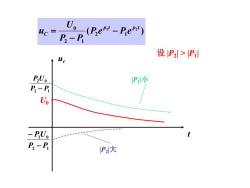
P-P (Be-pe) 设P2l>P1l Hc PUo P小 P2- U -PUo P2- P2大

( ) 1 2 2 1 2 1 0 p t p t C P e P e P P U u − − = U0 t uc 设 |P2 | > |P1 | 2 1 2 0 P P P U − |P1 |小 2 1 1 0 P P PU − − |P2 |大

U U uc=P.-P (Pev-Pe:) =0+=0, 行0=0 t>0 >0 2im t=tn时i最大 LCP2 RCP+1=0 4z(0)=U0 duc.-CUpe) i=-C dt 00 -U0 (:) t>im L(P:-P) i减小，u虹2tmuu衰减加快

( ) ( ) ( ) ( ) 1 2 1 2 2 1 0 1 2 1 2 2 10 p t p t C p t p t e e L P P U p p e p p e P P CU dt du i C − − − = − − − = − = t=0+ i=0 , t=  i=0 t = tm 时i 最大 00 t > tm i 减小, u L 2 tm u L 衰减加快 1 0 2 LCP + RCP + = t> 0 i>0 t U0 u c ( ) 1 2 2 1 2 1 0 p t p t C P e P e P P U u − − =

uc di U uL=L -U(Ben-P.e:) dt (P,-P) 由u=0可计算tm prepu-pzea=0 = =e(pz-p m P2 P2 tm= P2-P1 由duu/dt可确定w,为极小值的时间t piepu-pieps= ()=e In( =e(p2-p)t f= p2一=2tm P2 P2-P1

由 uL= 0 可计算 tm 0 1 2 1 − 2 = p t p t p e p e p p t p t p t e e e p p 2 ( ) 2 1 2 1 1 2 ( ) − = = 2 1 2 1 ln p p p p t m − = 由 duL / dt 可确定uL为极小值的时间t 0 1 2 2 2 2 1 − = p t p t p e p e p p t p t p t e e e p p ( ) 2 1 2 1 1 2 − = = m t p p p p t 2 ln( ) 2 1 2 2 1 = − = 2tm uL tm i t U0 uc ( ) ( ) 1 2 1 2 2 1 0 p t p t L P e P e P P U dt di u L − − − = =

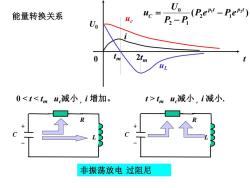
能量转换关系 ,(Pem-Pe:) Uo uc=P.-P 2im 0tmu减小，i减小. 非振荡放电过阻尼

能量转换关系 0 tm uc减小， i 减小. R L C + - R L C + - t U0 uc tm i 0 非振荡放电 过阻尼 ( ) 1 2 2 1 2 1 0 p t p t C P e P e P P U u − − = 2tm uL

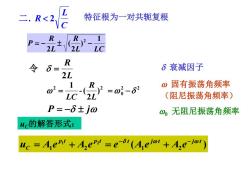
R 特征根为一对共轭复根 R 2LV 2L' 令 R 6衰减因子 21 02 1 R =06-62 ω固有振荡角频率 (阻尼振荡角频率) P=-6±jω ①，无阻尼振荡角频率 uc的解答形式： uc Aen+Aer:=e(A ejoi+Ae-io)

. 2 C L 二 R  特征根为一对共轭复根 L LC R L R P 1 ) 2 ( 2 2 = −  − P = −  j 2L R 令  = uC的解答形式： ( ) 1 2 1 2 1 2 p t p t t j t j t C u A e A e e A e A e −  −  = + = + 2 2 0 2 2 ) 2 -( 1  = = − L R LC  衰减因子  固有振荡角频率 （阻尼振荡角频率） 0 无阻尼振荡角频率

uc =A ep+Azeps =e-(A eiot+A,e-io) 式中A=D,-B ejot=cos@t+jsin@t P-P e-iot =cos@t-jsin@t P1,P2共轭A1,A2也共轭 uc =e(Ajeio+Aze-i) =e'[(A+A2)cos@t+j(A1-A2)sin@t] 实数 虚数 =e[Acos@t+Bsin@t] Ke-5'sin(at+B)

实数 虚数 e t j t e t j t j t j t       cos sin cos sin = − = + − [(A A )cos (A A )sin ] 1 2 1 2 e t j t t    = + + − − p1 ，p2 共轭 A1 ，A2 也共轭 A A (A A ) 1 2 1 2 1 2 p t p t t j t j t C u e e e e e −  −  = + = + sin(  )  = + − Ke t t (A A ) 1 2 t j t j t C u e e e −  −  = + e [Acos t Bsin t] t    = + − 0 2 1 2 A1 U P P P − = 0 2 1 1 A2 U P P P − − 式中 =