《信号与系统》课程授课教案（课件讲稿）第7章 系统函数

例：已知H(9)的零、极点分布图如示，并且h(0.)-2。求第七章系统函数H(S)的表达式。解：由分布图可得出87.1系统函数与系统特性HOG--7一、 系统函数的零、极点分布图根据初值定理，有LTI系统的系统函数是1O-%+)=lmsH(0)=m+25+50+复变量s或z的有理分式，即H0-742-A()=0的根p1’ P2..P,称为系统函数H()的极点B()-0的根，.，称为系统函数H(）的零点二、 系统函数H()与时域响应h()(b)若有一对共轭复极点pi2-α ±jB， 则A(s)中有因子[($+a)+B-eaicos(Bt+e)e(t)冲激响应或单位序列响应的函数形式由H()的极点确定。(c)若有r重极点,下面讨论H()极点的位置与其时域响应的函数形式。则A(2)中有因子(s+a)或[(s+a)+β2F,其响应为所讨论系统均为因果系统。K,t'e-ate (t)或K,te-atcos(B t+ e) e (0) (i-0,1,.,r-1)以上三种情况：当(→8时，响应均趋于0。暂态分量。1.连续因果系统H(9)按其极点在s平面上的位置可分为:在左半开平（2）在虚轴上面、虚轴和右半开平面三类。(a)单极点p=0或pz-±jB，则响应为Ke (t)或Kcos(Bt+ )e (t)---稳态分量（1）在左半平面(b)r重极点，相应A(s)中有sr或(s2+B2)，其响应函数为(α>0),则A(s)中有(a)若系统函数有负实单极点p=Kte(t)或K.tcos(Bt+）e(t)(i-0,1,2....,r-1)递增函数因子(s+a），其所对应的响应函数为Ke-ate（t)（3）在右半开平面：均为递增函数。2. 离散因果系统H(2)按其极点在z平面上的位置可分为:在单位圆内、增能续因果系统的(10的面数形式由H]的授应确定。型化员点的变美容量外常心单位圆外三类。①H(s)在左半平面的极点所对应的响应函数为衰减的。①H(2)在单位圆内的极点所对应的响应序列为衰减的。即当1→时，响应均趋于0。即当k→时，响应均趋于0。②H(S)在虚轴上的一阶极点所对应的响应函数为稳态分量,②H(2)在单位圆上的一阶极点所对应的响应函数为稳态国③H(s)在虚轴上的高阶极点或右半平面上的极点，其所③H(2)在单位圆上的高阶极点或单位圆外的极点，其对应的响应函数都是递增的。所对应的响应序列都是增的。即当k→0时，响应时，响应均趋于。亚均趋于

1 第七章 系统函数 § 7.1 系统函数与系统特性 一、系统函数的零、极点分布图 LTI系统的系统函数是 复变量s或z的有理分式，即 A(.)=0的根p1，p2，.，pn称为系统函数H(.)的极点； B(.)=0的根ξ1，ξ2，.，ξm称为系统函数H(.)的零点。 ( ) ( ) ( ) • • • = A B H 例：已知H(s)的零、极点分布图如示，并且h(0+)=2。求 H(s)的表达式。 σ jω -1 0 j2 -j2 解：由分布图可得 ( 1) 4 2 5 ( ) 2 2 + + = + + = s s Ks s Ks H s 根据初值定理，有 K s s Ks h sH s s s = + + + = = →∞ →∞ 2 5 (0 ) lim ( ) lim 2 2 2 5 2 ( ) 2 + + = s s s H s 二、系统函数H(·)与时域响应h(·) 冲激响应或单位序列响应的函数形式由H(.)的极点确定。 下面讨论H(.)极点的位置与其时域响应的函数形式。 所讨论系统均为因果系统。 1．连续因果系统 H(s)按其极点在s平面上的位置可分为:在左半开平 面、虚轴和右半开平面三类。 （1）在左半平面 (a)若系统函数有负实单极点p= –α(α>0)，则A(s)中有 因子(s+α)，其所对应的响应函数为Ke-αt ε(t) (b) 若有一对共轭复极点p12=-α±jβ，则A(s)中有因 子[(s+α)2+β2]-ÆK e-αt cos(βt+θ)ε(t) (c) 若有r重极点， 则A(s)中有因子(s+α)r或[(s+α)2+β2]r，其响应为 Ki ti e-αt ε(t)或Ki ti e-αt cos(βt+θ)ε(t) (i=0,1,2,.,r-1) 以上三种情况：当t→∞时，响应均趋于0。暂态分量。 （2）在虚轴上 (a)单极点p=0或p12=±jβ， 则响应为Kε(t)或Kcos(βt+θ)ε(t)-稳态分量 (b) r重极点，相应A(s)中有sr或(s2+β2)r，其响应函数为 Ki ti ε(t)或Ki ti cos(βt+θ)ε(t)(i=0,1,2,.,r-1)—递增函数 （3）在右半开平面 ：均为递增函数。 结论： LTI连续因果系统的h(t)的函数形式由H(s)的极点确定。 ①H(s)在左半平面的极点所对应的响应函数为衰减的。 即当t→∞时，响应均趋于0。 ②H(s)在虚轴上的一阶极点所对应的响应函数为稳态分量。 ③H(s)在虚轴上的高阶极点或右半平面上的极点，其所 对应的响应函数都是递增的。 即当t→∞时，响应均趋于∞。 2．离散因果系统 H(z)按其极点在z平面上的位置可分为:在单位圆内、 在单位圆上和在单位圆外三类。 根据z与s的对应关系，有结论： ①H(z)在单位圆内的极点所对应的响应序列为衰减的。 即当k→∞时，响应均趋于0。 ②H(z)在单位圆上的一阶极点所对应的响应函数为稳 态响应。 ③H(z)在单位圆上的高阶极点或单位圆外的极点，其 所对应的响应序列都是递增的。即当k→∞时，响应 均趋于∞

三、 系统函数收敏域与其极点之间的关系四、 系统函数与频率响应1连续因果系统根据收敛域的定义，H()收敛域不能含H()的极点。若系统函数H(s)的极点均在左半平面，则它在虚轴上例：某离散系统的系统函数（0)也收敏，有(0)-H()L-10,H()=403+3下面介绍两种常见的系统。(1)若系统为因果系统,求单位序列响应(k);（1）全通函数(2)若系统为反因果系统，求单位序列响应h(k)若系统的幅频响应[ H(jα)(为常数，则称为全通系统(3)若系统存在频率响应，求单位序列响应h(k);其相应的H(s）称为全通函数凡极点位于左半开平面，零点位于右半开平面解(1) [2/>3, h(k)-=[(-0.5) + (3)[8(k)并且所有零点与极点对于虚轴为一一镜像对称的系统-(2) [2/°。式中。=0T，为角频率，T为取样周期。离散因果系统的充分必要条件是；单位响应 h(k)=0,kP。（2）离散系统稳定的充分必要条件是二、 系统的稳定性2 (k)≤M1、稳定系统的定义若H(2)的收敛域包含单位圆，则该系统必是稳定的系统。一个系统，若对任意的有界输入，其零状态响应也是有界的，则称该系统是有界输入有界输出(BIBO)稳定的例1 y(k)+1.5y(k-1)-y(k-2)= (k-1)系统，简称为稳定系统。1) 若为因果系统，求h(k)，并判断是否稳定。即，若系统对所有的激励[I(-)]≤M，其零状态响应(2) 若为稳定系统，求h(k).y(.)<≤M，则称该系统稳定-03 +3- 09解 H(=)=1+1.5=-3=+（1）连续系统稳定的充分必要条件是的的的的杂,胰jih(1)] dts Mh(k)=0.4[0.5k-(-2)l e (k),(2)若为稳定系统，故收敛域为0.5<z<2，所以若H(S)的收敛域包含虚轴，则该系统必是稳定系统。h(k)=0.4(0.5)k e (k)+0.4(-2)k e (-k-1)

2 三、系统函数收敛域与其极点之间的关系 根据收敛域的定义，H(·)收敛域不能含H(·)的极点。 例：某离散系统的系统函数 0.5 3 ( ) − + + = z z z z H z (1) 若系统为因果系统，求单位序列响应h(k); (2) 若系统为反因果系统，求单位序列响应h(k); (3) 若系统存在频率响应，求单位序列响应h(k); 解 (1) |z|>3，h(k) =[(-0.5)k + (3)k]ε(k) (2) |z|σ0 离散因果系统的充分必要条件是：单位响应 h(k)=0, kρ0 二、系统的稳定性 1、稳定系统的定义 一个系统，若对任意的有界输入，其零状态响应也是有 界的，则称该系统是有界输入有界输出(BIBO)稳定的 系统，简称为稳定系统。 即，若系统对所有的激励 |f(.)|≤Mf ，其零状态响应 |yf (.)|≤My，则称该系统稳定。 （1）连续系统稳定的充分必要条件是 ∫ ∞ −∞ | h(t) | dt ≤ M 若H(s)的收敛域包含虚轴，则该系统必是稳定系统。 （2）离散系统稳定的充分必要条件是 若H(z)的收敛域包含单位圆，则该系统必是稳定的系统。 ∑ ∞ =−∞ ≤ k | h(k) | M 例1 y(k)+1.5y(k-1)-y(k-2)= f(k-1) (1) 若为因果系统，求h(k)，并判断是否稳定。 (2) 若为稳定系统，求h(k). 解 2 0.4 0.5 0.4 1 1.5 1.5 1 ( 0.5)( 2) ( ) 1 2 2 1 + − + − = − + = + − = + − = − − z z z z z z z z z z z z z H z (1)为因果系统，故收敛域为|z|>2，所以 h(k)=0.4[0.5k-(-2)k]ε(k)，不稳定。 (2)若为稳定系统，故收敛域为0.5<|z|<2，所以 h(k)=0.4(0.5)kε(k)+0.4(-2)kε(-k-1)

因果系统稳定性的充分必要条件可简化为例1：如图反馈因果系统，问当K满足什么条件时，系统是稳定的? 其中子系统的系统函数G(s)-1/[(s+1)(s+2)I(3）连续因果系统jih(t)]dtsM解：设加法器的输出信号x(S)r(因为因果系统左半开平面的极点对应的响应为衰减函数X(s)=KY(S)+F(s)O故，若H(S)的极点均在左半开平面，则该系统必是稳定的因果系统。Y(s)= G(s)X(s)=K G(s)Y(s)+ G(s)F(s)21h(k)M（4）高散因果系统H(s)-Y(S)/F($)-G(S)/[1-KG(s)-1($+3$+2-k)O的报点为完一间因为因果系防糖体竭内的极 对产的激察疾癌难源整若H(z)的极点均在单位圆内，则该系统必是稳定的因果系统。为使极点在左半平面，必须(3/2)-2+k0，不难将多项式A(s)的系数排列为如下阵列一罗斯阵列第1行 a, an-2 a- 例1 A($)=2s++$+1282+8+2第2行05注意：在排罗斯阵列第3行c.罗斯阵列：212时，可能遇到一些特由第1,2行，接下列规则计算得到;18a国ca a-- 元素全为0，这时可断言：该多项式不是第4行由2，3行同样方法得到。一直排到第n+1行。8.5尔维兹多项式。罗斯准则指出：若第一列元素具有相同的符号，则A(s)=0所有的根均在左半开平面。若第一列元素出现符号改变，则符号改变的总次数就是右半平面根的个数。第1列元素符号改变2次，因此，有2个根位于右半平面

3 因果系统稳定性的充分必要条件可简化为 （3）连续因果系统 ∫ ∞ ≤ 0 | h(t) | dt M 因为因果系统左半开平面的极点对应的响应为衰减函数。 故，若H(s)的极点均在左半开平面，则该系统必是稳定 的因果系统。 （4）离散因果系统 因为因果系统单位圆内的极点对应的响应为衰减函数。 故，若H(z)的极点均在单位圆内，则该系统必是稳定 的因果系统。 ∑ ∞ = ≤ 0 | ( ) | k h k M 例1：如图反馈因果系统，问当K满足什么条件时，系 统是稳定的？其中子系统的系统函数G(s)=1/[(s+1)(s+2)] 解：设加法器的输出信号X(s) ∑ G(s) K F(s) Y(s) X(s) X(s)=KY(s)+F(s) Y(s)= G(s)X(s)=K G(s)Y(s)+ G(s)F(s) H(s)=Y(s)/F(s)=G(s)/[1-KG(s)]=1/(s2+3s+2-k) H(s)的极点为 p  − + k      = − ± 2 2 3 2 3 2 1,2 为使极点在左半平面，必须(3/2)2-2+k0，不难 得出，A(s)为霍尔维兹多项式的条件为：a1>0，a0>0 例1 A(s)=2s4+s3+12s2+8s+2 罗斯阵列： 2 12 2 1 8 0 4 1 1 8 2 12 − = − 2 8.5 0 2 第1列元素符号改变2次，因此，有2个根位于右半平面。 注意：在排罗斯阵列 时，可能遇到一些特 殊情况，如第一列的 某个元素为0或某一行 元素全为0，这时可断 言：该多项式不是霍 尔维兹多项式

四、 离散因果系统稳定性判断准则-朱里准则例2 已知某因果系统函数为判断高散因果系统的稳定性，要判断A(Z)-0的所有H()=7+3* +35+1+k根的绝对值是否都小于1。朱里提出一种列表的检验方法，称为朱里准则为使系统稳定，k应满足什么条件？朱里列表：第1行解 列罗斯阵列1+k第2行In-2an-1a第3行(8-k)/3第4行Ca-t1+k官5行d.d第6行所以，-10 (-1)A(-1)-5>0ega.a.a..排朱里列表一直到第2m-3行，该行有3个元素。朱里准则指出，A(2)-0的所有根都在单位圆内的充分必要24152-104的条件是： (1)A(1)>0(2) (-1)"A(-1)>01-14(3) a,>laol. cn->/col d-2>/d.l>奇数行，其第1完素必大于最后一不元素的绝对值。特例: 对二阶系统。 A(2)=,+;,2+a,易得所以系统稳定。209>5615>4,A(1)>0 A(-1)>0 a,>/a87.3信号流图(1)结点：信号流图中的每个结点表示一个变量或信号。用方框图描述系统的功能比较直观。信号流图是用在的和高之的有的腺称为变。有向的线图描述方程变量之间因果关系的一种图，用它描述系统比方框图更加简便。信号流图首先由每条支路上的权值（支路增益）就是该两结点间的系统Mason于1953年提出的，应用非常广泛，函数（转移函数）信号流图就是用一些点和有向线段来描述系统，与H(s)-0 Y(s)框图本质是一样的，但简便多了。F(s) 0一、 信号流图即用一条有向线段表示一个子系统。、定义：信号流图是由结点和有向线段组成的几何图(3)源点与汇点，混合结点：形。它可以简化系统的表示，并便于计算系统函激。仅有出支路的结点称为源点（或输入结点）。仅有入支路的结点称为汇点（或输出结点）。2、信号流图中常用术语有入有出的结点为混合结点

4 例2 已知某因果系统函数 s s s k H s + + + + = 3 3 1 1 ( ) 3 2 为使系统稳定，k应满足什么条件？ 解 列罗斯阵列 1 3 3 1+k (8-k)/3 1+k 所以， –10 (2) (-1)nA(-1)>0 (3) an>|a0| cn-1>|c0| dn-2>|d0| . r2>|r0| 奇数行，其第1个元素必大于最后一个元素的绝对值。 特例：对二阶系统。A(z)=a2z2+a1z+a0,易得 A(1)>0 A(-1)>0 a2>|a0| 例 A(z)=4z4-4z3+2z-1 解 4 -4 0 2 -1 -1 2 0 -4 4 15 -14 0 4 4 0 -14 15 209 -210 56 4>1 ， 15>4 ， 209>56 所以系统稳定。 (-1)4A(-1)=5>0 排朱里列表 A(1)=1>0 § 7.3 信号流图 用方框图描述系统的功能比较直观。信号流图是用 有向的线图描述方程变量之间因果关系的一种图，用 它描述系统比方框图更加简便。信号流图首先由 Mason于1953年提出的，应用非常广泛。 信号流图就是用一些点和有向线段来描述系统，与 框图本质是一样的，但简便多了。 一、信号流图 1、定义：信号流图是由结点和有向线段组成的几何图 形。它可以简化系统的表示，并便于计算系统函数。 2、信号流图中常用术语 (1)结点： 信号流图中的每个结点表示一个变量或信号。 (2)支路和支路增益： 连接两个结点之间的有向线段称为支路。 每条支路上的权值（支路增益）就是该两结点间的系统 函数（转移函数） F(s) H(s) Y(s) 即用一条有向线段表示一个子系统。 (3)源点与汇点，混合结点： 仅有出支路的结点称为源点（或输入结点）。 仅有入支路的结点称为汇点（或输出结点）。 有入有出的结点为混合结点

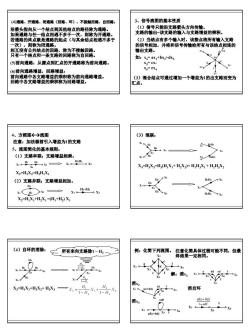
3、信号流图的基本性质（4)通路、开通路、闭通路（回路、环）、不接触回路、自回路（1）信号只能沿支路箭头方向传输。沿箭头指向从一一个结点到其他结点的路径称为通路。支路的输出-该支路的输入与支路增益的乘积。结点相遇不多一（2）当结点有多个输入时，该接点将所有输入支路若通路的终点就是通路的起点（与其余结点相遇不多于一次），则称为闭通路的信号相加，并将和信号传输给所有与该结点相连的输出支路。相互没有公共结点的回路，称为不接触回路。WA只有一个结点和一条支路的回路称为自回路如: x,= ax,+bx+dxsNe(5)前向通路：从源点到汇点的开通路称为前向通路。bXg=cxX-ex(6)前向通路增益，回路增益；称为前向通路增益。前向通路中务支略增益的(3）混合结点可通过增加一个增益为1的出支路而变为回路中各支路增益的乘积称为回路增益。点。4、方框图←→流图(3)混联：注意：加法器前引入增益为1的支路XOEE5、流图简化的基本规则：（1）支路申联：支路增益相乘。1HiHXoHX-H,X,-H(H,X+ H,X2)-H,H,XI+H,H,XX,-H,X,-I,H,x,1（2）支路并联：支路增益相加。XioHi+H2XCDxYoUX,-H,X,+H,X, =(H,+H,) X,（4）自环的消除：所有来向支路除1-H例：化简下列流图。化简具体过程可能不同，但最I"x/uK1X-H,X,+HX2+ HX消自环X+I-HX"1-Haf(c+ba)消xKroafsthd)

5 沿箭头指向从一个结点到其他结点的路径称为通路。 如果通路与任一结点相遇不多于一次，则称为开通路。 若通路的终点就是通路的起点（与其余结点相遇不多于 一次），则称为闭通路。 相互没有公共结点的回路，称为不接触回路。 只有一个结点和一条支路的回路称为自回路。 (5)前向通路：从源点到汇点的开通路称为前向通路。 (6)前向通路增益，回路增益： 前向通路中各支路增益的乘积称为前向通路增益。 回路中各支路增益的乘积称为回路增益。 (4)通路、开通路、闭通路（回路、环）、不接触回路、自回路： 3、信号流图的基本性质 （1）信号只能沿支路箭头方向传输。 支路的输出=该支路的输入与支路增益的乘积。 （2）当结点有多个输入时，该接点将所有输入支路 的信号相加，并将和信号传输给所有与该结点相连的 输出支路。 x1 x2 x3 x4 x5 x6 a b c d e 如：x4= ax1+bx2+dx5 x3= cx4 x6= ex4 （3）混合结点可通过增加一个增益为1的出支路而变为 汇点。 4、方框图ÅÆ流图 注意：加法器前引入增益为1的支路 5、流图简化的基本规则： （1）支路串联：支路增益相乘。 X1 X3 X2 H1 H2 X2=H2X3=H2H1X1 X1 X2 H1H2 （2）支路并联：支路增益相加。 X1 X2 H1 H2 X2=H1X1+H2X1 =(H1+H2) X1 X1 X2 H1+H2 （3）混联： X1 H1 X H2 2 H3 X3 X4 X4=H3X3=H3(H1X1+ H2X2)= H1H3X1 + H2H3X2 X1 X2 X4 H1H3 H2H3 X1 X2 X3 X4 H1 H2 H3 X1 X3 X4 H1H2 H1H3 （4）自环的消除： X1 X2 X3 X4 H1 H2 H3 H4 X3=H1X1+H2X2+ H3X3 2 3 2 1 3 1 3 1 1 X H H X H H X − + − = X1 X2 X3 X4 H4 3 1 1 H H − 3 2 1 H H − 所有来向支路除1 – H3 例：化简下列流图。 X1 X2 X3 X4 X5 X6 a b c d e f 1 注意化简具体过程可能不同，但最 终结果一定相同。 解：消x3 X1 X2 X4 X5 X6 a c f bd ed 1 消x2 X1 X4 X5 X6 f 1 a(c+bd) ed 消x4 af(c+bd) edf 1 X1 X5 X6 消自环 1 X1 X5 X6 1 edf af(c bd) − +

二、梅森公式上述化简求H复杂。利用Mason公式方便。例求下列信号流图的系统函数系统函数H(.)记为H。梅森公式为：H=解(1)首先找出所有回路：-EPAL,=H,GA-1-ZL,+ZL-ZL,+称为信号流图的特L,-2H,H,H,H,正行刻式L,-H,H,H,,为所有不同回路的增益之和；(2)求特征行列式≥L1。 为所有两两不接触回路的增益乘积之和;A-1- (H,G+2H,H,H,H,+H,H,H,) +H,G H,H,H,≥L,。 为所有三三不接触回路的增益乘积之和..(3)然后找出所有的前向通路：H=-(PA, +P2A2)P,=2H,H,H,1表示由源点到汇点的第i条前向通路的标号P,-H,HP,是由源点到汇点的第i条前向通路增益；(4)求各前向通路的余因子：△,=1，A,=1-GH,△,称为第条前向通路特征行列式的余因子。消去接触回路二、级联实现s7.4系统模拟将H分解为若干简单（一阶或二阶子系统）的系统函数的乘积，即H-HH,.HMason公式是由流图→H(S)或H(2)一、 二阶子系统函数下面讨论，由H(s)或H(2)流图或方框图1+b,=*" +ba-H,(2)=I+a- H()-10-+0一、直接实现-利用Mason公式来实现5s2+5ss2+5三、并联实现例HO-0-0将展开成部分分式，将每个分式分别进行模拟，然后将它们并联起来。分子中每项看成是一条前向通路。分母中，除1之外5($+1)_1/2,5/6-4/3其余每项看成回路。画流图时，所有前向通路与全H(0- +5-2-5部回路相接触。所有回路均相接触例 H(s)=小结2(s+ 2)Os-s+5+7+3*+58+3($+1Xs*+28+3)$+1,+28+3$+1++25+3系统特性：系统函数的零极点,时域、频域响应系统的稳定性：连续系统-罗斯准则，离散系统-朱里准则信号流图：梅森公式系统模拟：直接实现，级联和并联实现

6 二、梅森公式 上述化简求H复杂。利用Mason公式方便。 系统函数H(.)记为H。梅森公式为： ∑ ∆ ∆ = i H p i i 1 ∆ = −∑ + ∑ − ∑ +" p q r p q r m n m n j Lj L L L L L , , , 1 称为信号流图的特 征行列式 ∑ 为所有不同回路的增益之和； j Lj ∑ m n Lm Ln , 为所有两两不接触回路的增益乘积之和； ∑p q r LpLqLr , , 为所有三三不接触回路的增益乘积之和；. i 表示由源点到汇点的第i条前向通路的标号 Pi 是由源点到汇点的第i条前向通路增益； △i 称为第i条前向通路特征行列式的余因子 。消去接触回路 例 求下列信号流图的系统函数 H4 1 H1 H2 H3 2 1 G H5 解 (1)首先找出所有回路： L1=H3G L2=2H1H2H3H5 L3=H1H4H5 (2)求特征行列式 △=1-（H3G+2H1H2H3H5+ H1H4H5）+ H3G H1H4H5 (4)求各前向通路的余因子：△1 =1 ， △2 =1-GH3 (3)然后找出所有的前向通路： p1=2H1H2H3 p2=H1H4 ( ) 1 1∆1 + 2∆2 ∆ H = p p § 7.4 系统模拟 Mason公式是由流图 Æ H(s)或H(z) 下面讨论，由H(s)或H(z) Æ 流图或方框图 一、直接实现-利用Mason公式来实现 例 1 [ 7 10 ] 5 5 1 7 10 5 5 7 10 5 5 ( ) 1 2 2 3 1 2 2 3 3 2 − − − − − − − − − − − + = + + + = + + + = s s s s s s s s s s s s H s 分子中每项看成是一条前向通路。分母中，除1之外， 其余每项看成一个回路。画流图时，所有前向通路与全 部回路相接触。所有回路均相接触。 二、级联实现 将H分解为若干简单（一阶或二阶子系统）的系统 函数的乘积，即 H=H1H2.Hn 一、二阶子系统函数 1 0 1 0 1 1 ( ) − − + + = a z b z H z i i i 2 0 1 1 2 0 1 1 1 1 ( ) − − − − + + + + = a z a z b z b z H z i i i i i 三、并联实现 将H展开成部分分式，将每个分式分别进行模拟，然 后将它们并联起来。 5 4 / 3 2 1/ 2 5 / 6 ( 2)( 5) 5( 1) ( ) + − + = + + + + = s s s s s s s H s 例 2 3 1 1 1 2 3 2 1 2 ( 1)( 2 3) 2( 2) 3 5 3 2 4 3 2 2 2 2 + + − + + + = + + + + = + + + + = + + + + s s s s s s s s s s s s s s s s H(s)= 小结 系统特性:系统函数的零极点,时域、频域响应 系统的稳定性： 连续系统-罗斯准则，离散系统-朱里准则 信号流图：梅森公式 系统模拟：直接实现，级联和并联实现