《电路》课程教学资源（PPT课件）第3章 电阻电路的一般分析

第三章 电阻电路的一投分析

第三章 电阻电路的一般分析

第3章 线性电阻电路的一般分析方法 ◆重点： 1.熟练掌握电路方程的列写方法： 支路电流法 回路电流法 节点电压法 2.掌握含运算放大器的电路的分析方法

第3章 线性电阻电路的一般分析方法  重点： 1. 熟练掌握电路方程的列写方法： 支路电流法 回路电流法 节点电压法 2. 掌握含运算放大器的电路的分析方法

第三章电阻电路的一般分析方法 §3.1基本概念 3.1.1电路的图 3.1.2KCL和KVL的独立方程数 §3.2基本方法 3.2.1支路电流法 3.2.2网孔电流法 3.2.3回路电流法 3.2.4结点电压法

第三章 电阻电路的一般分析方法 §3.1 基本概念 3.1.1 电路的图 3.1.2 KCL和KVL的独立方程数 §3.2 基本方法 3.2.1 支路电流法 3.2.2 网孔电流法 3.2.3 回路电流法 3.2.4 结点电压法

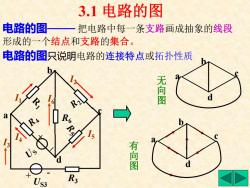
3.1电路的图 电路的图 把电路中每一条支路画成抽象的线段 形成的一个结点和支路的集合。 电路的图只说明电路的连接特点或拓扑性质 无向图 d 有向图 Us3 R3

3.1 电路的图 电路的图—— 把电路中每一条支路画成抽象的线段 形成的一个结点和支路的集合。 US3 - + R3 R6 I2 I5 I6 I1 I4 I3 a b c d a b c d 无 向 图 有 向 图 a b c d 电路的图只说明电路的连接特点或拓扑性质

3.2KVL,KCL的独立方程数 问题的提出：在用基尔霍夫电流定律或电压定 律列方程时，究竟可以列出多少个独立的方程？ 例 分析以下电路中应列几个电流方程？几个 电压方程？ #2 s2 #3 b

3.2 KVL,KCL的独立方程数 问题的提出：在用基尔霍夫电流定律或电压定 律列方程时，究竟可以列出多少个独立的方程？ 例 a I1 I2 US2 + - R1 R3 R2 + I _ 3 #1 #2 #3 b US1 分析以下电路中应列几个电流方程？几个 电压方程？

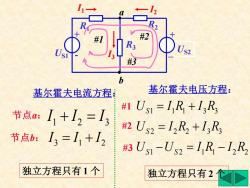
#3 b 基尔霍夫电流方程： 基尔霍夫电压方程： 节点m:1+I2=I3 #1Us1=1R+13R #2Us2=12R2+3R 节点b:I3=1+2 #3Us1-Us2=1R-12R, 独立方程只有1个 独立方程只有2有

基尔霍夫电流方程： 节点a： 节点b： 1 2 3 I + I = I 3 1 2 I = I + I 独立方程只有 1 个 基尔霍夫电压方程： #1 #2 #3 1 2 1 1 2 2 2 2 2 3 3 1 1 1 3 3 U U I R I R U I R I R U I R I R S S S S − = − = + = + 独立方程只有 2 个 a I1 I2 US2 + - R1 R3 R2 + I _ 3 #1 #2 #3 b US1

几个基本概念： 图G的路径-从图G的某一结点出发，沿着一些支路移 动，到达另一结点，所经过的一系列支路 闭合路径-从图的某一结点出发，沿着一些支路移动， 回到原出发点，所经过的一系列支路 连通图-图G的任两结点间至少存在一条路径 树T-是连通图G的一个连通子图，它包含G的全部结点 ,但不形成回路。 (设图G有n个结点，b条支路) 树支-组成树的支路，共有n-1个。 连支-连通图G除树支外的其他支路，共有b一门+1个

几个基本概念： 图G的路径-从图G的某一结点出发，沿着一些支路移 动，到达另一结点，所经过的一系列支路 闭合路径-从图的某一结点出发，沿着一些支路移动， 回到原出发点，所经过的一系列支路 连通图-图G的任两结点间至少存在一条路径 树T-是连通图G的一个连通子图，它包含G的全部结点 ，但不形成回路。 树支-组成树的支路，共有n-1个。 连支-连通图G除树支外的其他支路，共有b-n+1个。 （ 设图G有n个结点， b条支路）

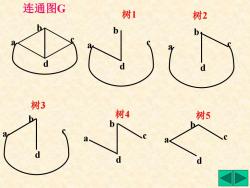
连通图G 树1 树2 d 树3 树4 树5 a

连通图 G a b c d 树 1 a b c d a b c d 树2 树 3 a b c d 树 4 a b c d 树 5 a b c d

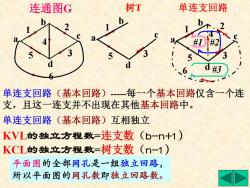
连通图G 树T 单连支回路 d d#3 单连支回路（基本回路）-每一个基本回路仅含一个连 支，且这一连支并不出现在其他基本回路中。 单连支回路（基本回路）互相独立 KVL的独立方程数=连支数(b-n+1) KCL的独立方程数=树支数（n-1) 平面图的全部网孔是一组独立回路， 所以平面图的网孔数即独立回路数

连通图G a b c d 1 2 3 4 5 6 单连支回路（基本回路）-每一个基本回路仅含一个连 支，且这一连支并不出现在其他基本回路中。 KVL的独立方程数=连支数（b-n+1） KCL的独立方程数=树支数（n-1） 单连支回路（基本回路）互相独立 平面图的全部网孔是一组独立回路， 所以平面图的网孔数即独立回路数。 树T a b c d 1 5 3 单连支回路 #1 #2 #3 2 4 6 a b c d 1 5 3

平面电路：可以画在平面上，不出现支路交叉的电路。 非平面电路：在平面上无论将电路怎样画，总有支 路相互交叉。 → ∴。是平面电路 平面电路KVL的独立方程数=网孔数(b-n+1) 总有支路相互交叉 是非平面电路

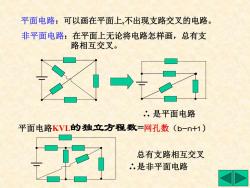
平面电路：可以画在平面上,不出现支路交叉的电路。 非平面电路：在平面上无论将电路怎样画，总有支 路相互交叉。 ∴ 是平面电路 总有支路相互交叉 ∴是非平面电路 平面电路KVL的独立方程数=网孔数（b-n+1）