《数字信号处理》课程教学课件（PPT讲稿）ch7-2 有限字长效应

有限字长效应问题的提出截尾和舍入效应滤波器输入信号量化效应滤波器系数量化效应数字滤波器的定点运算误差

有限字长效应 ◼ 问题的提出 ◼ 截尾和舍入效应 ◼ 滤波器输入信号量化效应 ◼ 滤波器系数量化效应 ◼ 数字滤波器的定点运算误差

问题的提出数字系统，存储单元的容量有限有限字长的影响，主要表现在以下三方面(1)车输入信号经A/D变换而产生的量化误差。滤波器的系数量化误差(2)运算误差。(3)

问题的提出 (1) 输入信号经A/D变换而产生的量化误 差。 (2) 滤波器的系数量化误差。 (3) 运算误差。 数字系统，存储单元的容量有限。 有限字长的影响，主要表现在以下三方面

截尾和舍入效应定点二进制数的表示量化及量化误差

截尾和舍入效应 ◼ 定点二进制数的表示 ◼ 量化及量化误差

一、定点二进制数的表示定点二进制数x有原码、反码和补码三种表示形式若x=0.XiX2Xb，则其原码、反码和补码分别定义为0≤x<1X=0.X,X2..X[]原 = {1- = X,X2 ,-1≤x<00≤x<1x= 0.X,X2:: Xb[x]反 中[1- x= 1.XiX2 ... X,-1≤x<00≤x<1x[]补=2 + x-1≤x<0

一、定点二进制数的表示 定点二进制数x有原码、反码和补码三种表示形式    − = −   =   = 1 1. 1 0 0. 0 1 [ ] 1 2 1 2 x X X X x x X X X x x b b   原    − = −   =   = 1 1. 1 0 0. 0 1 [ ] 1 2 1 2 x X X X x x X X X x x b b   反    + −     = 2 1 0 0 1 [ ] x x x x x 补 若x=0.X1 X2  Xb，则其原码、反码和补码分别定义为

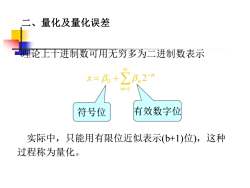
二、量化及量化误差一理论上十进制数可用无穷多为二进制数表示x= βo +β,2-nn=l有效数字位符号位实际中，只能用有限位近似表示(b+1)位)，这种过程称为量化

二、量化及量化误差 理论上十进制数可用无穷多为二进制数表示   = − = + 1 0 2 n n n x   符号位 有效数字位 实际中，只能用有限位近似表示(b+1)位)，这种 过程称为量化

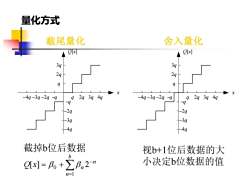
量化方式截尾量化舍入量化Q[x]Q[网]3q3q2q2qqqxX-4g-3q-2g -q2q3g4q2q3q4qq-4q-3q-2 -qa-q-q-2q-2q-3q-3q-4g4q截掉b位后数据视b+1位后数据的大b小决定b位数据的值Q[x] = βo +Zβn2-nn=1

量化方式 q −q 2q −2q 3q 4q −3q q 2q 3q −4q −4q −3q −2q −q x Q[x] q −q 2q −2q 3q 4q −3q q 2q 3q −4q −4q −3q −2q −q x Q[x] 截尾量化 舍入量化  = − = + b n n n Q x 1 [ ]  0  2 截掉b位后数据 视b+1位后数据的大 小决定b位数据的值

量化误差截尾误差Er =Q[x]-x正数和补码负数截尾误差范围为q = 2-b-q<E≤0原码负数和反码负数截尾误差范围为0E≤q舍入误差范围-q/2≤ER≤g/2区别：舍入误差对称分布，截尾误差单极性分布

量化误差 截尾误差 E Q x x T = [ ]− 舍入误差范围 − q 2  ER  q 2 正数和补码负数截尾误差范围为 − q  ET  0 原码负数和反码负数截尾误差范围为 0  ET  q 区别：舍入误差对称分布，截尾误差单极性分布。 b q − = 2

滤波器输入信号量化效应问题的提出量化误差统计假设信噪比和字长的关系

滤波器输入信号量化效应 ◼ 问题的提出 ◼ 量化误差统计假设 ◼ 信噪比和字长的关系

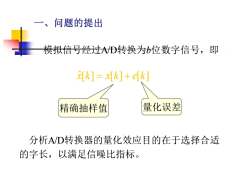
一、问题的提出模拟信号经过A/D转换为b位数字信号，即x[k]= x[k]+e[k]量化误差精确抽样值分析AVD转换器的量化效应目的在于选择合适的字长，以满足信噪比指标

一、问题的提出 模拟信号经过A/D转换为b位数字信号，即 x ˆ[k] = x[k] + e[k] 精确抽样值 量化误差 分析A/D转换器的量化效应目的在于选择合适 的字长，以满足信噪比指标

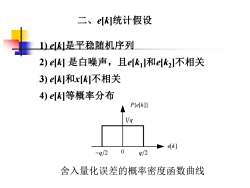
二、e[k]统计假设1)e[kl是平稳随机序列2)e[k] 是白噪声，且e[k]和e[k,]不相关3) e[k]和x[k]不相关4)e[kl等概率分布P(e[k])1/ qe[k]0q/2-q/2舍入量化误差的概率密度函数曲线

二、e[k]统计假设 1) e[k]是平稳随机序列 2) e[k] 是白噪声，且e[k1 ]和e[k2 ]不相关 3) e[k]和x[k]不相关 4) e[k]等概率分布 e[k] P{e[k]} 1 q −q 2 0 q 2 舍入量化误差的概率密度函数曲线