《数字信号处理》课程教学课件（PPT讲稿）ch1_6 系统函数

离散系统z域分析·系统函数H(z）·差分方程和系统函数·系统函数H（z）的表示方式·用MATLAB转换不同表示形式的系统函数·简单数字滤波器

离散系统z域分析 •系统函数H(z) •差分方程和系统函数 •系统函数H(z)的表示方式 •用MATLAB转换不同表示形式的系统函数 •简单数字滤波器

系统函数（transferfunction,systemfuncti对LTI系统：y[k]=x [K]*h[K]由z变换的性质：Y(z)=H(z)X(z)H(2)称为离散LTI系统的系统函数当的H)ROC包含单位圆时H(ej°)= H(z)z =ejQ是h[k实系数时，由H(ej)的对称性质可得H(ej)" = H(ej?)H*(ej?)= H(ej?)H(e-j?)= H(z)H(z-")=

系统函数(transfer function,system function) 对LTI系统: y[k]=x [k]*h[k] 由z变换的性质：Y(z)=H(z)X(z) H(z)称为离散LTI系统的系统函数   = = j j H(e ) H(z) z e 当的H(z) ROC包含单位圆时 是h[k]实系数时，由H(e j)的对称性质可得 ( ) ( ) ( ) 2     = j j j H e H e H e ( ) ( )  −  = j j H e H e  = − = j z e H(z)H(z ) 1

差分方程和系统函数MNZany[k-n]=Zb,x[k-n]n=0n=0MZb.Y(z)n=0H()>WX(2)na.znn=0N=O,ao#0 时，系统称FIR(finite impulse response)N>0，(ak;k=1,2...N中至少有一项非零时，系统被称为IR(infinite impulseresponse)系统

差分方程和系统函数 [ ] [ ] 0 0 a y k n bn x k n M n n N n  − =  − = = n n N n n n M n a z b z X z Y z H z − = − =   = = 0 0 ( ) ( ) ( ) N=0, a00 时，系统称FIR(finite impulse response) N>0，{ak ;k=1,2.N}中至少有一项非零时，系统被称 为IIR(infinite impulse response)系统

系统函数H(z）的表示方式a)z1的有理函数表示7-Mbo +b,z-1 +..H(z) :VZ-Mao +az- +...+ab)z的有理函数表示1++H(2)= z(N-M) b+...+an

系统函数H(z)的表示方式 a) z -1的有理函数表示 N N M M a a z a z b b z b z H z − − − − + + + + + + =   1 0 1 1 0 1 ( ) b) z的有理函数表示 N N N M M M N M a z a z a b z b z b H z z + + + + + + = − − −   1 0 1 1 ( ) 0 1 ( )

c)零点、极点和增益常数表示(z - z(1)(z - z(2) .: ·(z - z(M))H(z)= kz(N-M)(z- p(1)(z - p(2)) . . :(z- p(N)d)2阶因子表示Lbok +bkz-1 + bakzH(2)=IIaok +aikz-l +a,k=11

c)零点、极点和增益常数表示 ( (1))( (2)) ( ( )) ( (1))( (2) ( ( )) ( ) ( ) z p z p z p N z z z z z z M H z k z N M − − − − − − = −   d) 2阶因子表示 2 2 1 0 1 2 2 1 0 1 1 ( ) − − − − = + + + + = a a z a z b b z b z H z k k k k k k L k

用MATLAB转换不同表示形式的系统函数[zp,k=tf2zp(ba)将z的有理函数表示转换为零点、极点和增益常数表示，[b,a]=zp2tf(z,p,k)将零点、极点和增益常数表示转换为有理函数表示(second-ordersection)sos=zp2sos(z,p,k)将零点、极点和增益常数表示转换为2阶因子表示[bo bi b21a21ao1anb22bo2 bi2 ao2a12a22SOS =:.:学boLbb2LarlaoLa2L

[z,p,k]=tf2zp(b,a) 将z的有理函数表示转换为零点、极点和增益常数表示。 [b,a]=zp2tf(z,p,k) 将零点、极点和增益常数表示转换为有理函数表示。 sos=zp2sos(z,p,k) (second-order section) 将零点、极点和增益常数表示转换为2阶因子表示             = b L b L b L a L a L a L b b b a a a b b b a a a 0 1 2 0 1 2 0 2 1 2 2 2 0 2 1 2 2 2 0 1 1 1 2 1 0 1 1 1 2 1 sos       用MATLAB转换不同表示形式的系统函数

例试求下面系统函数的零极点形式2阶因子形式z3 +0.04zH(2)=7 -0.82 +0.16z-0.128Determination of thefactored form and%the second order section form ofa% rational z-transform01;b=[100.04a=[1-0.80.16-0.1281;[z,p,k]=tf2zp(b,a);disp('zeros are at'); disp(z);disp('Poles are at'); disp(p);disp('Gainconstant');disp(k);sos=zp2sos(z,p,k);disp('Second-order sections);disp(real(sos));

例 试求下面系统函数的零极点形式2阶因子形式。 %Determination of the factored form and %the second order section form of a % rational z-transform b =[1 0 0.04 0]; a =[1 -0.8 0.16 -0.128]; [z,p,k]=tf2zp(b,a); disp('Zeros are at'); disp(z); disp('Poles are at'); disp(p); disp('Gain constant');disp(k); sos=zp2sos(z,p,k); disp('Second-order sections'); disp(real(sos)); 0.8 0.16 0.128 0.04 ( ) 3 2 3 − + − + = z z z z z H z

程序的运行结果为Zeros are at00+0.2000i0-0.20001Poles are at0.80000.0000+04000i0.0000-0.40001Gain constant1z(z - 0.2 j)(z + 0.2 j)H(z) :(z - 0.8)(z - 0.4 j)(z + 0.4 j)Second-order sections0000.20001.0000-0.800005.00000.20001.00000.00000.16001 + 0.04z-20.2(5 +0.2z-2)H(z) =(1-0.8z-')(1 +0.16z-2)(1-0.8z-')(1+0.16z-2)

程序的运行结果为 Zeros are at 0 0 + 0.2000i 0 - 0.2000i Poles are at 0.8000 0.0000 + 0.4000i 0.0000 - 0.4000i Gain constant 1 ( 0.8)( 0.4 )( 0.4 ) ( 0.2 )( 0.2 ) ( ) z z j z j z z j z j H z − − + − + = Second-order sections 0.2000 0 0 1.0000 -0.8000 0 5.0000 0 0.2000 1.0000 0.0000 0.1600 (1 0.8 )(1 0.16 ) 0.2(5 0.2 ) ( ) 1 2 2 − − − − + + = z z z H z (1 0.8 )(1 0.16 ) 1 0.04 1 2 2 − − − − + + = z z z

用MATLAB画画出平面的零极点分布zplane(b,a)b,a：正幂表示的分子和分母多项式例已知一离散因果的LTI系统的系统函数为z3 +2z? + zH(2)= -0.522 -0.005z +0.3%zerosand poles of the transfer functionb=[12101;-0.50.31 ;a=[1-0.005[h1,h2]=zplane(b,a);set(h2,'markersize',8,'color',[100]);

用MATLAB画画出z平面的零极点分布 zplane(b,a) b,a :正幂表示的分子和分母多项式 例 已知一离散因果的LTI系统的系统函数为 0.5 0.005 0.3 2 ( ) 3 2 3 2 − − + + + = z z z z z z H z %zeros and poles of the transfer function b =[1 2 1 0]; a =[1 -0.5 -0.005 0.3]; [h1,h2]=zplane(b,a); set(h2,'markersize',8,'color',[1 0 0]);

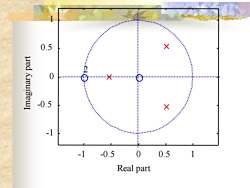
0.5+ -0.50-1-0.50.5Real part

- 1 -0.5 0 0.5 1 - 1 -0.50 0.51 Real part Imaginary part 2