《数字信号处理》课程教学资源（教案讲义）ch1 离散信号与系统分析基础

第一章离散信号与系统分析基础●离散时间信号与系统●离散时间信号的频域分析●离散系统的频域分析●双边z变换●系统函数●全通滤波器与最小相位系统信号的抽样1.1离散时间信号与系统离散信号(序列)的表示离散序列的产生常用序列序列的基本运算系统分类单位脉冲响应用MATLAB求解离散LTI系统响应离散信号（序列）的表示2[]0-1-1x[K]=(1, 1, 2, -1, 1;k=-1,0,1,2,3]

第一章 离散信号与系统分析基础 ●离散时间信号与系统 ●离散时间信号的频域分析 ●离散系统的频域分析 ●双边 z 变换 ●系统函数 ●全通滤波器与最小相位系统 ●信号的抽样 1.1 离散时间信号与系统 离散信号(序列)的表示 离散序列的产生 常用序列 序列的基本运算 系统分类 单位脉冲响应 用 MATLAB 求解离散 LTI 系统响应 离散信号(序列)的表示 x [k]={1, 1, 2, -1, 1;k=-1,0,1,2,3} k 1 2 1 -1 -1 0 1 2 3 x[k] 1

离散序列的产生1)对连续信号抽样x[k]=x(k7)，T-samplingperiod2）信号本身是离散的3)计算机产生离散信号：时间上都量化的信号数字信号：时间和幅度上都量化的信号1.1.1 常用序列1.单位脉冲序列k=0o[k]=l0k±02.单位阶跃序列1k≥01u[k] =0k<03.矩形序列0≤k≤N-1R[k]=0otherwise4.指数序列x[k]=a,kez有界序列：VkeZx[K]l≤Mx,Mx是与k无关的常数aku[k]:右指数序列,la≤1序列有界au[-k]：左指数序列, lal|≥1 序列有界5.正弦型序列x[k]= cos k2=(ejk +e-ja)/2例试确定余弦序列x[K]=cos。k当(a)2。=0(b)2.=0.1元(c)2。=0.2元(d)2。=0.8元(e) 2。=0.9元时的基本周期。(f) 2.=元解：N=l。(a)2。/2元=0/1

离散序列的产生 1)对连续信号抽样 x[k]=x(kT) , T-sampling period 2) 信号本身是离散的 3)计算机产生 离散信号: 时间上都量化的信号 数字信号: 时间和幅度上都量化的信号 1.1.1 常用序列 1．单位脉冲序列     = = 0 0 1 0 [ ] k k  k 2.单位阶跃序列      = 0 0 1 0 [ ] k k u k 3．矩形序列      − = 0 otherwise 1 0 1 [ ] k N R k N 4．指数序列 有界序列： kZ |x [k]|  Mx ,Mx 是与 k 无关的常数 a ku[k]： 右指数序列, |a| 1 序列有界 a ku[-k]： 左指数序列, |a| 1 序列有界 5.正弦型序列 例 试确定余弦序列 x[k] = cos 0 k 当(a) 0 =0 (b) 0 =0.1  (c) 0 =0.2  (d) 0 =0.8  (e) 0 =0.9  (f) 0= 时的基本周期。 解： (a) 0 /2  = 0/1， N=1。 [ ] cos ( )/ 2 j k j k x k k e e    − = = + x k = a k  Z k [ ]

(b) 2。 /2 元=0.1/2=1/20,N=20。N=10。(c2。/2元=0.2/2=1/10,N=5。(d）2。/2元=0.8/2=2/5,N=20。(e)2。/2元=0.9/2=9/20N=2。(f) 2,/2 元=1/2,cos[(2p-Q2。 )k]=cos(。 k)当2。从元增加到2元时，余弦序列幅度的变化将会逐渐变慢。2。在元附近的余弦序列是高频信号。2。在0或2元附近的余弦序列是低频信号。cos(2 +2πn)k)=cos(2k) neZ即两个余弦序列的角频率相差2元的整数倍时，所表示的是同一个序列。6.虚指数序列(单频序列)x(t)=ej角频率为的模拟信号[k]= x(t) (=kr =ejo7k =ejak数字信号角频率Q=TW虚指数序列x[K]=exp(jk）是否为周期的?如是周期序列其周期为多少？即2/2p为有理数时，信号才是周期的。如果Q/2p=m/L，L,m是不可约的整数，则信号的周期为L。用MATLAB产生序列MATLAB中的基本函数：exp，sin，cos，square,sawtooth例用MATLAB产生指数序列x[K]=Kaku[K]a=input(输入指数 a=");K=input(输入常数K=");N=input（输入序列长度N=")k=0.N;x=K*a.k;stem(k,x);xlabel(时间);ylabel(幅度）title([lalpha =,num2str(a);

(b) 0 /2  =0.1/2=1/20， N=20。 (c) 0 /2  =0.2/2=1/10， N=10。 (d) 0 /2  =0.8/2=2/5， N=5。 (e) 0 /2  =0.9/2=9/20, N=20。 (f) 0 /2  =1/2, N=2。 cos[(2p-0 )k]= cos( 0 k) 当 0 从  增加到 2  时，余弦序列幅度的变化将会逐渐变慢。 0 在  附近的余弦序列是高频信号。 0 在 0 或 2  附近的余弦序列是低频信号。 即两个余弦序列的角频率相差 2  的整数倍时， 所表示的是同一个序列。 6.虚指数序列(单频序列) 角频率为  的模拟信号 数字信号角频率  =T w 虚指数序列 x [k]=exp( j  k) 是否为周期的?如是周期序列其 周期为多少？ 即  / 2p 为有理数时，信号才是周期的。 如果  / 2p=m / L , L, m 是不可约的整数，则信号的周期为 L。 用 MATLAB 产生序列 MATLAB 中的基本函数： exp, sin, cos, square, sawtooth 例 用 MATLAB 产生指数序列 x[k]=Kaku[k] a = input('输入指数 a = '); K = input('输入常数 K = '); N = input ('输入序列长度 N = '); k = 0:N; x = K*a.^k; stem(k,x); xlabel('时间');ylabel('幅度'); title(['\alpha = ',num2str(a)]); cos((0 + 2n)k) = cos(0 k) nZ j t x t e  ( ) = j Tk j k t kT x k x t e e   [ ] = ( ) = = =

1.1.2序列的基本运算1)翻转(time reversal)x[K]->x[-k]2)位移(延迟)x[K]-→ x[k-M]3)抽取(decimation)x[K]→ x[MK]4)内插(interpolation)[x[k/M】k是M的整数倍x,[k]=其他105)卷积[k]-"- x[n]h[k-n]例：已知 x[K] * x2[K]=y[K],试求yi[K]=xi[k-n] *x2[k-m]。结论：yi[K]= y[k-(m+n)]例：x[]非零范围为Ni≤k≤N2，h[]的非零范围为N≤k< N4求：[K]=x[K]* h[K]的非零范围。结论：Ni+N≤k≤N4+N2例：用MATLAB函数conv计算两个序列的离散卷积。x=[-0.5,0,0.5,11; kx=-1:2:h=[1,1,1];kh=-2:0;y = conv(x, h);k=kx(1)+kh(1):kx(end)+kh(end),stem(k,y);xlabel(k');ylabel(y')

1.1.2 序列的基本运算 1)翻转(time reversal) x[k]→x[-k] 2)位移(延迟) x[k]→ x[k-N] 3)抽取(decimation) x[k]→ x[Mk] 4)内插(interpolation) 5)卷积 例：已知 x1[k] * x2[k]= y[k]，试求 y1[k]= x1[k-n] * x2[k-m]。 结论： y1[k]= y[k-(m+n)] 例：x[k] 非零范围为 N1 k  N2 ， h[k] 的非零范围为 N3 k N4 求： y[k]=x[k]* h[k]的非零范围。 结论：N1+ N3 k  N4+ N2 例：用 MATLAB 函数 conv 计算两个序列的离散卷积。 x=[-0.5,0,0.5,1]; kx=-1:2; h=[1,1,1];kh=-2:0; y = conv(x, h); k=kx(1)+kh(1):kx(end)+kh(end); stem(k,y); xlabel('k');ylabel('y');    = 其他 是 的整数倍 0 [ / ] [ ] x k M k M x k I y[k] x[n]h[k n] n = −  =−

1.2离散时间系统离散时x[K] →+[]间系统输出序列输入序列y[K] = T(x[K]1.2.1系统分类1.线性(Linearity)T(ax,[k]+bx,[k]) =aT(x[k]) +bT(x[k])例：设一系统的输入输出关系为y[K]=x?[K]试判断系统是否为线性？解：输入信号x[K]产生的输出信号T(x[K]}为T(x[k]]=x-[k]输入信号ax[K]产生的输出信号T(ax[K]}为T(ax [K]]= a?x[]除了a=0,1情况，T(ax[K]}+aT(x[K]]。故系统不满足线性系统的的定义，所以系统是非线性系统。2.时不变（Time-Invatiance)定义： 如 T(x[K]=y[K],则 T(x [k-n])=y[k-n]线性时不变系统简称为：LTI例：已知抽取器的输入和输出关系为y[k]=x[Mk]试判断系统是否为时不变的？解：输入信号x[K]产生的输出信号y[K]为y[K]-T( x[K]}= x[Mk]输入信号x[k-n]产生的输出信号T(x[k-n])为T(x[k-n]= x[Mk-n]由于x[Mk-n] *y[k-n]故系统是时变的

1.2 离散时间系统 y[k] = T{x[k]} 1.2.1 系统分类 1. 线性(Linearity) 例: 设一系统的输入输出关系为 y[k]=x 2 [k] 试判断系统是否为线性？ 解：输入信号 x [k]产生的输出信号 T{x [k]}为 T{x [k]}=x 2 [k] 输入信号 ax [k]产生的输出信号 T{ax [k]}为 T{ax [k]}= a 2x 2 [k] 除了 a=0,1 情况，T{ax [k]} aT{x [k]}。故系统不满足线性系 统的的定义，所以系统是非线性系统。 2.时不变(Time-Invatiance) 定义：如 T{x [k]}=y[k]，则 T{x [k-n]}=y[k-n] 线性时不变系统简称为：LTI 例: 已知抽取器的输入和输出关系为 y[k]=x[Mk] 试判断系统是否为时不变的？ 解：输入信号 x[k]产生的输出信号 y[k]为 y[k]=T{ x[k]}= x[Mk] 输入信号 x[k-n]产生的输出信号 T{x[k-n]}为 T{x[k-n]}= x[Mk-n] 由于 x[Mk-n] y[k-n] 故系统是时变的。 离散时 间系统 x[k] y[k] 输入序列 输出序列 { [ ] [ ]} { [ ]} { [ ]} 1 2 1 2 T ax k +bx k = aT x k +bT x k

x,[k]kRk012342345抽取器时变特性的图示说明3.因果性（Causality）定义：系统k时刻的输出只和k时刻及以前的输入有关。因果的 LTI：h[k]=0k[Kk]=M,+M,+1,-求和范围k-M,k+M,A当M2=0时，系统是因果的。(1(M,+M,+1) -M,≤k≤Mh[k]=其它0

抽取器时变特性的图示说明 3.因果性（Causality） 定义：系统 k 时刻的输出只和 k 时刻及以前 的输入有关。 因果的 LTI：h[k]=0, k<0. 例：M1+M2+1 点滑动平均系统定义为 当 M2=0 时，系统是因果的。 1 2 3 4 5 2 6 4 k 0 [ ] 1 x k -1 1 3 5 1 2 3 4 5 k -1 0 1 3 5 1 2 3 4 5 2 6 4 k -1 0 1 3 5 1 2 3 4 5 2 6 4 k -1 0 1 2 3 4 5 2 6 4 k -1 0 1 3 5 1 2 3 4 k -1 0 1 3 5 [ ] 1 1 [ ] 2 1 2 1 x k n M M y k M n M + + + = =− k k M1 k − M 2 k + 求和范围    + + −   = 0 其它 1/( 1) [ ] 1 2 2 M1 M M M k h k

4.稳定性定义(B.I.B.O）当输入，如输出满足，则称系统是稳定的。定理：LTI系统稳定的充分必要条件是Z[[k] = S<8k=-证：1.充分性[[]=[n[k-n]≤Z[n][k-n]≤M,Z[k-n]=M,Z[n]n2.必要性[h*[-k]/|[-k] [-k]+0x[k]=10h[-k]=0[0]=x[n]h[-n] =h*[-n][-n]/[-n] =-Z[n[-n]|= S例：（MI+M2+1点滑动平均）C[[k]=]1.2.2离散LTI系统的响应及性质1.单位脉冲响应（Impulseresponse）定义：h[k] = To[k]例：累加器：[k]=x[n]n=-h[k] = u[k]2.LTI系统对任意输入的响应T(x[k]) = T(x[n][k-n]]x[n]T(o[k-n]x[n][k-n]

4．稳定性 定义(B.I.B.O) 当输入, 如输出满足，则称系统是稳定的。 ●定理：LTI 系统稳定的充分必要条件是 证：1.充分性 2．必要性 例：(M1+M2+1 点滑动平均) 1.2.2 离散 LTI 系统的响应及性质 1. 单位脉冲响应（Impulse response） 定义: 例：累加器: 2. LTI 系统对任意输入的响应 h[k ] = u[k ]  =    k =− h[k] S =  − n y[k] x[n]h[k n] x[n] h[k n] n  − M h[k n] n  x − M h[n] n = x    − = − − −  = 0 [ ] 0 *[ ]/ [ ] [ ] 0 [ ] h k h k h k h k x k = − n y[0] x[n]h[ n] = − − − n h*[ n]h[ n]/ h[ n] h n S n =  [− ] =   =− = k h[k] 1 h[k] = T{[k]} y[k] x[n] k n =− = { [ ]} = { [ ] [ − ]} n T x k T x n  k n = [ ] { [ − ]} n x n T  k n = − n x[n]h[k n]

= x[k]*h[k]y[k]= x[k]* h[k]3.用MATLAB求解差分方程描述的离散LTI系统N a,k-- b,[k-n]当N个初始条件和输入已知，就可由下式迭代计算出系统的输出。MN[k]=-(a, /α)y[k-n]+Z ((b, /a)x[k-n]>n=ln=0MATLAB提供了一个filter函数计算由差分方程描述的系统的响应。y=filter(b,a, x )b.a分别表示差分方程的系数。x表示输入序列。y表示输出序列。输出序列的长度和输入序列是相同的。系统的初始条件为零。例：M点的滑动平均(movingaverage)系统定为一[K]=x[k-n]M2受噪声干扰的信号为x [k]=s[k]+d [K]原始信号s[k]-(2k)0.9k噪声d[k]% Signal Smoothing by Moving Average FilterR= 51;%generate (-0.5, 05)Uniformly distributed%random numbersd = rand(1,R)-0.5;k=0:R-1;s=2*k.*(0.9.^k);f=s+d,figure(1), plot(k,d,'r-,k,s,'b--,k,f,'g-),xlabel(Timeindexk'),legend(d[kl,'sk],'fk')M=5; b = ones(M,1)/M; a = 1;y = filter(b,a,f),figure(2); plot(k,s,'b-,k,y,'r-),xlabel(Time index k')legend('s[k],y[k]);

y[k] = x[k]h[k] 3.用 MATLAB 求解差分方程描述的离散 LTI 系统 当 N 个初始条件和输入已知，就可由下式迭代计算出系统的 输出。 MATLAB 提供了一个 filter 函数计算由差分方程描述的系统 的响应。 y=filter(b,a, x ) b,a 分别表示差分方程的系数。 x 表示输入序列。y 表示输出序列。 输出序列的长度和输入序列是相同的。系统 的初始条件为零。 例：M 点的滑动平均(moving average)系统定为 受噪声干扰的信号为 x [k]=s[k]+d [k] 原始信号 s[k]=(2k)0.9k 噪声 d[k] % Signal Smoothing by Moving Average Filter R = 51; %generate (-0.5, 05)Uniformly distributed %random numbers d = rand(1,R)-0.5; k=0:R-1; s=2*k.*(0.9.^k); f=s+d; figure(1); plot(k,d,'r-.',k,s,'b-',k,f,'g-'); xlabel('Time index k'); legend('d[k]','s[k]','f[k]'); M =5; b = ones(M,1)/M; a = 1; y = filter(b,a,f); figure(2); plot(k,s,'b-',k,y,'r-'); xlabel('Time index k'); legend('s[k]','y[k]'); = x[k]*h[k] [ ] [ ] 0 0 a y k n bn x k n M n n N n  − =  − = = [ ] ( / ) [ ] ( / ) [ ] 0 0 0 1 y k a a y k n bn a x k n M n n N n = − − + − = = [ ] 1 [ ] 1 0 x k n M y k M n =  − − =

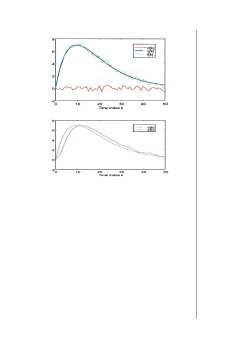
frkoO1020304050Time indexkP..1030405020Time index k

0 10 20 30 40 50 -2 0 2 4 6 8 Time index k d[k] s[k] f[k] 0 10 20 30 40 50 -2 0 2 4 6 8 Time index k s[k] y[k]

1.3离散时间信号的频域分析1.3.1离散Fourier级数(DFS)DFS的推导周期为N的单位脉冲序定义为3,[K]= S[k-rN]5,[K]x,[K]x4[k] = [k]+ 28,[k -2]一般地，一个周期为N周期序列可表示为N-1[K]=[]%[k-1]1=0-j2元N定义W~=e2wNk是N的整数倍+=N~[K]k不是N的整数倍周期为N的单位脉冲序列DFS表示1 N-1wo%[k] =Nm=o

1.3 离散时间信号的频域分析 1.3.1 离散 Fourier 级数(DFS) DFS 的推导 周期为 N 的单位脉冲序定义为 一般地，一个周期为 N 周期序列可表示为 0 N k 是 N 的整数倍 1 k 不是 N 的整数倍 周期为 N 的单位脉冲序列 DFS 表示  − = − = 1 0 1 [ ] ~ N m km N WN N  k [ ] ~ [ ] ~ [ ] ~ 1 0 x k x l k l N N l =  − − =  [ 2] ~ [ ] 2 ~ [ ] ~ x4 k =  4 k +  4 k − 2 k 0 1 2 3 4 1 [ ] ~ 4 x k 0 1 2 3 4 1 k 5 [ ] [ ] ~ k k rN r N =  −  =−   [ ] ~ 5  k N j N W e 2 − 定义 =  − =     = 1 0 N l kl WN [ ] ~ = N N k