《数字信号处理》课程教学资源（设计指导）第3章 系统分析与设计

第3章系统分析与设计信息系统就是为了有效的传输和交换信息而对载荷信息的信号进行加工、处理和变换的设备的总称。系统根据输入、输出信号的不同分为连续系统和离散系统。其分析方法有卷积法，零输入、零状态法，变换域法等。3.1连续系统分析3.1.1卷积积分法求解系统的响应对LTI连续系统，输入信号为x(y)，输出信号为y()，系统的冲激响应为h(t)则输入、输出之间的关系为：时域：y(t)=x()*h()频域：Y(j@)=X(j)H(jo)其中线性卷积的计算引入了DFT分析连续信号的频谱。例1：图（A）和（B）分别表示一个LTI连续系统的输入x(t)和单位冲激响应h(t)，试利用DFT的快速算法计算该系统的零状态响应。+th(t)x(t)(A)(B)134解：T=1/8; Tx=3 ; Mx=Tx/T;Th=4; Mh =Th/T;L=Mh+Mx-1;

第 3 章 系统分析与设计 信息系统就是为了有效的传输和交换信息而对载荷信息的信号进行加工、处理 和变换的设备的总称。系统根据输入、输出信号的不同分为连续系统和离散系统。 其分析方法有卷积法，零输入、零状态法，变换域法等。 3.1 连续系统分析 3．1．1 卷积积分法求解系统的响应 对 LTI 连续系统，输入信号为 x(t)，输出信号为 y(t)，系统的冲激响应为 h(t)， 则输入、输出之间的关系为： 时域：y(t)=x(t)*h(t) 频域：Y(jω)=X(jω) H(jω) 其中线性卷积的计算引入了 DFT 分析连续信号的频谱。 例 1：图（A）和（B）分别表示一个 LTI 连续系统的输入 x(t)和单位冲激响应 h(t) ，试利用 DFT 的快速算法计算该系统的零状态响应。 x(t) h(t) （A） （B） 1 1 3 4 解： T=1/8; Tx=3 ; Mx=Tx/T; Th=4; Mh =Th/T; L=Mh+Mx-1;

N=64;x=[ones(1,Mx),zeros(1,N -Mx)];h=[ones(1,Mh),zeros(1,N -Mh)];X=T.*fft(x,N);,H=T.*fft(h,N);Y=X.*H;y=1/T.*ift(Y,N);figure(1);t=[0:N-1]*T;subplot(3,1,1); plot(t,x);ylabel(x(t)); title(Time domain');subplot(3,1,2); plot(t,h);ylabel(h(t));subplot(3,1,3); plot(t(2:N), real(y(1:N-1);ylabel(y(t);xlabel(Time (s));figure(2),Fs= 1/T,w-[0:N-1]*Fs/N;subplot(3,1,1); plot(w-Fs/2,fftshift(abs(x),ylabel(X(w)");title("Frequency domain);subplot(3,1,2); plot(w-Fs/2,fftshift(abs(H); ylabel(°H (w)I);subplot(3,1,3); plot(w-Fs/2,fftshift(abs(Y),ylabel(Y(w))xlabel (Frequency (Hz);

N=64; x=[ones(1,Mx),zeros(1,N -Mx)]; h=[ones(1,Mh),zeros(1,N -Mh)]; X=T.*fft(x,N); H=T.*fft(h,N); Y=X.*H; y=1/T.*ifft(Y,N); figure(1); t=[0:N-1]*T; subplot(3,1,1); plot(t,x); ylabel('x(t)'); title('Time domain'); subplot(3,1,2); plot(t,h); ylabel('h(t)'); subplot(3,1,3); plot(t(2:N), real(y(1:N-1))); ylabel('y(t)'); xlabel('Time (s)'); figure(2); Fs= 1/T; w=[0:N-1]*Fs/N; subplot(3,1,1); plot(w-Fs/2,fftshift(abs(x))); ylabel('|X(w)|');title('Frequency domain'); subplot(3,1,2); plot(w-Fs/2,fftshift(abs(H))); ylabel('|H (w)|'); subplot(3,1,3); plot(w-Fs/2,fftshift(abs(Y)));ylabel('|Y(w)|'); xlabel ('Frequency (Hz)');

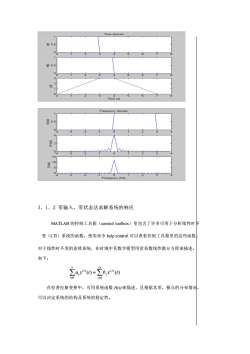
复0.50.620.5O2O1510LDreguency(Hz)3.1.2零输入、零状态法求解系统的响应MATLAB的控制工具箱（controltoolbox）里包含了许多可用于分析线性时拆变（LT）系统的函数，使用命令helpcontrol可以查看控制工具箱里的这些函数对于线性时不变的连续系统，在时域中其数学模型用常系数线性微分方程来描述。如下：Za,y(t)=)Zb,x((t)i=0j=0在拉普拉斯变换中，可用系统函数H(s)来描述，且根据其零，极点的分布情况可以决定系统的结构及系统的稳定性

3．1．2 零输入、零状态法求解系统的响应 MATLAB 的控制工具箱（control toolbox）里包含了许多可用于分析线性时不 变（LTI）系统的函数，使用命令 help control 可以查看控制工具箱里的这些函数。 对于线性时不变的连续系统，在时域中其数学模型用常系数线性微分方程来描述。 如下： ( ) ( ) ( ) 0 ( ) 0 a y t b x t j M j j i N i  i  = = = 在拉普拉斯变换中，可用系统函数 H(s)来描述，且根据其零，极点的分布情况， 可以决定系统的结构及系统的稳定性

2bsJ=oH(s) =as'i=0另外还可以用状态变量分析法进行系统描述。此设计完成用Matlab实现几种分析方法的相互转换。在Matlab中，描述系统的传递函数（系统函数）型tf(transferfunction),零极点型zp(zeropole)以及状态变量型ss(statespace)三种方式可以方便的转换Matlab相应的语句为：tf2zp—一系统函数型转换到零极点型tf2ss——系统函数型转换到状态变量型zp2tf——零极点型转换到系统函数型zp2ss——零极点型转换到状态变量型ss2tf—一状态变量型转换到系统函数型Ss2zp——一状态变量型转换到零极点型例2：已知描述LTI系统的数学模型为常系数线性微分方程：y"(t)+8 y"(t)+19 y'(t)+12y(t)=2 f'(t)+10f(t)将其转换为①零，极点型。②状态变量型。解：1 .num=[2,10];den-[1 8 19 12];[z,p,k]=tf2zp(num,den)2. num=[2,10]; den=[181912][a b c dj=tf2ss(num,den)MATLAB提供了用于分析LTI系统的函数，可对微分方程描述的系统的响应进行仿真。使用MATLAB命令可以计算系统的各种时间响应：如单位冲激响应、单位阶跃响应、零输入响应、零状态响应和完全响应。在调用这些函数时，需要用系数向量表示系统。在MATLAB中可使用向量b=[bm,bm-1,.,bi,bo]和向量a-[an,an-]..,al,ao]，分别

  = = = N i i i M j j j a s b s H s 0 0 ( ) 另外还可以用状态变量分析法进行系统描述。 此设计完成用Ｍatlab 实现几种分析方法的相互转换。 在 Matlab 中，描述系统的传递函数（系统函数）型 tf(transfer function),零极点 型 zp(zero pole)以及状态变量型 ss(state space)三种方式可以方便的转换。 Matlab 相应的语句为： tf2zp——系统函数型转换到零极点型 tf2ss——系统函数型转换到状态变量型 zp2tf——零极点型转换到系统函数型 zp2ss——零极点型转换到状态变量型 ss2tf——状态变量型转换到系统函数型 ss2zp——状态变量型转换到零极点型 例 2：已知描述 LTI 系统的数学模型为常系数线性微分方程： y (t) +8 y (t) +19 y (t) +12y(t)=2 f (t) +10 f ( t ) 将其转换为①零,极点型。②状态变量型。 解： 1 .num=[2,10];den=[1 8 19 12]; [z,p,k]=tf2zp(num,den) 2．num=[2,10]；den=[1 8 19 12] [a b c d]=tf2ss(num,den) MATLAB 提供了用于分析 LTI 系统的函数，可对微分方程描述的系统的响应 进行仿真。使用 MATLAB 命令可以计算系统的各种时间响应：如单位冲激响应、 单位阶跃响应、零输入响应、零状态响应和完全响应。 在调用这些函数时，需要用系数向量表示系统。 在 MATLAB 中可使用向量 b=[bm,bm-1,.,b1,b0]和向量 a=[an,an-1,.,a1,a0]，分别

为系统函数分子多项式和分母多项式的系数，注意均按s的降幂排列其系数直至s（1）用命令impulse可以求解系统的单位冲激响应：impulse(sys)：计算并画出系统的冲激响应，Sys可以是用命令tf、zpk或ss建立的系统函数。impulse(sys,t)：计算并画出系统在向量t定义的时间内的冲激响应。Y=impulse(sys,t)：向量Y保存对应时间的系统输出值。例3：已知系统的微分方程为y"(t)+5y(t)+6y(t)=2x(t)+8x(t)，计算该系统的单位冲激响应。解：b=[2,8];a=[1,5,6];t=0:0.1:10;y=impulse(b,a,t);（2）用命令step求解系统的单位阶跃响应step(sys)：计算并画出系统的冲激响应，sys可以是用命令tf、zpk或ss建立的系统函数。step(sys,t)：计算并画出系统在向量t定义的时间内的冲激响应。Y=step(sys,t)：向量Y保存对应时间的系统输出值。（3）：使用命令Isim求解系统在任意输入下的响应Isim(sys,x,t)计算并画出任意输入下系统的零状态响应，sys可以是用命令tf、zpk或ss建立的系统函数，t为时间向量定义时间范围，x为系统的输入。Isim(sys,x,t,zi）计算并画出系统的完全响应，但sys必须是状态空间形式的系统函数，zi为系统的初始状态。Y=lsim(sys,x,t,zi)：向量Y保存对应时间的系统输出值。b-[2,8];a-[1,5,6]sys=tf(b,a);

为系统函数分子多项式和分母多项式的系数，注意均按 s 的降幂排列其系数直至 s 0。 （1） 用命令 impulse 可以求解系统的单位冲激响应： impulse(sys)：计算并画出系统的冲激响应，sys 可以是用命令 tf、zpk 或 ss 建 立的系统函数。 impulse(sys, t)：计算并画出系统在向量 t 定义的时间内的冲激响应。 Y=impulse(sys, t)：向量 Y 保存对应时间的系统输出值。 例 3： 已知系统的微分方程为 y (t) + 5y (t) + 6y(t) = 2x (t) + 8x(t) ,计算该系统 的单位冲激响应。 解：b=[2,8];a=[1,5,6]; t=0:0.1:10; y=impulse(b,a,t); （2） 用命令 step 求解系统的单位阶跃响应 step (sys)：计算并画出系统的冲激响应，sys 可以是用命令 tf、zpk 或 ss 建立的系 统函数。 step (sys, t)：计算并画出系统在向量 t 定义的时间内的冲激响应。 Y=step (sys, t)：向量 Y 保存对应时间的系统输出值。 （3） 使用命令 lsim 求解系统在任意输入下的响应 lsim(sys, x, t)计算并画出任意输入下系统的零状态响应，sys 可以是用命令 tf、zpk 或 ss 建立的系统函数，t 为时间向量定义时间范围，x 为系统的输入。 lsim(sys, x, t, zi) 计算并画出系统的完全响应，但 sys 必须是状态空间形式的系统 函数，zi 为系统的初始状态。 Y=lsim(sys, x, t, zi)：向量 Y 保存对应时间的系统输出值。 b=[2,8];a=[1,5,6]; sys=tf(b,a);

t=0:10/300:10;x=exp(-t);y=lsim(sys,x,t);, plot(t,y);当系统具有初始状态时，使用Isim(sys,x,t,zi)命令格式，其中sys必须以状态方程形式求解，而且系统的初始条件必须转化为状态向量入在0时刻的初始值。例如求上述系统在初始条件为y(0)=-3,y(0)=0，输入x(t)=e-u(t)时的完全响应。使用下面命令可得到状态方程形式的系统函数。b-[2,8];a-[1,5,6];[A,B,C,D]=tf2ss(b,a);sys=ss(A,B,C,D)输出为各矩阵的值，依次为：ABCD计算零输入响应的程序如下：b-[2,8];a-[1,5,6][A,B,C,D]=tf2ss(b,a);sys=ss(A,B,C,D);t=0:10/300:10;x=zeros(1,length(t);zi-[-9/2,3/4];y=lsim(sys,x,t,zi);3.1.3系统函数的零、极点对系统的频响特性Hj9）的影响：连续因果LTI连续系统的系统函数H(s)的极点全部位于左半平面时，系统的频响特性H(jQ)可由H(s)求出。使用MATLAB命令freqs(b,a)可计算系统的频率特性H(jQ)。例4：已知某系统的系统函数为：1H(S)，求系统的幅频率曲线|H(jQ）I~Q。(S+1)(S? +S+1)

t=0:10/300:10; x=exp(-t); y=lsim(sys,x,t); plot(t,y); 当系统具有初始状态时，使用 lsim(sys, x, t, zi)命令格式，其中 sys 必须以状态 方程形式求解，而且系统的初始条件必须转化为状态向量λ在 0 时刻的初始值。 例如求上述系统在初始条件为 y(0- )=-3,y`(0- )=0，输入 x(t)=e –t u(t)时的完全响应。 使用下面命令可得到状态方程形式的系统函数。 b=[2,8];a=[1,5,6]; [A,B,C,D]=tf2ss(b,a); sys=ss(A,B,C,D) 输出为各矩阵的值，依次为：ABCD 计算零输入响应的程序如下： b=[2,8];a=[1,5,6]; [A,B,C,D]=tf2ss(b,a); sys=ss(A,B,C,D); t=0:10/300:10; x=zeros(1,length(t)); zi=[-9/2,3/4]; y=lsim(sys,x,t,zi); 3．1．3 系统函数的零、极点对系统的频响特性 H(jΩ)的影响： 连续因果 LTI 连续系统的系统函数 H(s)的极点全部位于左半平面时，系统的频 响特性 H (jΩ)可由 H(s)求出。 使用 MATLAB 命令 freqs(b,a)可计算系统的频率特性 H (jΩ)。 例 4：已知某系统的系统函数为： H(S) = ( 1)( 1) 1 2 S + S + S + ，求系统的幅频率曲线|H(jΩ) |~Ω

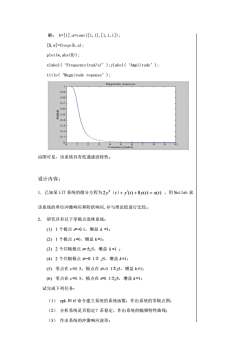
解：b=[1];a=conv([1,1],[1,1,1]);[H, w]=freqs (b, a) :plot (w,abs(H));xlabel(“Frequency(rad/s)):ylabel(“Amplitude");title(Magnitude reponse');Magnitude response0.90.80.70.60.30.20.10Freguency(rad由图可见，该系统具有低通滤波特性。设计内容：1.已知某LIT系统的微分方程为2y"（t)+y(t)+8y(t)=x(），用Matlab求该系统的单位冲激响应和阶跃响应，并与理论值进行比较。2.研究具有以下零极点连续系统：(1）1个极点s=-0.1，增益k=1;(2）1个极点s=0，增益k=l；(3）2个共轭极点s=土j5，增益k=1；(4）2个共轭极点s=-0.1±j5，增益k=1；(5）零点在s=0.5，极点在s=-0.1土j5，增益k=1：(6）零点在s=0.5，极点在s=0.1±j5，增益k=1；试完成下列任务：（1）zpk和tf命令建立系统的系统函数：作出系统的零极点图；（2）分析系统是否稳定？若稳定，作出系统的幅频特性曲线：（3）作出系统的冲激响应波形：

解： b=[1];a=conv([1,1],[1,1,1]); [H,w]=freqs(b,a); plot(w,abs(H)); xlabel(‘Frequency(rad/s)’);ylabel(‘Amplitude’); title(‘Magnitude reponse’); 由图可见，该系统具有低通滤波特性。 设计内容： 1．已知某 LIT 系统的微分方程为 2y （t）+ y (t) + 8y(t) = x(t) ，用 Matlab 求 该系统的单位冲激响应和阶跃响应,并与理论值进行比较。 2． 研究具有以下零极点连续系统： (1) 1 个极点 s=-0.1，增益 k =1； (2) 1 个极点 s =0，增益 k =1； (3) 2 个共轭极点 s=±j5，增益 k =1 ； (4) 2 个共轭极点 s=-0 .1± j5，增益 k =1； (5) 零点在 s =0. 5，极点在 s=-0 .1±j5，增益 k =1； (6) 零点在 s =0. 5，极点在 s=0 .1±j5，增益 k =1； 试完成下列任务： （1） zpk 和 tf 命令建立系统的系统函数；作出系统的零极点图； （2） 分析系统是否稳定？若稳定，作出系统的幅频特性曲线； （3） 作出系统的冲激响应波形；

（4）详细列出根据零极点分析系统特性的过程。3.已知系统函数为y(t)+10y(t)=2x(t),y(0-)=l，输入x()=u(t)，计算该系统的响应，并与理论分析结果做比较；详细列出系统响应分析的步骤。4S+11.已知一个连续系统的s域模型为：H(S)=求x(t)输入S3+3S?+2S分别为u(t)，sintu(t)，eu(t)时，求解系统的输出，并与理论分析结果做比较2.，寻找一个实际系统（如马达、受控过程等）的数学模型，利用MATLAB求解系统的响应；思考题：(1）系统函数零极点对系统频响的影响？(2）设计因果稳定、实系数的低通、高通、带通、带阻滤波器，如何布置零极点?(3）零极点对冲激响应波形有何影响？（4）因果稳定系统对系统函数零极点的要求是什么？（5）零极点知识在实际技术中的应用？（6）连续系统响应的计算机求解可以分为哪些方法？各是什么原理？3.2离散系统分析3.2.1卷积和法求解系统的响应对LTI离散系统，若输入序列为x(n)，输出序列为y(n)，系统的单位响应为h(n)，则输入、输出之间的关系为时域：y(n)=x(n)h(n)频域：Y(k)=X(k) H(k)利用循环卷积与线性卷积的关系，采用DFT计算系统的响应。其中线性卷积的计算引入了DFT分析离散序列的频谱

（4） 详细列出根据零极点分析系统特性的过程。 3． 已知系统函数为 y (t) +10y(t) = 2x(t) ,y(0-)=1，输入 x (t) = u(t)，计算该 系统的响应，并与理论分析结果做比较；详细列出系统响应分析的步骤。 1. 已知一个连续系统的 s 域模型为：H(S)= S S S S 3 2 4 1 3 2 + + + ,求 x(t)输入 分别为 u(t),sintu(t),e-t u(t)时，求解系统的输出，并与理论分析结果做比较. 2. .寻找一个实际系统（如马达、受控过程等）的数学模型，利用 MATLAB 求解 系统的响应； 思考题: (1) 系统函数零极点对系统频响的影响？ (2) 设计因果稳定、实系数的低通、高通、带通、带阻滤波器，如何布置零极 点？ (3) 零极点对冲激响应波形有何影响？ (4) 因果稳定系统对系统函数零极点的要求是什么？ (5) 零极点知识在实际技术中的应用？ (6) 连续系统响应的计算机求解可以分为哪些方法？各是什么原理？ 3.2 离散系统分析 3．2．1 卷积和法求解系统的响应 对 LTI 离散系统，若输入序列为 x(n)，输出序列为 y(n)，系统的单位响应为 h(n)，则输入、输出之间的关系为： 时域：y(n)=x(n)  h(n) 频域：Y(k) =X(k) H(k) 利用循环卷积与线性卷积的关系，采用 DFT 计算系统的响应。其中线性卷积 的计算引入了 DFT 分析离散序列的频谱

3.2.2零输入、零状态法求解系统的响应LTI离散系统可用系统函数H（z）的分子分母多项式形式、零极点-增益形式或状态空间形式来描述。（1）系统函数的分子分母多项式形式H(）：离散系统的差分方程为：NZa,(n-i)=Zb,x(n-i)ao =1i=0i=0对上式两边同取z变换，可得：B(a) =k (1-r=")(1-rz")..(1-rm=")H(2)= A(=)(1- p,z-")(1- P2--")...(1- pn=-")在MATLAB中可使用向量b=[bo,b..bm]和向量a=[1,ai,a2.ax]分别表示分子多项式和分母多项式的系数，注意从Z按Z的降幂排列其系数。离散系统响应的求解除可以使用MATLAB命令Isim求解外，还可以使用命令filter来求解系统响应。1+ 22-1例1：已知系统函数为H(z)=1+0.42--0.12-，求：(1）系统的脉冲响应h(n);(2）输入x(n)=u(n)，求系统的零状态响应y(n)：(3）输入x(n)=u(n)，初始条件y(-1)=1,y(-2)=2,求系统的完全响应y(n)解:(1)计算前11个时刻的h(n);N=11;b-[1,2];a-[1,0.4,-0.12];x=[1,zeros(1,N-1)];y=filter(b,a,x)Columns 1 through 51.00001.6000-0.52000.4000-0.2224Columns6through10

3．2．2 零输入、零状态法求解系统的响应 LTI 离散系统可用系统函数 H（z）的分子分母多项式形式、零极点-增益形式 或状态空间形式来描述。 （1） 系统函数的分子分母多项式形式 H (z) ： 离散系统的差分方程为： ( ) ( ) 0 0 a y n i b x n i M i i N i  i − =  − = = a0 = 1 对上式两边同取 z 变换，可得： (1 )(1 ) (1 ) (1 )(1 ) (1 ) ( ) ( ) ( ) 1 1 2 1 1 1 1 2 1 1 − − − − − − − − − − − − = = p z p z p z r z r z r z k A z B z H z n m   在 MATLAB 中可使用向量 b=[b0,b1,.,bM]和向量 a=[1,a1,a2,.,aN]分别表示 分子多项式和分母多项式的系数，注意从 z 按 z 的降幂排列其系数。 离散系统响应的求解 除可以使用 MATLAB 命令 lsim 求解外，还可以使用命令 filter 来求解系统响应。 例 1：已知系统函数为 H(z)= 1 2 1 1 0.4 0.12 1 2 − − − + − + z z z , 求 : (1) 系统的脉冲响应 h(n)； (2) 输入 x(n)=u(n)，求系统的零状态响应 y(n): (3) 输入 x(n)=u(n)，初始条件 y(-1)=1,y(-2)=2,求系统的完全响应 y(n) 解: (1)计算前 11 个时刻的 h(n); N=11; b=[1,2];a=[1,0.4,-0.12]; x=[1,zeros(1,N-1)]; y=filter(b,a,x) Columns 1 through 5 1.0000 1.6000 -0.5200 0.4000 -0.2224 Columns 6 through 10

0.1370-0.08150.0490-0.02940.0176Columns 11 through 15-0.01060.0023-0.00140.0063-0.0038Column 160.0008(2)计算前11个时刻的零状态响应N=11;b=[1,2];a=[1,0.4,-0.12];x=ones(1,N);y=filter(b,a,x)Columns 1 through 51.00002.60002.08002.48002.2576Columns6through102.39462.31312.36212.33272.3504Column 112.3398(3）计算前11个时刻的完全响应(n)b-[1,2];a-[1,0.4,-0.12];x=ones(1,N);zi=filtic(b,a,[1,2]);y=filter(b,a,x,zi);3.2.3离散系统函数的零极点对系统频域特性的影响因果LII离散系统的系统函数H(z)的极点全部位于平面单位园时，系统的频响特性可由H(z)求出，使用命令 freqz(b,a)可计算系统的频率特性。1+ 2~1例2：.已知某系统的系统函数为H(z)1-2+0.52-，求系统的幅频曲线=

0.1370 -0.0815 0.0490 -0.0294 0.0176 Columns 11 through 15 -0.0106 0.0063 -0.0038 0.0023 -0.0014 Column 16 0.0008 (2)计算前 11 个时刻的零状态响应 N=11; b=[1,2];a=[1,0.4,-0.12]; x=ones(1,N); y=filter(b,a,x) Columns 1 through 5 1.0000 2.6000 2.0800 2.4800 2.2576 Columns 6 through 10 2.3946 2.3131 2.3621 2.3327 2.3504 Column 11 2.3398 (3) 计算前 11 个时刻的完全响应 y(n) b=[1,2];a=[1,0.4,-0.12]; x=ones(1,N); zi=filtic(b,a,[1,2]); y=filter(b,a,x,zi); 3．2．3 离散系统函数的零极点对系统频域特性的影响 因果 LTI 离散系统的系统函数 H(z) 的极点全部位于 z 平面单位园时，系统的 频响特性可由 H(z)求出，使用命令 freqz(b,a)可计算系统的频率特性。 例 2:.已知某系统的系统函数为 H(z)= 1 2 1 1 0.5 1 − − − − + + z z z ，求系统的幅频曲线