《数字信号处理》课程教学资源（习题解答）ch2 离散傅立叶变换

2.6习题1332.6习题2-1已知序列x[k]=4S[k]+3[k-1]+28[k-2]+8[k-3]，试画出下列序列的波形。(1) x,[k]= x[(-k),]R,[k] ;(2) x,[k]= x[(k -2),]R,[k] ;(3) x,[k]= x[(3-k),]R,[K] 。解：x[K)=(4,3,2,1,0);x[(-k);]Rs[K] =(x[0], x[4], x[3], x[2], x[1])=(4, 0, 1, 2 ,3];x[(k-2),]R,[K]= (x[3], x[4], x[0], x[1], x[2])=(1, 0, 4, 3, 2];x[(3-k),]R,[]= (x[3], x[2], x[1],x[0], x[4])=(1, 2, 3, 4, 0]g[K]和h[K]是如下给定的有限序列2-2g[k]={5 24-1 2),h[k]=(-34 -1)(1)计算g[K]和h[k]的线性卷积[K]-g[K]+h[K];(2)计算g[k]和[K]的6点循环卷积yic[K]-g[K]?h[K];(3)计算g[k]和h[k]的7点循环卷积y2c[k]-g[k]③h[Kk];(4)计算g[K]和h[K]的8点循环卷积y3c[k]-g[k]③h[k]:(5）比较以上结果，有何结论？-991417-14-2)解： (1)yi[k]=(-15-99)1417-14(2) yic[k]-(-17-991417-14-2) (3) y2c[k]=(-15-9921417-1401(4) y3c[K)=(-15（5）序列的循环卷积与序列的线性卷积存在内在联系，在一定条件下，可以利用序列的循环卷积计算序列的线性卷积。2-3试证 N点序列x[k]的离散傅里叶变换X[m]满足Parseval恒等式[X[m]N-1 N-I[X[m] =-证明：Z X[m]X'[m]NON=O2x[mx[kjWmNL(k=0

2.6 习题 133 2.6 习 题 2-1 已知序列 x[k] = 4d[k] + 3d[k -1] + 2d[k - 2] + d[k - 3]，试画出下列序列的波形。 (1) [ ] [( ) ] [ ] 1 5 5 x k = x -k R k ； (2) [ ] [( 2) ] [ ] 2 5 5 x k = x k - R k ； (3) [ ] [(3 ) ] [ ] 3 5 5 x k = x - k R k 。 解： x[k]={4, 3, 2, 1,0}; x[(-k)5 ]R5 [k] ={x[0], x[4], x[3], x[2], x[1]}={4, 0, 1, 2 ,3}; x[(k-2)5 ]R5 [k] = {x[3], x[4], x[0], x[1], x[2]}={1, 0, 4, 3, 2}; x[(3-k)5 ]R5 [k] = {x[3], x[2], x[1], x[0], x[4]}={1, 2, 3, 4, 0} 2-2 g[k]和 h[k]是如下给定的有限序列 g[k]={5 2 4 -1 2}， h[k]={-3 4 -1 } (1) 计算 g[k]和 h[k]的线性卷积 yL [k]=g[k]*h[k]； (2) 计算 g[k]和 h[k]的 6 点循环卷积 y1C[k]=g[k]Ä h[k]； (3) 计算 g[k]和 h[k]的 7 点循环卷积 y2C[k]=g[k]Ä h[k]； (4) 计算 g[k]和 h[k]的 8 点循环卷积 y3C[k]=g[k]Ä h[k]； (5) 比较以上结果，有何结论？ 解：(1) yL [k]={ -15 14 -9 17 -14 9 -2} (2) y1C[k]={-17 14 -9 17 -14 9} (3) y2C[k]={-15 14 -9 17 -14 9 -2} (4) y3C[k]={-15 14 -9 17 -14 9 -2 0} (5) 序列的循环卷积与序列的线性卷积存在内在联系，在一定条件下，可以利用序列的 循环卷积计算序列的线性卷积。 2-3 试证 N 点序列 x[k]的离散傅里叶变换 X[m]满足 Parseval 恒等式 2 1 0 1 0 2 [ ] 1 [ ] X m N x k N m N k å å - = - = = 证明: [ ] [ ] 1 [ ] 1 1 0 2 1 0 X m X m N X m N N m N m * - = - = å = å * - = - = ÷ ÷ ø ö ç ç è æ = å å mk N N k N m X m x k W N [ ] [ ] 1 1 0 1 0

134第3章离散傅里叶变换快速算法NSI1Zx[]-X[mJW-mkNmOk=0N-1N-Z x [k]x[k]=Z x[k]k=0k=02-4Xm]表示2M点序列x[K]的DFT，当x[k]=-x[k+M，试证X|2r=0，=0,1,M-1。证明：现将x[K]按k的自然顺序分成前后两部分，即M-I2 M12M-1x[kjW=X[m]= DFT(x[k]} =x[kjW2m+x[kJWm>>=0=0k=MW(x[k]+Wm* x[k+ M) Wmk:由于WmM=e-mp=(-1)"，上式可写成WX[m]=(x[k]+(-1)"x[k +M])Wm当m为偶数时，（-1)"=1：当m为奇数时，（-1)"=-1。因此，根据m为偶数或奇数将频域序列Xml分成偶数组和奇数组。用X[2rl表示偶数组，X[2r+11表示奇数组，则有X[2m-2(x[K]+x[k+M])W2,r=0,1,.,M-1K=0M-17X[2r+1]=(x[k]--[k+M)wawWm, r= 0,].., M-1k=0由于x[k]=-x[k+M]，故有X[2r]=0，=0,1,*,M-1，证毕。2-5g[K]和h[K]是6点的有限序列，G[m]和Hm]分别表示它们的DFT(1)如果G[m)=(1+i，-2.1+j3.2，-1.2-j2.4，0,0.9+j3.1，-0.3+i1.17，若存在h[K]=g[(k-4),]R.[K],试由 G[m]确定 H[m]。(2)如果g[k]=(4.1，3.5,1.2,5,，2，3.3)，且存在H[m]=G[(m-3)]Rs[m],试由g[K]确定h[K]。解：由DFT的时域循环位移性质可得(1) H[m]=DFT(g[(k-4)。JR.[k]) =W4"G[m]=(1+j,-1.7213- 3.4187j,-1.4785 + 2.2392j, 0,-3.1347- 0.7706j,1.1026 -0.2902j)(2）由DFT的频域循环位移性质可得h[k]=g[kjW-3k =(-1)*g[k] = (4.1, -3.5, 1.2, -5, 2, -3.3]2-6设x[k]是一10点的有限序列[k)=(2110320346)不计算DFT，试确定下列表达式的值，并用MATLAB，通过计算DFT验证

134 第 3 章 离散傅里叶变换快速算法 mk N N m N k X m W N x k - - = * - = = å å [ ] 1 [ ] 1 0 1 0 2 1 0 1 0 x [k]x[k] x[k] N k N k å å - = * - = = = 2-4 X[m]表示 2M 点序列 x[k]的 DFT，当 x[k]= -x[k+M]，试证 X[2r]=0，r=0,1,. ,M-1。 证明： 现将 x[k]按 k 的自然顺序分成前后两部分，即 2 1 2 0 [ ] DFT{ [ ]} [ ] M km M k X m x k xkW - = = = å 1 2 1 2 2 0 [ ] [ ] M M mk mk M M k k M x k W xkW - - = = = + å å ( ) 1 2 2 0 [ ] [ ] M mM mk M M k x k W x kMW - = = å + + 由于 j p 2 ( 1) mM m m W e M - = = - ，上式可写成 ( ) 1 2 0 [ ] [ ] ( 1) [ ] M m mk M k X m x k x kMW - = = å + - + 当 m 为偶数时，(-1) = 1 m ；当 m 为奇数时，(-1) = -1 m 。因此，根据 m 为偶数或奇数将频 域序列 X[m]分成偶数组和奇数组。用 X[2r]表示偶数组，X[2r+1] 表示奇数组，则有 ( ) 1 2 2 0 [2 ] [ ] [ ] , 0,1, , 1 M rk M k X r x k x k M WrM - = = å + + = - L ( ) 1 2 2 2 0 [2 1] [ ] [ ] , 0,1 , 1 M k rk M M k X r x k x k M W W r M - = + = å - + ×=- L 由于 x[k]= -x[k+M]，故有 X[2r]=0，r=0,1, . , M-1，证毕。 2-5 g[k]和 h[k]是 6 点的有限序列，G[m]和 H[m]分别表示它们的 DFT (1) 如果 G[m]={1+j, -2.1+j3.2, -1.2-j2.4, 0, 0.9+j3.1, -0.3+j1.1}, 若存在 h[k]=g[(k-4)6 ]R6 [k], 试由 G[m]确定 H[m]。 (2) 如果 g[k]={4.1, 3.5, 1.2, 5, 2, 3.3}, 且存在 H[m]=G[(m-3)6 ]R6 [m], 试由 g[k]确定 h[k]。 解：由 DFT 的时域循环位移性质可得 (1) 4 6 6 6 [ ] DFT{ [( 4) ] [ ]} [ ] m H m =-= g k R k W G m ={1+j, -1.7213- 3.4187j, -1.4785 + 2.2392j, 0, -3.1347 - 0.7706j, 1.1026 - 0.2902j} (2) 由 DFT 的频域循环位移性质可得 = = - = - [ ] [ ] ( 1) [ ] 3 6 h k g k W g k k k {4.1, -3.5, 1.2, -5, 2, -3.3} 2-6 设 x[k]是一 10 点的有限序列 x[k]={2 1 1 0 3 2 0 3 4 6} 不计算 DFT，试确定下列表达式的值，并用 MATLAB, 通过计算 DFT 验证

2.6习题135ae-(4m/1) [m) (5) ≥ [X[m]7(3)X[m) (4)(1) x[0], (2) X[5] M=0m=0-解： (1) 101=Zx[k]=22k=099x[kjw*=7(2) X[5] =Z :(-1)* x[k]= -2k=0k=0W(3)X[m]= 10x[0|=20m=0(4) e-i(4pm/5) X[m] = W,tm X[m] → x[(k - 4)o]R.[K]We-i(4pm/5) X[m]= 10 x[6]=09>[[m]=10 []”=800(5)mz0k=02-7Xm]表示12点实序列x[K]的DFT。Xm]前7个点的值为XT0=10,XT1]=-5-j4,XI2]=3-j2.X[3]=1+j3X[4]=2+j5, X[5]=6-j2,X[6]=12不计算IDFT，试确定下列表达式的值，并用MATLAB验证你的结论。艺(4)11eK2p/3)x[K] (5) [k](1)x[0], (2)x[6](3)22K=01-0解：X=[10, -5-j4, 3-j2,6-j2,12,6+2j,2-5j1+j3,2+j5,1-3j.3+2i-5+4i].111TX[m]=3(1)x[0] =1220A=W11 X[mJWam(2) x[6] =(-1)"X|m|=7/3N120120=W(3)x[K] = X[0] = 10k=0e(2p:/3) x[k] =Z w*x[k](4)= X *[4]=2- j5k=0k=011[X[m=85/2x[k] = N(5)12=0(2k)x[K]的N点DFT。2-8已知x[k]的N点DFT为Xm]，试求y[k]=cos(N

2.6 习题 135 (1) X[0], (2) X[5] (3) [ ] 9 0 X m m å= (4) [ ] (4 / 5) 9 0 e X m j m m - p = å (5) 2 9 0 X[m] m å= 解：(1) [0] [ ] 9 0 X x k k å= = =22 (2) k k X x k W 5 10 9 0 [5] å [ ] = = ( 1) [ ] 9 0 x k k k = å - = = -2 (3) [ ] 10 [0] 9 0 X m x m å = = =20 (4) j(4p / 5) e [ ] m X m - = [ ] 4 W10 X m m ® [( 4) ] [ ] 10 10 x k - R k 9 j(4p / 5) 0 [ ] 10 [6] 0 m m e X m x - = å = × = (5) 2 9 0 X[m] m å= 2 9 0 10 x[k] k å= = =800 2-7 X[m]表示 12 点实序列 x[k]的 DFT。X[m]前 7 个点的值为 X[0]=10, X[1]=-5-j4, X[2]=3-j2, X[3]=1+j3 X[4]=2+j5, X[5]=6-j2, X[6]=12 不计算 IDFT，试确定下列表达式的值，并用 MATLAB 验证你的结论。 (1) x[0], (2) x[6] (3) [ ] 11 0 x k k å= (4) 11 j(2p / 3) 0 [ ] k k e x k = å (5) 2 11 0 x[k] k å= 解： X=[10, -5-j4, 3-j2, 1+j3, 2+j5, 6-j2, 12, 6+2j, 2-5j 1-3j, 3+2j -5+4j] (1) [ ] 12 1 [0] 11 0 x X m k å= = =3 (2) m k x X m W 6 12 11 0 [ ] 12 1 [6] å= = ( 1) [ ] 12 1 11 0 X m m k = å - = = 7/3 (3) [ ] [0] 10 11 0 å = = = x k X k (4) 11 11 j(2p / 3) 4 12 0 0 e [ ] [ ] *[4] k k k k x k W x k X * = = æ ö = = = ç ÷ è ø å å 2- j5 (5) [ ] 85/ 2 12 1 [ ] 2 11 0 2 11 0 å = å = = = x k X m k m 2-8 已知 x[k]的 N 点 DFT 为 X[m]，试求 ) [ ] 2p [ ] cos( lk x k N y k = 的 N 点 DFT

136第3章离散傅里叶变换快速算法Pk12P12P 1k)x[k] =解：y[k]=cos(-x[klex+=x[k]eN2n根据DFT的频域循环位移特性，可得y[K]的N点DFT为Y[m)= DFT([K]),=→x[(m-1) ]+X[(m+1)]2n2-9已知一9点实序列的DFT在偶数点的值为X[0]=3.1，X[2]=2.5+j4.6,X[4]=-1.7+j5.2,X[6]=9.3+j6.3,X[8]=5.5-j8.0。确定DFT在奇数点的值。解：根据实序列DFT的对称特性Xm=X[N-m]，可得X[1]=X*[9-1]=X*[8]=5.5+j8.0,X[3]=X*[9-3]=X*[6]=9.3-j6.3X[5]=X*[9-5]=X*[4]=-1.7-j5.2;X[7]=X*[9-7]=X*[2]=2.5-j4.62-10已知一9点实序列在5个点上的DFT值为X[0]=23，X[1]=2.2426-j，X[4]=-6.374+j4.1212,X[6]=6.5+j2.589,XI7)=-4.1527-j0.2645，试确定其他4个点的DFT值。解：根据实序列DFT的对称特性X[m]=X[N-m]，可得X[2]=X*[9-2]=X*[7]=-4.1527+j0.2645;X[3]=X*[9-3]=X*[6]=6.5-j2.589;X[5]=X*[9-5]=X*[4]=-6.374-j4.1212;X[8]=X*[9-8]=X*[1]=2.2426+j2-11 已知一7 点序列为 x[0]=5,x[1]=3,x[2]=-2,x[3]=-4,x[4]=1,x[5]=2,x[6]-0 。Y[m]=W4mX[m]。不计算IDFT,，试确定序列>[K]。解：由DFT时域循环位移动特性有[k]=x[(k-4),]R,[K]={-4, 1, 2, 0, 5, 3, -2)2-12x[K]=(1-12300)]，X[m]是其DFT。G[m]=W3mX[m]，不计算IDFT，试确定6点序列g[K]。解：由DFT时域循环位移动特性有g[k]=x[(k-3),]R[k]=(0, 0, 3, 1, -1, 2]2-13已知x[K是一N点的有限序列，试求()[K)}-DFT(DFT(x[K]))(2)g[K)=DFT(DFT(DFT(DFT(x[K])))解：(1)[K)-DFT(DFT(x[K]))=DFT(X[m])

136 第 3 章 离散傅里叶变换快速算法 解： lk N lk N lk x k x k e x k e N y k 2p -j 2p j [ ] 2 1 [ ] 2 1 ) [ ] 2p [ ] = cos( = + 根据 DFT 的频域循环位移特性，可得 y[k]的 N 点 DFT 为 [( ) ] 2 1 [( ) ] 2 1 [ ] DFT{ [ ]} N N Y m = y k = X m - l + X m + l 2-9 已知一 9 点实序列的 DFT 在偶数点的值为 X[0]=3.1, X[2]=2.5+j4.6, X[4]=-1.7+j5.2, X[6]=9.3+j6.3, X[8]=5.5-j8.0。确定 DFT 在奇数点的值。 解：根据实序列 DFT 的对称特性 X[m]=X * [N-m]，可得 X[1]=X*[9-1]= X*[8]= 5.5+j8.0; X[3]=X*[9-3]= X*[6]= 9.3-j6.3 X[5]=X*[9-5]= X*[4]= -1.7-j5.2; X[7]=X*[9-7]= X*[2]= 2.5-j4.6; 2-10 已知一 9 点实序列在 5 个点上的 DFT 值为 X[0]=23, X[1]=2.2426-j, X[4]= -6.374+j4.1212, X[6]=6.5+j2.589, X[7]= -4.1527-j0.2645，试确定其他 4 个点的 DFT 值。 解：根据实序列 DFT 的对称特性 X[m]=X * [N-m]，可得 X[2]=X*[9-2]= X*[7]= -4.1527+j0.2645; X[3]=X*[9-3]= X*[6]= 6.5-j2.589； X[5]=X*[9-5]= X*[4]= -6.374-j4.1212; X[8]=X*[9-8]= X*[1]= 2.2426+j 2-11 已知一 7 点序列为 x[0]=5, x[1]=3, x[2]= -2, x[3]=-4, x[4]=1, x[5]=2, x[6]=0 。 [ ] [ ] 4 Y m W7 X m m = 。不计算 IDFT，试确定序列 y[k]。 解：由 DFT 时域循环位移动特性有 [ ] [( 4) ] [ ] 7 7 y k = x k - R k ={-4，1，2，0，5，3，-2} 2-12 x[k]={1 -1 2 3 0 0}，X[m]是其 DFT。 3 6 [ ] [ ] m G m = W X m ，不计算 IDFT，试确定 6 点序 列 g[k]。 解：由 DFT 时域循环位移动特性有 6 6 g[k] = - x[(k 3) ]R k[ ] ={0，0，3，1，-1，2} 2-13 已知 x[k]是一 N 点的有限序列，试求 (1) y[k]=DFT{DFT{x[k]}} (2) g[k]=DFT{DFT{DFT{DFT{x[k]}}}} 解：(1) y[k]=DFT{DFT{x[k]}} =DFT{ X[m]}

2.6习题13720X[m]em=0由于当x[K]的DFT为X[m]时，则x[N-k]的DFT为X[m]，即存在2Pmk1x[N-k]=XmleNm=0两边取共轭后可得20mk1 !x[N-k]=X[m]e7公m=0故[K]-Nx[N-K](2)g[K)-DFT(DFT(DFT(DFT(x[K))3)=DFT(DFT(N x[N-K))=N2 x[K]2-14x[K]和h[K]是在0≤k≤29范围内有定义的30点序列，并且h[k]=0,0≤k≤920 ≤k≤29.x[K] 和 h[K]的30 点循环卷积记为g[k],线性卷积记为y[K]。试确定在哪些点上有[K]=g[K]。解：h[n]1n0101929h[(-n)3o |= h[30 - n]n1120029h[(19- n)30] = h[19-n]L-n0929由图可知y[30]=g[0],y[31]=g[1],.....y[39]=g[9]y[19]=g[19],y[20]=g[20],....,y[29]=g[29]2-15（1）若N点序列x[kl,0≤k≤N-1，其N点DFT为Xm]。现构造一LxN点序列[x[k/ L], k = 0,L,.--(N -1)L[k] =其它0L是一正整数，试用Xm]表示y[K的LxN点DFT

2.6 习题 137 1 2p j 0 [ ] N mk N m Xme - - = = å 由于当 x[k]的 DFT 为 X[m]时，则 x * [N-k] 的 DFT 为 X * [m]，即存在 1 2p j * * 0 1 [ ] [ ] N mk N m x N k X m e N - = - = å 两边取共轭后可得 1 2p -j 0 1 [ ] [ ] N mk N m x N k X m e N - = - = å 故 y[k]=N x[N-k] (2) g[k]=DFT{DFT{DFT{DFT{x[k]}}}} = DFT{DFT{N x[N-k]}} =N 2 x[k] 2-14 x[k]和 h[k]是在 0 £ k £ 29 范围内有定义的 30 点序列，并且 h[k]=0, 0 £ k £ 9 , 20 £ k £ 29 . x[k] 和 h[k]的 30 点循环卷积记为 g[k], 线性卷积记为 y[k]。试确定在哪些点上 有 y[k]=g[k]。 解： 0 10 19 29 n h[n] 0 11 20 29 n [( ) ] [30 ] 30 h -n = h - n 0 9 29 n [(19 ) ] [19 ] 30 h - n = h - n 由图可知： y[30]=g[0], y[31]=g[1], . . y[39]=g[9] y[19]=g[19], y[20]=g[20], ,. . ,y[29]=g[29] 2-15 (1) 若 N 点序列 x[k], 0 £ k £ N -1，其 N 点 DFT 为 X[m]。现构造一 L´N 点序列 î í ì = - = 0, 其它 [ / ], 0, , ( 1) , [ ] x k L k L N L y k L L 是一正整数，试用 X[m]表示 y[k]的 L´N 点 DFT

138第3章离散傅里叶变换快速算法(2)一个7点序列x[K]的DFT为X[m)=(1,1,1,1,2,3,4)，试利用上述构造方法，求出21点序列y[k]的DFT。解：(1)序列y[K]实际上就是序列x[K]的L倍内插，由序列内插的定义，可得L倍内插序列y[K]的z 变换 Y(z)为Y(2)= [k}-= x[k/L)-* = Z x[n]-- =X(=")i)k=-素是工的整数倍所以L倍内插序列y[k]的频谱Y(ei)为i)Y(ej)=X(ejL2)将序列x[k]的频谱X(ei?)压缩L倍即可得L倍内插序列y[k]的频谱Y(ej)。由于序列的DFT是其频谱在[0，2元]上的等间隔抽样，故Y[m]是X[m]的L次的重复，即Y[m]-X[m]m=0,1....N-1Y[m+N]=X[m]m=0,1....N-1Y[m+(L-1)N]=X[m]m=0,1....N-1(2）由7点序列x[K]构造出21点序列y[k]时，L=3，故有Y[m)=(1, 1, 1, 1, 2, 3, 4, 1, 1, 1, 1, 2, 3, 4, 1, 1, 1, 1, 2, 3, 4)2-16Xm]是N点序列x[K]的DFT，N为偶数。两个N/2点序列定义为Nx,[Kk]= -_(x[2k]+x[2k+1],x,[k]=--(x[2k]-x[2k+1D),0≤k<222X,[m]和X[m]分别表示序列xi[K]和x2[]的 N/2点 DFT，试由X,[m]和X[m]确定x[K]的N点DFT。YN/2-1[WwI!?解：[2kJWWhDFT(x[2k]) =-k=01=0/=偶数(1+WN/3)Nx[1](X[m|+X[m+N /2D)22I=01=偶数N/2-1N-1[W1-12EZDFT(x[2k +1]) =7x[2k+1]Ww/2 =k=0(1-WIN/2N-WN(X[m]-X[m+N/2DW-"21=0二奇数所以X[m]={(1+W\")X[m)+{(1-W\")X[m+N /2](0≤m≤N/2-1

138 第 3 章 离散傅里叶变换快速算法 (2) 一个 7 点序列 x[k]的 DFT 为 X[m]={1, 1, 1, 1, 2, 3, 4}, 试利用上述构造方法， 求出 21 点序列 y[k]的 DFT。 解：(1) 序列 y[k]实际上就是序列 x[k]的 L 倍内插，由序列内插的定义，可得 L 倍内插序列 y[k] 的 z 变换 Y(z)为 k k Y z y k z - ¥ =-¥ ( ) = å [ ] k k L k x k L z - ¥ =-¥ = å [ / ] 是 的整数倍 nL n x n z - ¥ =-¥ = å [ ] ( ) L = X z i) 所以 L 倍内插序列 y[k]的频谱 Y(ejW )为 Y(ejW )= X(ejLW ) ii) 将序列 x[k]的频谱 X(ejW )压缩 L 倍即可得 L 倍内插序列 y[k]的频谱 Y(ejW )。 由于序列的 DFT 是其频谱在[0，2p]上的等间隔抽样，故 Y[m]是 X[m]的 L 次的重复， 即 Y[m]= X[m] m=0,1,. ,N-1 Y[m+N]= X[m] m=0,1,. ,N-1 . . Y[m+(L-1)N]= X[m] m=0,1,. ,N-1 (2) 由 7 点序列 x[k] 构造出 21 点序列 y[k]时，L=3，故有 Y[m]={1, 1, 1, 1, 2, 3, 4, 1, 1, 1, 1, 2, 3, 4, 1, 1, 1, 1, 2, 3, 4} 2-16 X[m]是 N 点序列 x[k]的 DFT，N 为偶数。两个 N/2 点序列定义为 1. 2 ( [2 ] [2 1]), 0 2 1 ( [2 ] [2 1]), [ ] 2 1 [ ] 1 = + + 2 = - + £ £ - N x k x k x k x k x k x k k X1 [m]和 X2 [m]分别表示序列 x1 [k]和 x2 [k]的 N/2 点 DFT，试由 X1 [m]和 X2 [m]确定 x[k]的 N 点 DFT。 解： mk N N k x k x k W / 2 / 2 1 0 DFT{ [2 ]} å [2 ] - = = / 2 / 2 1 0 [ ] ml N N l l å x l W - = = = 偶数 ml N lN N N l l W W x l 2 (1 ) [ ] 1 / 2 0 + = å - = = 偶数 ( [ ] [ / 2]) 2 1 = X m + X m + N mk N N k x k x k W / 2 / 2 1 0 DFT{ [2 +1]} = å [2 +1] - = ( 1)/ 2 / 2 1 1 [ ] - - = = = å m l N N l l x l W 奇数 m N ml N lN N N l l W W W x l - - = = - = å 2 (1 ) [ ] 1 / 2 0 奇数 m X m X m N WN - = ( [ ] - [ + / 2]) 2 1 所以 (1 ) [ / 2] 4 1 (1 ) [ ] 4 1 [ ] X1 m W X m W X m N m N m = + N + - + - - 0 £ m £ N / 2 -1

2.6习题139X,[m] ==(1-W")X[m]+=(1+W")X[m+N /2]0≤m≤N/2-14解上述方程即可得：0≤m≤N/2-1X[m]=(1+W")X,[m]+(1-W")X,[m]0≤m≤N/2-1X[m+N /2]=(1-W")X,[m]+(1+Wm)X,[m]2-17已知有限长N序列x[K]的z变换为X(=)，若对X(z)在单位圆上等间隔采样M点，且比M<N，试分析此M个样点序列对应的IDFTx[K]与序列x[K]的关系。解：如果m=0, 1,.., M-1X,[m]= X(=) 即X,[m]是X(=)在单位圆上M点等间隔抽样，根据频域抽样定理，则存在x[K]= IDFT(X[m])= 2福x[k +IM]· RM[K]I=0上式表明，将序列x[K]以M为周期进行周期延拓，取其主值区间[0，M-1]上的值即得序列x[K]。由于MKN，故在对x[K]以M为周期进行周期延拓时，必然存在重叠。2-18已知序列x[K]=3k+2,0≤k≤9,h[K]=(1,3,2),试按L=7对序列x[k]分段，并分别利用重叠相加法与重叠保留法计算线性卷积y[k]=x[k]*h[k]。解：（1）重叠相加法序列x[k]的长度N=10，若按L=7对序列进行分段，可以分解为以下2段：xo[k)=(2, 5, 8, 11, 14, 17, 20)xi[K]={23, 26, 29]将x[k]的各段xo[K]、x;[K]分别与序列h[k]线性卷积，可得各段卷积结果为yo[K)=(2, 11, 27, 45, 63, 81,99, 94, 40)yi[k]=(23,95,153, 139, 58)由于序列h[k]的长度M=3，通过相邻段M-1=2项的重叠相加，即可得到卷积序列y[k]=x[K]*h[k]为y[k]=( 2, 11, 27, 45, 63, 81, 99, 117, 135, 153, 139, 58)(2）重叠保留法由于序列h[k1的长度M-3，故每段与前一段应重叠M-1=2个样本。对于第一段需要在其前面添加2个零。因为L=7，且序列x[k]的长度N=10，则序列x[k]可划分为3段xo[k]=(0, 0, 2, 5, 8, 11, 14)x,[K)=(11, 14, 17, 20, 23, 26, 29,)x[K]{26,29,0,0,0,0, 0 )计算每段与h[k]的L=7点的循环卷积，得

2.6 习题 139 (1 ) [ / 2] 4 1 (1 ) [ ] 4 1 [ ] X2 m W X m W X m N m N m = - N + + + - - 0 £ m £ N / 2 -1 解上述方程即可得： [ ] (1 ) [ ] (1 ) [ ] X m W X1 m W X2 m m N m = + N + - 0 £ m £ N / 2 -1 [ / 2] (1 ) [ ] (1 ) [ ] X m N W X1 m W X2 m m N m + = - N + + 0 £ m £ N / 2 -1 2-17 已知有限长 N 序列 x[k] 的 z 变换为 X(z)，若对 X(z)在单位圆上等间隔采样 M 点，且比 M<N，试分析此 M 个样点序列对应的 IDFT x1 [k]与序列 x[k]的关系。 解：如果 2 p j 1 e [ ] ( ) m X m = X z z= M m=0, 1, . , M-1 即 X1 [m]是 X(z)在单位圆上 M 点等间隔抽样，根据频域抽样定理，则存在 1 1 [ ] IDFT{ [ ]} [ ] [ ] M l x k X m x k lMRk +¥ =-¥ = = å + × 上式表明，将序列 x[k]以 M 为周期进行周期延拓，取其主值区间[0，M-1]上的值即得序列 x1 [k]。 由于 M<N，故在对 x[k]以 M 为周期进行周期延拓时，必然存在重叠。 2-18 已知序列 x[k] = 3k + 2, 0 £ k £ 9, h[k] ={1,3,2},试按 L=7 对序列 x[k]分段，并分别利用 重叠相加法与重叠保留法计算线性卷积 y[k] = x[k]*h[k]。 解：(1) 重叠相加法 序列 x[k]的长度 N=10，若按 L=7 对序列进行分段，可以分解为以下 2 段： x0 [k]={2, 5, 8, 11, 14, 17, 20} x1 [k]={23, 26, 29} 将 x[k]的各段 x0 [k]、x1 [k]分别与序列h[k]线性卷积，可得各段卷积结果为 y0 [k]={2, 11, 27, 45, 63, 81, 99, 94, 40} y1 [k]={23, 95, 153, 139, 58} 由于序列 h[k] 的长度 M=3，通过相邻段 M-1=2 项的重叠相加，即可得到卷积序列 y[k] = x[k]*h[k]为 y[k]={ 2, 11, 27, 45, 63, 81, 99, 117, 135, 153, 139, 58} (2) 重叠保留法 由于序列h[k]的长度 M=3，故每段与前一段应重叠 M-1=2 个样本。对于第一段需要 在其前面添加 2 个零。因为 L=7，且序列 x[k]的长度 N=10，则序列 x[k]可划分为 3 段 x0 [k]={0, 0, 2, 5, 8, 11, 14} x1 [k]={11, 14, 17, 20, 23, 26, 29,} x2 [k]={26, 29, 0, 0, 0, 0, 0 } 计算每段与h[k]的 L=7 点的循环卷积，得

140第3章离散傅里叶变换快速算法y[k]= x[k]@ h[k]= (64, 28, 2, 11, 27, 45, 63]y,[k]= x,[k]@ h[k]= (+50, 105,81, 99, 117, 135, 153]y2[k]= x,[k]@h[k]= (26, 107,-139, 58, 0, 0, 0]去掉每个y,[k]前面的2个样本后，把各y[k]依次拼接在一起，即可得到输出序列为y[k]=(2, 11,27, 45, 63, 81, 99, 117, 135, 153, 139, 58)2-19已知一实信号x(t)，该信号的最高频率为のm=200rad/s，用のsm=600rad/s对x(t)进行抽样。如对抽样信号做1024点的DFT，试确定Xm|中m=128和m=768点所分别对应的原连续信号的连续频谱点，和の2。解：对连续信号x()以のsam=600rad/s进行抽样，得到离散序列x[k]，由于满足时域抽样定理抽样过程没有出现混迭。在利用序列x[K]的DFTX[m]分析连续信号x()的频谱X(jo)时，从X[m]可以获得X(jの)的对应点频率。当m=128时，由于0≤m≤N/2-1，故有600Qsamm=×128=75rad/s0, =N1024当m=768时，由于N/2≤m≤N-1，故可得600sm(m- N)=0,x(768-1024)=-150rad/s1024NM2-4已知一离散序列x[k]=cos2k+0.75cos2,k，其中2=2元/15rad,2,=2.3元/15rad。(1）对x[Kk做64点FFT，画出其信号的频谱(1）如果(1)中显示的谱不能分辨两个谱峰，是否可对(1)中的64点信号补零而分辨出两个谱峰。通过MATLAB进行证实，并解释其原因。解：（1）利用MATLAB对x[K]做64点FFT的程序及频谱图如下：N=64;30W0=2.0*pi/15.0;25W1=2.3*pi/15.0;20k=(0:N-1);15x=cos(W0*k)+0.75*cos(W1*k)10L=N;5XW=fft(x,L);X=fftshift(XW);03-202-113W=-pi+(0:L-1)*2*pi/L

140 第 3 章 离散傅里叶变换快速算法 y0 [k ] = x0 [k ] Ä h[k ] = {64, 28, 2, 11, 27, 45, 63} y1 [k ] = x1 [k] Ä h[k ] = {150, 105, 81, 99, 117, 135, 153} 2 1 y [k ] = x [k]Ä = h k[ ] {26, 107, 139, 58, 0, 0, 0} 去掉每个 y [k] i 前面的 2 个样本后，把各 y [k] i 依次拼接在一起，即可得到输出序列为 y[k]={ 2, 11, 27, 45, 63, 81, 99, 117, 135, 153, 139, 58} 2-19 已知一实信号 x(t), 该信号的最高频率为w m=200 rad/s, 用w sam=600 rad/s 对 x(t)进行抽 样。如对抽样信号做 1024 点的 DFT，试确定 X[m]中 m=128 和 m=768 点所分别对应的原连续 信号的连续频谱点w 1和w 2。 解：对连续信号 x(t)以wsam=600 rad/s 进行抽样，得到离散序列 x[k]，由于满足时域抽样定理， 抽样过程没有出现混迭。在利用序列 x[k]的 DFT X[m]分析连续信号 x(t)的频谱 X(jw)时，从 X[m] 可以获得 X(jw)的对应点频率。 当 m=128 时，由于0 £ m £ N / 2 -1，故有 sam 1 600 128 75 rad/s 1024 m N w w = = ´ = 当 m=768 时，由于 N / 2 £ m £ N -1，故可得 sam 2 600 ( ) (768 1024) 150 rad/s 1024 m N N w w = - = ´ - = - M2-4 已知一离散序列 x[k]=cosW0k+0.75cos W1k，其中W0=2p/15 rad, W1=2.3p/15 rad。 (1) 对 x[k]做 64 点 FFT, 画出其信号的频谱。 (1) 如果(1)中显示的谱不能分辨两个谱峰，是否可对(1)中的 64 点信号补零而分辨出 两个谱峰。通过 MATLAB 进行证实，并解释其原因。 解：(1) 利用 MATLAB 对 x[k]做 64 点 FFT 的程序及频谱图如下： N=64; W0=2.0*pi/15.0; W1=2.3*pi/15.0; k=(0:N-1); x=cos(W0*k)+0.75*cos(W1*k); L=N; XW=fft(x,L); X=fftshift(XW); w=-pi+(0:L-1)*2*pi/L; -3 -2 -1 0 1 2 3 0 5 10 15 20 25 30

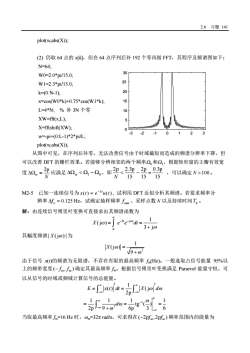
2.6习题141plot(w,abs(X);(2）仍取64点的x[K]，但在64点序列后补192个零再做FFT，其程序及频谱图如下：N=64;30W0=2.0*pi/15.0;25W1=2.3*pi/15.0;20k=(0:N-1);15x=cos(W0*k)+0.75*cos(W1*k)L=4*N:%补3N个零10XW=ff(x,L);5X=fftshift(XW);a0-2-1012-33W=-pi+(O:L-1)*2*pi/L;plot(w,abs(X));从图中可见，在序列后补零，无法改善信号由于时域截短而造成的频谱分辨率下降，但可以改善DFT的栅栏效果。若能够分辨相邻的两个频率2,和2，根据矩形窗的主瓣有效宽即2P、2.3p2p_0.3p只应满足A2100。度2=15NN1515M2-5已知一连续信号为x(t)=e-3u(t)，试利用DFT近似分析其频谱。若要求频率分辨率△f。=0.125Hz，试确定抽样频率fsm、采样点数N以及持续时间T。解：由连续信号傅里叶变换可直接求出其频谱函数为1e-3e-jotdt=X(jo)=3+jo其幅度频谱|X(j)I为1[x(jo)] =/9+02由于信号x(0)的频谱为无限谱，不存在有限的最高频率f(Hz)。一般选取占信号能量95%以上的频带宽度（-fm，f）确定其最高频率fm。根据信号傅里叶变换满足Parsevel能量守恒，可以从信号的时域或频域计算信号的总能量。E=x(0)] dt=x(jo| daOndo=--tg-a9+06p62pJ-当取最高频率=16Hz时，0m=32元rad/s，可求得在（-2pfm，2pfm）频率范围内的能量为

2.6 习题 141 plot(w,abs(X)); (2) 仍取 64 点的 x[k]，但在 64 点序列后补 192 个零再做 FFT，其程序及频谱图如下： N=64; W0=2.0*pi/15.0; W1=2.3*pi/15.0; k=(0:N-1); x=cos(W0*k)+0.75*cos(W1*k); L=4*N; % 补 3N 个零 XW=fft(x,L); X=fftshift(XW); w=-pi+(0:L-1)*2*pi/L; plot(w,abs(X)); 从图中可见，在序列后补零，无法改善信号由于时域截短而造成的频谱分辨率下降，但 可以改善 DFT 的栅栏效果。若能够分辨相邻的两个频率W0和W1，根据矩形窗的主瓣有效宽 度 N 2p DWw = 应满足 DWw 100。 M2-5 已知一连续信号为 ( ) ( ) 3 x t e u t - t = , 试利用 DFT 近似分析其频谱。若要求频率分 辨率 Df c = 0.125 Hz，试确定抽样频率 sam f 、采样点数 N 以及持续时间Tp 。 解：由连续信号傅里叶变换可直接求出其频谱函数为 3 j 0 1 (j ) 3 j t t X e e dt w w w ¥ - - = = + ò 其幅度频谱| X (jw) | 为 2 1 (j ) 9 X w w = + 由于信号 x(t)的频谱为无限谱，不存在有限的最高频率 fm(Hz)。一般选取占信号能量 95%以 上的频带宽度 m m (- f f , ) 确定其最高频率 fm。根据信号傅里叶变换满足 Parsevel 能量守恒，可 以从信号的时域或频域计算信号的总能量。 2 2 1 ( ) ( j 2p E x t dt X d w w ¥ ¥ -¥ -¥ = = ò ò 1 2 1 1 1 1 tg ( ) 2p 9 6p 3 6 d w w w ¥ ¥ - -¥ -¥ = = = + ò 当取最高频率 fm=16 Hz 时，wm=32p rad/s，可求得在 m m ( 2- pf f ,2p ) 频率范围内的能量为 -3 -2 -1 0 1 2 3 0 5 10 15 20 25 30

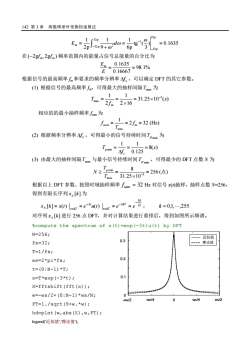
142第3章离散傅里叶变换快速算法/32p132p0E.= 0.1635dotgJ-32p9+@6p2p332在（-2pfm2pfm）频率范围内的能量占信号总能量的百分比为Em0.1635=98.1%E0.16667根据信号的最高频率f和要求的频率分辨率Af。，可以确定DFT的其它参数。(1）根据信号的最高频率fm，可得最大的抽样间隔Tmx为11=31.25×10-(s)Tmax =2fm2x16相应的的最小抽样频率Jsam为1 =2 f =32 (Hz)famT..为(2）根据频率分辨率Af。，可得最小的信号持续时间T，2mi11T= 8(s)0.125Af.(3）由最大的抽样间隔T.与最小信号持续时间T可得最少的DFT点数N为Pmi,Tpmin8N≥=256（点）31.25×10-3Tmax根据以上DFT参数，按照时域抽样频率fsam=32Hz对信号x(t)抽样，抽样点数N=256,得到有限长序列x[k]为3k=e-3KT =e32,r =e-"u(t) /k=0.1.....255xx[k]=x(t)对序列x[K]进行256点DFT，并对计算结果进行重排后，得到如图所示频谱。&computethe spectrum of x(t)=exp(-3t)u(t)byDFTN=256;近似值0.3理论值fs=32;T=1/fs;0.2ws=2*pi*fs;t=(0:N-1)*T;0.1x=T*exp(-3*t);X=fftshift(fft(x));W=-WS/2+(O:N-1)*wS/N;0-Ws/4ws/4-Ws/20Ws/2FT=1./sqrt(9+w.*w);hd=plot(w,abs(X),w,FT);legend(近似值，理论值"）

142 第 3 章 离散傅里叶变换快速算法 32p 32p 1 m 2 32p 32p 1 1 1 tg ( ) 0.1635 2p 9 6p 3 E d w w w - - - = = = + ò 在 m m ( 2- pf f ,2p ) 频率范围内的能量占信号总能量的百分比为 m 0.1635 98.1% 0.16667 E E = » 根据信号的最高频率 fm和要求的频率分辨率 c Df ，可以确定 DFT 的其它参数。 (1) 根据信号的最高频率 fm，可得最大的抽样间隔Tmax 为 3 max m 1 1 31.25 10 ( ) 2 2 16 T s f - = = = ´ ´ 相应的的最小抽样频率 fsam为 m m max 1 2 32 (Hz) sa f f T = = = (2) 根据频率分辨率 c Df ，可得最小的信号持续时间 min Tp 为 min 1 1 8( ) 0.125 p c T s f = = = D (3) 由最大的抽样间隔Tmax 与最小信号持续时间 min Tp ，可得最少的 DFT 点数 N 为 min 3 max 8 256 31.25 10 Tp N T - ³ = = ´ (点) 根据以上 DFT 参数，按照时域抽样频率 32 f sam = Hz 对信号 x(t)抽样，抽样点数 N=256， 得到有限长序列 x [k] N 为 32 3 3 3 [ ] ( ) ( ) k kT t kT t N t kT x k x t e u t e e - - = - = = = = = ， k = 0,1,L,255 对序列 x [k] N 进行 256 点 DFT，并对计算结果进行重排后，得到如图所示频谱。 %compute the spectrum of x(t)=exp(-3t)u(t) by DFT N=256; fs=32; T=1/fs; ws=2*pi*fs; t=(0:N-1)*T; x=T*exp(-3*t); X=fftshift(fft(x)); w=-ws/2+(0:N-1)*ws/N; FT=1./sqrt(9+w.*w); hd=plot(w,abs(X),w,FT); legend('近似值','理论值'); -ws/2 0 0 0.1 0.2 0.3 近似值 理论值 -ws/4 ws/4 ws/2