《数字信号处理》课程教学资源（习题解答）ch5 FIR数字滤波器的设计

5.6习题15.6习题5-1设Fi(a)是线性相位FIR系统函数H(=)的一个因子。试确定满足条件的最低阶的H(=)。(1) F (=) = 1+ 2=- + 3=2(2) F(=) =3 + 5=-l 4z 2 22-3解：设F(=)=a+bz-l+cz-2，则零点为其倒数的多项式Fz()为F,(=)=(a+ bz+cz2 )=- =c+bz-l +az-2(1) H(=)= (1+ 22-* +32)(3+22-* +2~)= 3 +82 +14=2 + 82-* + 32-(2)H(=)=(3+52-1 -42-2 -2z-)(-2 -4z- +5=-2 +3z3)= 6222" +3-~ + 542 +3- 22--5 6-5-2某三阶设FIR滤波器的系统函数Hi(a)为H,(=) =(6 - z-1 -12 2- )(2 + 52-l)(1)试确定幅度响应和H(=)相同的所有FIR滤波器的系统函数。(2)上述FIR滤波器哪个是最大相位系统，哪个是最小相位系统？解：设H(=)=α+bz-是一个实系数的1阶FIR系统，则H(=)=z"H(=")=b+az"是和H(=)幅度响应相同的FIR系统H,(=) =(2 32" )(3 +42-')(2 +52-) =12 + 28≥- - 292-2 602-3(1) H,(=) =(-3 + 2-' )(3 +4z-')(2+ 52-) = -18 57=" 142~ +402-3H,(2) =(2 3-")(4 + 3z-)(2 + 5z") = 16 + 28=-l = 48-2 452-3H,(=) = (2 32")(3 +42)(5 + 22-") = 30 + 72 622 24=-3H, (=) = (3 + 2=- )(4 + 3z~* )(2 + 5=) = 24 62 = + 7= + 30 =-3

5.6 习题 1 5.6 习题 5-1 设 F1(z)是线性相位 FIR系统函数 H(z)的一个因子。试确定满足条件的最低阶的 H(z)。 (1) 1 2 1 ( ) 1 2 3 - - F z = + z + z (2) 1 2 3 1 ( ) 3 5 4 2 - - - F z = + z - z - z 解：设 1 2 1 ( ) - - F z = a + bz + cz ，则零点为其倒数的多项式 ( ) 2 F z 为 2 2 1 2 2 ( ) ( ) - - - F z = a + bz + cz z = c + bz + az (1) ( ) (1 2 3 )(3 2 ) -1 -2 -1 -2 H z = + z + z + z + z 1 2 3 1 3 8 14 8 3 - - - - = + z + z + z + z (2) ( ) (3 5 4 2 )( 2 4 5 3 ) -1 -2 -3 -1 -2 -3 H z = + z - z - z - - z + z + z 1 2 3 4 5 6 6 22 3 54 3 22 6 - - - - - - = - - z + z + z + z - z - z 5-2 某三阶设 FIR 滤波器的系统函数 H1(z)为 ( ) (6 12 )(2 5 ) 1 2 1 1 - - - H z = - z - z + z (1)试确定幅度响应和 H1(z)相同的所有 FIR 滤波器的系统函数。 (2)上述 FIR 滤波器哪个是最大相位系统，哪个是最小相位系统？ 解： 设 1 ( ) - H z = a + bz 是一个实系数的 1 阶 FIR 系统，则 1 1 1 0 H (z) z H ( ) z b az - - - = = + 是和 H z( ) 幅度响应相同的 FIR 系统 1 1 1 1 2 3 1 ( ) (2 3 )(3 4 )(2 5 ) 12 28 29 60 - - - - - - H z = - z + z + z = + z - z - z (1) ( ) ( 3 2 )(3 4 )(2 5 ) 1 1 1 2 - - - H z = - + z + z + z 1 2 3 18 57 14 40 - - - = - - z - z + z ( ) (2 3 )(4 3 )(2 5 ) 1 1 1 3 - - - H z = - z + z + z 1 2 3 16 28 48 45 - - - = + z - z - z ( ) (2 3 )(3 4 )(5 2 ) 1 1 1 4 - - - H z = - z + z + z 1 2 3 30 7 62 24 - - - = + z - z - z ( ) ( 3 2 )(4 3 )(2 5 ) 1 1 1 5 - - - H z = - + z + z + z 1 2 3 24 62 7 30 - - - = - - z + z + z

H,()=(2-3--")(4 +32)(5+2--)= 40 142 572-218--3H,(=)=(-3 +2--)(3+4z")(5 + 2z) =45 48- +282 +16-H,(=)=(-3+2z")(4+3z)(5+2z) =-60-29z- +282- +122-(2) H,(=)=(2-3=)(3+4=）(2+5=-"）是最大相位系统H(=)=（-3+2="）4+3=-）5+22-"）是最小相位系统5-3已知8阶I型线性相位FIR滤波器的部分零点为：z1=2，22=j0.5，3-j(1)试确定该滤波器的其他零点。(2)设h[0]=1,求出该滤波器的系统函数H(a)。解:(1)z4=1/ z/=1/2;25=1/ 22=-j2,26=22=-j0.5, 27-25-j2≥8=1/ 23= -j(2)H(=)= (1-==)=1+ 8-2.5(+ 27)+6.25(22+ 26)-13.125(-3+ -5)+10.5 5-4已知9阶ⅡI型线性相位FIR滤波器的部分零点为：=1=2，22=j0.5，23-j(1)试确定该滤波器的其它零点。(2)设h[0]=1，求出该滤波器的系统函数H()。解(1)z4=1/ =/=1/2;z5=1/ 22= -j2,z6==2'= -j0.5, 27-z5=j2;≥8=1/ 3= j,29= -1;(2)H(=)= (1-=)=1+ 29-1.5(2'+ 8)+3.75(-2+ 7)- 6.875 (3+ 2) -2.625(2*+ 25)5-5已知8阶IⅡII型线性相位FIR滤波器的部分零点为：2=-0.2，22=j0.8(1)试确定该滤波器的其他零点。(2)设h[0]=1,求出该滤波器的系统函数H(=)。解：(1)23=1/ 2,--5;

( ) (2 3 )(4 3 )(5 2 ) 1 1 1 6 - - - H z = - z + z + z 1 2 3 40 14 57 18 - - - = - z - z - z ( ) ( 3 2 )(3 4 )(5 2 ) 1 1 1 7 - - - H z = - + z + z + z 1 2 3 45 48 28 16 - - - = - - z + z + z ( ) ( 3 2 )(4 3 )(5 2 ) 1 1 1 8 - - - H z = - + z + z + z 1 2 3 60 29 28 12 - - - = - - z + z + z (2) ( ) (2 3 )(3 4 )(2 5 ) 1 1 1 1 - - - H z = - z + z + z 是最大相位系统 ( ) ( 3 2 )(4 3 )(5 2 ) 1 1 1 8 - - - H z = - + z + z + z 是最小相位系统 5-3 已知 8 阶 I 型线性相位 FIR 滤波器的部分零点为：z1=2，z2=j0.5，z3=j (1)试确定该滤波器的其他零点。 (2)设 h[0]=1, 求出该滤波器的系统函数 H(z)。 解: (1)z4=1/ z1=1/2; z5=1/ z2= -j2，z6=z2 * = -j0.5，z7=z5 * = j2； z8=1/ z3= -j (2) ( ) (1 ) 1 8 1 k k H z z z - = = Õ - =1+ z -8 -2.5(z -1 + z -7 )+6.25(z -2 + z -6 )-13.125(z -3 + z -5 )+10.5 z -4 5-4 已知 9 阶 II 型线性相位 FIR 滤波器的部分零点为：z1=2，z2=j0.5，z3=-j (1)试确定该滤波器的其它零点。 (2)设 h[0]=1, 求出该滤波器的系统函数 H(z)。 解: (1)z4=1/ z1=1/2; z5=1/ z2= -j2，z6=z2 * = -j0.5，z7=z5 * = j2； z8=1/ z3= j; z9= -1; (2) ( ) (1 ) 1 9 1 k k H z z z - = = Õ - =1+ z -9 -1.5(z -1 + z -8 )+3.75(z -2 + z -7 )- 6.875 (z -3 + z -6 ) -2.625(z -4 + z -5 ) 5-5 已知 8 阶 III 型线性相位 FIR 滤波器的部分零点为：z1= -0.2，z2=j0.8 (1)试确定该滤波器的其他零点。 (2)设 h[0]=1, 求出该滤波器的系统函数 H(z)。 解: (1)z3=1/ z1=-5;

5.6习题3z4=1/22=-j1.25,zs=z2 =-j0.8,z6=z4 = j1.25;27= -1;≥8= 1;H(=)=(2)Z.ke=128+5.2(-17)+2.2025 (2-)- 6.253 (-3-25)5-6已知9阶IV型线性相位FIR滤波器的部分零点为：2=-1，22=0.8，23=0.5j，(1)试确定该滤波器的其他零点。(2)设h[0]-1,求出该滤波器的系统函数H(=)。解：(1)z4=1/ 22=1.25;z5=1/ 23= -j2,26=23 =-j0.5, 27=z5 = j2;28=21= -1;z9= 1;(2)H(=)=I (1-==)=1- 21.05 (21- 28)+ 2.2 (2- 7)- 2.4125 (3- 26) -6.6625(24- 25)5-7试证明式(5-7)和式(5-8)。证：M/2-1H(e"°)=217h[k]e-soh[k]e-ji + h[M / 2]e-i(M/2)0 +h[k]e-ikNk=01-0k=M /2+1令l=M-k，则有M/2-1M/2-h[M-]]e-i(M-1)2h[k]e-i(M-k)ah[k]e-nnWK=0k=M/2+l所以H(ej°)=e-(M/2)n[)[e-ie ;(M2)0 +e-(M/2-0) ]+[M /2]=e-j(M2)n2 h[k]cos[(0.5M-k)2]+h[M /2]=MI2=e-(M/2)n2h[0.5M -k]cos(k2)+h[M /2]>k=记：L=M/2，则有A2h[L-k]cos(k2)+h[L]A(2)=)?21=IH(ej0)=e-(M/2) A(2)

5.6 习题 3 z4=1/ z2= -j1.25，z5=z2 * = -j0.8，z6=z4 * = j1.25； z7= -1; z8= 1; (2) ( ) (1 ) 1 8 1 k k H z z z - = = Õ - =1- z -8 +5.2(z -1 - z -7 )+ 2.2025 (z -2 - z -6 )- 6.253 (z -3 - z -5 ) 5-6 已知 9 阶 IV 型线性相位 FIR 滤波器的部分零点为：z1= -1，z2=0.8，z3= 0.5j， (1)试确定该滤波器的其他零点。 (2)设 h[0]=1, 求出该滤波器的系统函数 H(z)。 解: (1)z4=1/ z2=1.25; z5=1/ z3= -j2，z6=z3 * = -j0.5，z7=z5 * = j2； z8=z1= -1; z9= 1; (2) ( ) (1 ) 1 9 1 k k H z z z - = = Õ - =1- z -9 -1.05 (z -1 - z -8 )+ 2.2 (z -2 - z -7 )- 2.4125 (z -3 - z -6 ) -6.6625(z -4 - z -5 ) 5-7 试证明式(5-7)和式(5-8)。 证： W W W W kW M k M k M M k k M k H h k h k h M h k j /2 1 j j( /2 ) /2 1 0 j 0 j (e ) [ ]e [ ]e [ / 2]e [ ]e - = + - - - = - = = å = å + + å 令l = M - k ，则有 W W j( ) W /2 1 0 j( ) /2 1 0 j /2 1 [ ]e [ ]e [ ]e M k M k M l M l k M k M h k h M l h k - - - = - - - = - = + å = å - = å 所以 [ ] þ ý ü î í ì = + + - - - - = - (e ) e å [ ] e e e [ / 2] j j( 2 ) j( / 2 ) /2 1 0 j j( / 2 ) H h k h M k M/ M k M k W M W W W W [ ] þ ý ü î í ì = å - + - = - e 2 [ ]cos (0.5 ) [ / 2] /2 1 0 j( /2 ) h k M k h M M k M W W þ ý ü î í ì = å - + = - e 2 [0.5 ]cos( ) [ / 2] /2 1 j( / 2 ) h M k k h M M k M W W 记：L=M/2，则有 ( ) 2 [ ]cos( ) [ ] 1 A h L k k h L L k = å - + = W W (e ) e ( ) j j( / 2) W W W H A - M =

5-8试证明式(5-10)和式(5-11)。证：M--)/2学H(ei°)=2h[k]e-jkah[k ]e-inh[k]e-jia7k=01=0k=(M+1)2令l=M-k，则有(M-1V2(M-1)/2产Z h[k Je-i(M- )n2 h[M-1]e-i(M-1)2h[k]e-ik?0k=(M+1)/2所以[(M-)/2h[[e-ej(M2) +e-(M/2-k)=e-(M/2)QIH(ejn)k=0=e-j(M2)o(M-)22h[k]cos[(0.5M -k)2]2(M-1)/2=ej(M/2)02h[K]cos[(M -1)/2 - k+0.5)2]NE(M-1)/2=e-(M/2)Q2 h[(M -1)/2- k]cos[(k + 0.5) 2)]7keo记：L=(M-1)/2，则有A(2)=≥2h[L-k]cos[(k+0.5)2]=0H(ejg)=e-(M/2)2 A(2)5-9试证明式(5-13)和式(5-14)。证：对III型线性相位系统，h[M/2]=0，所以M /21MMh[k]e-knh[k]e-ia +h[k]e-jikaH(ejn)=)k-01-0k=M/2+1令l=M-k，则有2M/2-M/2-Ih[k]e-jh[M -/]e-i(M-1)2h[kJe-j(M-k)a>>10A=0A=M/2+I所以112-H(ejQ)=e-(M/2)Qh[ke-iej2)a-e~(M/2-t)0212=e-(M/2)n2jh[k ]sin [(0.5M-k)2]2N=e-j(M/2)42jh[0.5M-k|sin(kQ)2记：L=M/2，则有

5-8 试证明式(5-10)和式(5-11)。 证： W W W kW M k M k M k k M k H h k h k h k j ( 1 )/ 2 j ( 1 ) /2 0 j 0 j (e ) [ ]e [ ]e [ ]e - = + - - = - = = å = å + å 令l = M - k ，则有 W W j( )W ( 1 )/ 2 0 j( ) ( 1 ) /2 0 j ( 1) / 2 [ ]e [ ]e [ ]e M k M k M l M l k M k M h k h M l h k - - - = - - - = - = + å = å - = å 所以 [ ] þ ý ü î í ì = + - - - - = - å W W j W j( 2) W j( /2 )W ( 1)/2 0 j j( / 2) (e ) e [ ] e e e k M/ M k M k M H h k [ W ] W e 2 [ ]cos (0.5 ) ( 1) /2 0 j( /2) h k M k M k M = å - - = - [( )W ] W e 2 [ ]cos ( 1)/ 2 0.5 ( 1) /2 0 j( / 2) = å - - + - = - h k M k M k M e 2 [( 1)/ 2 ]cos[( 0.5) )] ( 1) /2 0 j( / 2) W W = å - - + - = - h M k k M k M 记：L=(M-1)/2，则有 ( ) 2 [ ]cos[( 0.5) )] 0 W = å - + W = A h L k k L k (e ) e ( ) j j( / 2) W W W H A - M = 5-9 试证明式(5-13)和式(5-14)。 证： 对 III 型线性相位系统，h[M/2]=0，所以 W W W kW M k M k M k k M k H h k h k h k j / 2 1 j / 2 1 0 j 0 j (e ) [ ]e [ ]e [ ]e - = + - - = - = = å = å + å 令l = M - k ，则有 W W j( ) W /2 1 0 j( ) /2 1 0 j /2 1 [ ]e [ ]e [ ]e M k M k M l M l k M k M h k h M l h k - - - = - - - = - = + å = å - = - å 所以 [ ] W W j W j( 2) W j( / 2 ) W / 2 1 0 j j( / 2) (e ) e [ ] e e e k M/ M k M k M H h k - - - - = - = å - [ W ] W e 2j [ ]sin (0.5 ) /2 1 0 j( / 2) h k M k M k M = å - - = - e 2j [0.5 ]sin( ) /2 1 j( /2) W W h M k k M k M = å - = - 记：L=M/2，则有

5.6习题5A(2)=2 2h[L-k]sin(k2)1=lH(ej0)=e-(M/2)em/2 A(2)5-10试证明式(5-16）和式(5-17)。证：( M)/2H(eja)=^Mh[k]e-ioZ h[k]e-inh[k ]e-ikak=0k=0k=(M+1V2令1=M-k，则有(M-)/2(M-1)/2AZ h[k]e-i(M-1)ah[M - 1]e-i(M-1)2h[k]e-ikaM1=010k=(M+1)/2所以-j(M/2)Q-j(M /2-k)-jQj(M/2)Oh[keH(e>1-0(M-1)/2=e(M/2)Q2jh[k ]sin [(0.5M - k)2]Mk=0(M1)/2=e-j(M/2)o2jh[k]sin [(M -1) /2 -k +0.5)2]A=0(M-1)/2=e-j(M2)02jh[(M -1) /2-k]sin[(k + 0.5)2)]2k=0记：L=(M-1)/2，则有2h[L-k]sin[(k +0.5)2]A(2) =1=0H(eig)=e-(M/2)aem/2 A(2)5-11Hi(=)、H2()、Hs(=)和H4(=)分别表示I型、IⅡI型、IⅡII型和IV型线性相位FIR滤波器，试判断下列级联是否为线性相位系统？如是线性相位系统试确定其类型。(1)Gi()= Hi() H(日)(2) G2(2)= H(=) H(=)(3) G;(2)= H() H(=)(4)G4(=)= Hi() H4(=)(5) Gs(=)=H2() H2(=) (6) G6(=)= H2() Hs(=)(7)G(=)= H2(=) H4(=) (8) Gs(=)= Hs() Hs(=) (9) Gg(=)= Hs(=) H4(=)(10)G10(=)= H4(=) H4(=)解：设 Hi()、H2(=)、Hs(=)和 H4(2)的阶数分别为 K(偶数)、L(奇数)、M(偶数)与 N(偶数)(1)-(K+G(=")= 2-*H(=") -*H(=")= H(+) H()= G(c)由于2K为偶数，所以是I型线性相位系统(2) -(K+D)G2(=-")= *H;(=") ="H2(=-")= Hi() H2(2)= G2()由于K+L为奇数，所以是II型线性相位系统

5.6 习题 5 ( ) 2 [ ]sin( ) 1 A W h L k kW L k = å - = (e ) e e ( ) j j( / 2) j / 2 W W W H A - M p = 5-10 试证明式(5-16) 和式(5-17)。 证： W W W kW M k M k M k k M k H h k h k h k j ( 1 )/ 2 j ( 1 ) /2 0 j 0 j (e ) [ ]e [ ]e [ ]e - = + - - = - = = å = å + å 令l = M - k ，则有 W W j( ) W ( 1) / 2 0 j( ) ( 1 ) /2 0 j ( 1) / 2 [ ]e [ ]e [ ]e M k M k M l M l k M k M h k h M l h k - - - = - - - = - = + å = å - = - å 所以 [ ] þ ý ü î í ì = - - - - - = - å W W j W j( 2) W j( /2 ) W ( 1)/ 2 0 j j( / 2) (e ) e [ ] e e e k M/ M k M k M H h k [ W ] W e 2j [ ]sin (0.5 ) ( 1) /2 0 j( /2) h k M k M k M = å - - = - [( )W ] W e 2 j [ ]sin ( 1)/ 2 0.5 ( 1) /2 0 j( /2) = å - - + - = - h k M k M k M e 2j [( 1) / 2 ]sin [( 0.5) )] ( 1) / 2 0 j( /2 ) W W = å - - + - = - h M k k M k M 记：L=(M-1)/2，则有 ( ) 2 [ ]sin [( 0.5) )] 0 W = å - + W = A h L k k L k (e ) e e ( ) j j( / 2) j / 2 W W W H A - M p = 5-11 H1(z)、H2(z)、H3(z)和 H4(z)分别表示 I 型、II 型、III 型和 IV 型线性相位 FIR 滤波器， 试判断下列级联是否为线性相位系统？如是线性相位系统试确定其类型。 (1)G1(z)= H1(z) H1(z) (2) G2(z)= H1(z) H2(z) (3) G3(z)= H1(z) H3(z) (4)G4(z)= H1(z) H4(z) (5) G5(z)= H2(z) H2(z) (6) G6(z)= H2(z) H3(z) (7)G7(z)= H2(z) H4(z) (8) G8(z)= H3(z) H3(z) (9) G9(z)= H3(z) H4(z) (10)G10(z)= H4(z) H4(z) 解: 设 H1(z)、H2(z)、H3(z)和 H4(z)的阶数分别为 K(偶数)、L(奇数)、M(偶数)与 N(偶数) (1)z -(K+K)G1(z -1 )= z -KH1(z -1 ) z -KH1(z -1 )= H1(z) H1(z)= G1(z) 由于 2K 为偶数，所以是 I 型线性相位系统 (2) z -(K+L)G2(z -1 )= z -KH1(z -1 ) z -LH2(z -1 )= H1(z) H2(z)= G2(z) 由于 K+L 为奇数，所以是 II 型线性相位系统

(3) 2(K+MG(=')= =*HI(=") =MH(=")= -Hi() H(2)=- G(2)由于K+M为偶数，所以是I型线性相位系统(4) 2-(K+MG4(")= 2-*Hi(=") =NH4(=")= -H() H4(2)= -G4(2)由于K+N为奇数，所以是IV型线性相位系统(5) 2-(L+D)G;(2")= 2"H2(=") 2"H2(')= H2(=) H2(=)= Gs(2)由于2L为奇偶数，所以是I型线性相位系统(6)-(L+MG(2)=2*H(=) -MH(=)= -H2() H()= -G(2)由于L+M为奇数，所以是IV型线性相位系统(7) =(+MG(=")= *H2(=") =NH4(=")= -H2() H4(2)= -G(2)由于K+N为偶数，所以是III型线性相位系统(8) 2-(N+MGs(=")= 2NH;(2) NH(=)= H() H;()= Gg()由于2K为偶数，所以是I型线性相位系统(9) 2(M+MG(=)= 2MH(2) 2NH4(2)= Hs() H(2)= G(2)由于M+N为奇数，所以是II型线性相位系统(10) 2(N+MG10(2)= 2NH4() NH4()- H4(2) H4(=)= G10(2)由于2N为奇偶数，所以是I型线性相位系统5-12试用矩形窗设计一个线性相位FIR带通滤波器，要求其频率响应逼近a-jaf，2±22H,(ejn)=0其它(1)h[k]可以是哪几种线性相位滤波器？(2)求出h[k]的表达式，确定α与M的关系。(3)当M=8，2=0.1元，20=0.6元时，求出用矩形窗和哈明窗设计的滤波器的幅度函数并画出它们的波形。解：(1)h[k]可以是I型和 ⅡI 型线性相位滤波器。(2) α=M/2dha[k]H.(e2元Qo-+0ejk-an dQ-(k-a)ad-2,+0021 sin [(k -α)(。 +2.]- sin [(k -α)(2。 -2)](k-α)

(3) z -(K+M)G3(z -1 )= z -KH1(z -1 ) z -MH3(z -1 )= -H1(z) H3(z)=- G3(z) 由于 K+M 为偶数，所以是 III 型线性相位系统 (4) z -(K+N)G4(z -1 )= z -KH1(z -1 ) z -NH4(z -1 )= -H1(z) H4(z)= -G4(z) 由于 K+N 为奇数，所以是 IV 型线性相位系统 (5) z -(L+L)G5(z -1 )= z -LH2(z -1 ) z -LH2(z -1 )= H2(z) H2(z)= G5(z) 由于 2L 为奇偶数，所以是 I 型线性相位系统 (6)z -( L+M)G6(z -1 )= z -LH2(z -1 ) z -MH3(z -1 )= -H2(z) H3(z)= -G6(z) 由于 L+M 为奇数，所以是 IV 型线性相位系统 (7) z -(L+N)G7(z -1 )= z -KH2(z -1 ) z -NH4(z -1 )= -H2(z) H4(z)= -G7(z) 由于 K+N 为偶数，所以是 III 型线性相位系统 (8) z -(N+N)G8(z -1 )= z -NH3(z -1 ) z -NH3(z -1 )= H3(z) H3(z)= G8(z) 由于 2K 为偶数，所以是 I 型线性相位系统 (9) z -(M+N)G9(z -1 )= z -MH3(z -1 ) z -NH4(z -1 )= H3(z) H4(z)= G9(z) 由于 M+N 为奇数，所以是 II 型线性相位系统 (10) z -(N+N)G10(z -1 )= z -NH4(z -1 ) z -NH4(z -1 )= H4(z) H4(z)= G10(z) 由于 2N 为奇偶数，所以是 I 型线性相位系统 5-12 试用矩形窗设计一个线性相位 FIR 带通滤波器，要求其频率响应逼近 î í ì ± < = - 0 . e , (e ) 0 j j d 其它 c H W W W aW W (1)h[k]可以是哪几种线性相位滤波器？ (2)求出 h[k]的表达式，确定a与 M 的关系。 (3)当 M=8，Wc=0.1p，W0=0.6p时，求出用矩形窗和哈明窗设计的滤波器的幅度函数 并画出它们的波形。 解： (1) h[k]可以是 I 型和 II 型线性相位滤波器。 (2) a=M/2 W p = W W p -p ò (e )e d 2 1 [ ] j j d d k h k H ú ú û ù ê ê ë é W - W p = - W W -W -W +W - W W +W -W -W ò ò e d e d 2 1 j( ) j( ) 0 c 0 c 0 c 0 c k a k a [ ] [ ] ú û ù ê ë é - - W + W - - W - W p = ( ) 1 sin ( )( ) sin ( )( ) 0 c 0 c a a a k k k

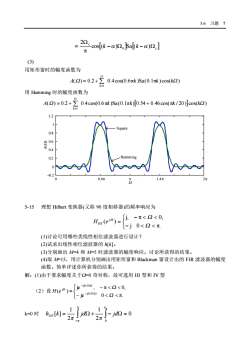
5.6习题722cos[(k -α)2。Fa[k-a)2. ](3)用矩形窗时的幅度函数为15A(2)=0.2+)0.4cos(0.6元k)Sa(0.1元k)cos(k)k=l用Hamming时的幅度函数为0.4cos(0.6元k)Sa(0.1元k)[0.54+0.46cos(元k/20)|cos(k2)A(2)=0.2+1.2ISquare0.8NOC0.4nming0.200.6元1.4元2元5-15理想Hilbert变换器（又称90度相移器）的频率响应为元2<0Hur(ejQ)0<2<元(1)讨论可用哪些类线性相位滤波器进行设计？(2)试求出线性相位滤波器的[]。(3)分别画出M-4和M=5时滤波器的幅度响应。讨论所获得的结果。(4)取M-15，用计算机分别画出用矩形窗和Blackman窗设计出的FIR滤波器的幅度函数。简单评述你所获得的结果。解：（1)由于要求幅度关于=0奇对称，故可选用I型和IV型je -j0.5NQ-元<Q<0(2）设H(ejne-j0.5NQ0<<元dQ=0k=0 时hur[k]idQ2元2元

5.6 习题 7 [ ] [ ] 0 c c cos ( ) Sa ( ) 2 - W - W p W = k a k a (3) 用矩形窗时的幅度函数为 ( ) 0.2 0.4cos(0.6 )Sa(0.1 ) cos( ) 15 1 A W k k kW k = + å p p = 用 Hamming 时的幅度函数为 ( ) 0.2 0.4cos(0.6 )Sa(0.1 )[0.54 0.46cos( / 20)]cos( ) 15 1 A W k k k kW k = + å p p + p = 0 0.6p p 1.4p 2p -0.2 0 0.2 0.4 0.6 0.8 1 1.2 W A(W) Square Hamming 5-15 理想 Hilbert 变换器(又称 90 度相移器)的频率响应为 î í ì - < < p - p < < = j 0 . j, 0, ( ) HT W jW W H e (1)讨论可用哪些类线性相位滤波器进行设计？ (2)试求出线性相位滤波器的 h[k]。 (3)分别画出 M=4 和 M=5 时滤波器的幅度响应。讨论所获得的结果。 (4)取 M=15，用计算机分别画出用矩形窗和 Blackman 窗设计出的 FIR 滤波器的幅度 函数。简单评述你所获得的结果。 解：(1)由于要求幅度关于W=0 奇对称，故可选用 III 型和 IV 型 （2）设 î í ì - < < p - p < < = - - je 0 . je , 0, ( ) j0.5 j0.5 W W W W W N N j H e k=0 时 0 2 1 2 1 [ ] 0 0 = W + - W = ò ò - h k jd jd c HT p p p p

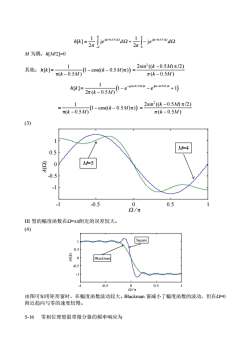
e-n[-jea-0.5s)n doh[k] =2元27M为偶，h[M/2]=01(1-cos(k0.5M)) _2sin(k-0.5M) 元/2)其他：h[K]=元(k-0.5M)元(k-0.5M)1(1 e~ji(4-0.5M)-exk-0.5M)* + 1h[k]= 2元(k-0.5 M)(2sin*((k-0.5M)元/2)(1-cos(k-0.5M)元) =3元（k-0.5M元(k-0.5M)(3)-M=40.5M=5(0))0I-0.5-1-1-0.500.512/元II型的幅度函数在Q=±元附近的误差较大。(4)Square0.5(0)V0Blackman-0.50-0.50.5-1Q/元由图可知用矩形窗时，在幅度函数波动较大。Blackman窗减小了幅度函数的波动，但在Q=0附近趋向与零的速度较慢。5-16零相位理想限带微分器的频率响应为

W p W p p W p W h k e d e d k N k N ò ò - - - = + - 0 j( 0.5 ) 0 j( 0.5 ) j 2 1 j 2 1 [ ] M 为偶，h[M/2]=0 其他： ( ) 1 [ ] 1 cos(( 0.5 ) ) ( 0.5 ) h k k M k M = -p p - 2 2sin (( 0.5 ) /2) ( 0.5 ) k M p k M - p = - ( ) 1 j( 0.5 ) j( 0.5 ) [ ] 1 e e 1 2 ( 0.5 ) k M k M h k p k M - - p - p = - - + - ( ) 1 1 cos(( 0.5 ) ) ( 0.5 ) k M k M = -p p - 2 2sin (( 0.5 ) /2) ( 0.5 ) k M p k M - p = - (3) -1 -0.5 0 0.5 1 -1 -0.5 0 0.5 1 M=4 M=5 A(W) W / p III 型的幅度函数在W=±p附近的误差较大。 (4) -1 -0.5 0 0.5 1 -1 -0.5 0 0.5 1 Blackman Square W / p A(W) 由图可知用矩形窗时，在幅度函数波动较大。Blackman 窗减小了幅度函数的波动，但在W=0 附近趋向与零的速度较慢。 5-16 零相位理想限带微分器的频率响应为

5.6习题9HaLpr(e10)-[j2, [2/<2.,2<2<p0试确定该系统的单位脉冲响应hBLDIr[K]。解：HBLDIr(ein)=j2[u(2+2)-u(2-2)]H"BLpir(ein)=j[u(2+2.)-u(2 -2. )]+j2.[-8(2+2.)-8(2-2.)]jH"BDIr(ej°)=-[u(2+2.)- u(2-2,)]+2.[6(2+2.)+8(2-2.)]2k[k]=-[" ed2+2,[e-in, +en, ][e4o. -ej0. +2.[e-o: +e/0. --2sin(2.k)+22. cos(2.k)kikhalor[k]= - sin(2.k) , 2. cos(2,k)元k?元k5-17零相位理想线性通带低通滤波器的频率响应为J12], [2]<2e,HLLp(e)=02 <2<元试确定该系统的单位脉冲响应hup[k]。解：H'p(ei )=-[u(2 +2.)-u(2)]+[u(2)-u(Q-2.)]+2.[6(2+2.)-8(2-2.)]jH'up(ei)=-j[u(2 +2.)- u(2)]+j[u(2)-u(2-2, )]+ j2.[6(2+2.)-8(2-2.)]2kk]=-j。ewnd2+jfe eknd2+ j2,[e-in.-exn,]=-jf e-in d2 +jf ein d2-j2.[exo. -e-ko. ]=-2) sin(k2)d2+2sin(k2.)=2(cos(k2.)-1)+22. sin(k2.)khur[(1 -c0s(2.)-1+2. im(2.]; 0, hur[0] -元k2元k2元

5.6 习题 9 î í ì < < < = 0 p. j , , (e ) c j c BLDIF W W W W W W H 试确定该系统的单位脉冲响应 [ ] BLDIF h k 。 解： (e ) j [ ( ) ( )] j BLDIF c c H W u W W u W W W = + - - ' (e ) j[ ( ) ( )] j [ ( ) ( )] j BLDIF c c c c c H u W W u W W W d W W d W W W = + - - + - + - - j ' (e ) [ ( ) ( )] [ ( ) ( )] j BLDIF c c c c c H u W W u W W W d W W d W W W = - + - - + + + - [ ] c c j j j 2 [ ] e d e e W W W W W p W W k k c c k c kh k = - + + - ò- [ ] [ ] c c c c j j j j e e e e 1 W W W W W k k c k k jk = - - + + - - sin( ) 2 cos( ) 2 c k c k k = - W + Wc W k k k k h k c p + p = - sin( ) cos( ) [ ] c 2 c BLDIF W W W 5-17 零相位理想线性通带低通滤波器的频率响应为 î í ì < < < = 0 . , , ( ) LLP W W p W W W W c j c H e 试确定该系统的单位脉冲响应 [ ] LLP h k 。 解： ' (e ) [ ( ) ( )] [ ( ) ( )] [ ( ) ( )] j LLP c c c c c H u W W u W u W u W W W d W W d W W W = - + - + - - + + - - j ' (e ) j[ ( ) ( )] j[ ( ) ( )] j [ ( ) ( )] j LLP c c c c c H u W W u W u W u W W W d W W d W W W = - + - + - - + + - - [ ] c c j j j 0 j 0 2 [ ] e d e d e e W W W W W W p W W W k k c k k kh k j j j c c = - + + - - ò- ò [ ] c c j j j 0 j 0 e d e d e e W W W W W W W W W k k c k k j j j c - c - = - ò + ò - - 2 sin( )d 2sin( ) c 0 W W W W k k c = - ò + (cos( ) 1) 2 sin( ) 2 kWc W kWc k = - + c ; 0 cos( ) 1 sin( ) [ ] c 2 c LLP ¹ p W W + p W - = k k k k k h k c ， p W = 2 [0] 2 LLP c h

5-23已知18阶III型线性相位FIR滤波器的幅度函数满足m=3,4,52元mA0m=0,1,2,6,7,8,919试求出h[K]的表达式。解：Ha[m]的取值为：18元318 xx418元x5191919H,[3] = jeH,[4]= jeH,[5] = je.18元x318 #x418 mxd1919，19，H, [16]= -jeH,[15]= -jeH,[14]= -jem取其他值时Ha[m]=0。对Ha[m]做19点IDFT可得2(2元×322元×422元×5(k-9)(k-9)(k-9)h[k] =sinsinsin-191919191919

5-23 已知 18 阶 III 型线性相位 FIR 滤波器的幅度函数满足 î í ì = = =÷ ÷ ø ö ç ç è æ p 0 0,1,2,6,7,8,9 1, 3,4,5 19 2 m m m A 试求出 h[k]的表达式。 解：Hd[m]的取值为： 19 18 3 j [3] je p´ - = Hd ， 19 18 4 j [4] je p´ - = Hd ， 19 18 5 j [5] je p´ - = Hd 19 18 3 j [16] je p´ = - Hd ， 19 18 4 j [15] je p´ = - Hd ， 19 18 4 j [14] je p´ = - Hd m 取其他值时 Hd[m]=0。对 Hd[m]做 19 点 IDFT 可得 ÷ ø ö ç è æ - ´ ÷ - ø ö ç è æ - ´ ÷ - ø ö ç è æ - ´ = - ( 9) 19 2 5 sin 19 2 ( 9) 19 2 4 sin 19 2 ( 9) 19 2 3 sin 19 2 h[k] k k k p p p