《高频电子线路》课程教学资源（试卷习题）第四章 习题解答

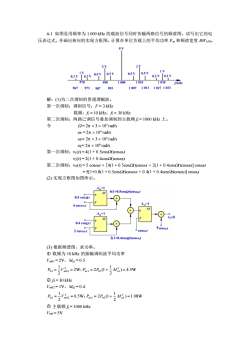
4-1如图是用频率为1000kHz的载波信号同时传输两路信号的频谱图。试写出它的电压表达式，并画出相应的实现方框图。计算在单位负载上的平均功率P和频谱宽度BWAM。5VIV1V0.5V0.5V0.5V50.2V0.2V101010309709901000IkHz1027103396797399310071013987解：（1)为二次调制的普通调幅波。第一次调制：调制信号：F=3kHz载频：fi=10kHz，fz=30kHz第二次调制：两路已调信号叠加调制到主载频f=1000kHz上。令Q=2元×3×10rad/s01=2元×10°rad/s0=2元×3×10°rad/s0= 2元 × 10%rad/s第一次调制：vi(0)=4(1+0.5cos2t)coso)tv2(0)=2(1+0.4cos.2t)cos(02t第二次调制：vo(t)=5coso:1+[4(1+0.5cos.21)cos0i1+2(1+0.4cos2t)cos(1]cos(ol=5[1+0.8(1+0.5cos.52)cosoit+0.4(1+0.4cos-21)coso2t] coso1(2)实现方框图如图所示。A=14(1+0.5cosQt)co5o)txy0.5cosQt+AM=14coso1tAM=1of0.4cos2t5cosct2cosotocosot2(1+0.4cos.2t)coso)t(3)根据频谱图，求功率。①载频为10kHz的振幅调制波平均功率Vmo1=2V,Mai=0.51 v21Poi=Ma)=4.5WV20 =2W; Pav/=2Pol(1+2f2=30kHzVm02=1V，Ma2=0.41 v2M2)=1.08WPo2=V202=0.5W;Pav2=2Po2(1+}22主载频f=1000kHzVmo=5V

4-1 如图是用频率为 1 000 kHz 的载波信号同时传输两路信号的频谱图。试写出它的电 压表达式，并画出相应的实现方框图。计算在单位负载上的平均功率 Pav 和频谱宽度 BWAM。 解：(1)为二次调制的普通调幅波。 第一次调制：调制信号：F = 3 kHz 载频：f1 = 10 kHz，f2 = 30 kHz 第二次调制：两路已调信号叠加调制到主载频 fc = 1000 kHz 上。 令  = 2  3  103 rad/s 1 = 2  104 rad/s 2= 2  3  104 rad/s c= 2  106 rad/s 第一次调制：v1(t) = 4(1 + 0.5cost)cos1t v2(t) = 2(1 + 0.4cost)cos2t 第二次调制：vO(t) = 5 cosct + [4(1 + 0.5cost)cos1t + 2(1 + 0.4cost)cos2t] cosct = 5[1+0.8(1 + 0.5cost)cos1t + 0.4(1 + 0.4cost)cos2t] cosct (2) 实现方框图如图所示。 (3) 根据频谱图，求功率。 ○1 载频为 10 kHz 的振幅调制波平均功率 Vm01 = 2V，Ma1 = 0.5 ) 4.5W 2 1 2W 2 (1 2 1 2 av1 0 1 a1 2 P0 1 = Vm0 1 = ；P = P + M = ○2 f2 = 30 kHz Vm02 = 1V，Ma2 = 0.4 ) 1.08W 2 1 0.5W 2 (1 2 1 2 av2 0 2 a2 2 P0 2 = Vm0 2 = ；P = P + M = ○3 主载频 fc = 1000 kHz Vm0 = 5V

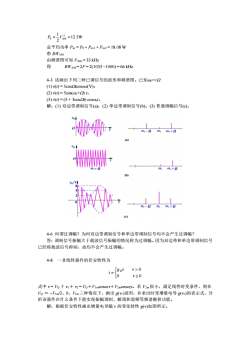
=12.5WP==mo.总平均功率Pav=Po+Pav1+Pav2=18.08W@BWAM由频谱图可知Fmax=33kHz得BWAM=2F=2(1033-1000)=66kHz4-3试画出下列三种已调信号的波形和频谱图。已知0>>Q(1)(t)=5costcosa(V);(2) (t)=5cos(a+2) t;(3) (1)=(5 + 3cos521) cosat。解：（1)双边带调制信号(a)：(2)单边带调制信号(b)：(3)普通调幅信号(c)。HA0+Q(a)0+QWe(b)o/V0+0We(c)4-6何谓过调幅？为何双边带调制信号和单边带调制信号均不会产生过调幅？答：调制信号振幅大于载波信号振幅的情况称为过调幅。因为双边带和单边带调制信号已经将载波信号抑制，故均不会产生过调幅。4-83一非线性器件的伏安特性为v>0[gpylov≤0式中v=Vo十Vi十V2=Vo十VimcoS0it+V2mCoSo2t。若V2m很小，满足线性时变条件，则在V=-Vim/2、0、Vim三种情况下，画出g(vi)波形，并求出时变增量电导g(v)的表示式，分析该器件在什么条件下能实现振幅调制、解调和混频等频谱搬移功能。解：根据伏安特性画出增量电导随的变化特性g(v)如图所示

12.5W 2 1 2 P0 = Vm0 = 总平均功率 Pav = P0 + Pav1 + Pav2 = 18.08 W ○4 BWAM 由频谱图可知 Fmax = 33 kHz 得 BWAM = 2F = 2(1033 −1000) = 66 kHz 4-3 试画出下列三种已调信号的波形和频谱图。已知c>> (1) v(t) = 5costcosct(V)； (2) v(t) = 5cos(c+) t； (3) v(t) = (5 + 3cost) cosct。 解：(1) 双边带调制信号(a)；(2) 单边带调制信号(b)；(3) 普通调幅信号(c)。 4-6 何谓过调幅？为何双边带调制信号和单边带调制信号均不会产生过调幅？ 答：调制信号振幅大于载波信号振幅的情况称为过调幅。因为双边带和单边带调制信号 已经将载波信号抑制，故均不会产生过调幅。 4-8 一非线性器件的伏安特性为      = 0 0 D 0 v g v v i 式中 v = VQ 十 v1＋ v2 = VQ＋V1mcos1t＋V2mcos2t。若 V2m很小，满足线性时变条件，则在 VQ ＝ −V1m/2、0、V1m三种情况下，画出 g(v1)波形，并求出时变增量电导 g(v1)的表示式，分 析该器件在什么条件下能实现振幅调制、解调和混频等频谱搬移功能。 解：根据伏安特性画出增量电导随 v 的变化特性 g(v)如图所示

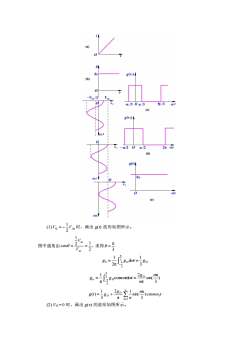
(a)glgng(m)(b)0Vim/20一元/30元/35元/3ot(c)g(v)/一元/20元/22元01(d)g(t)gpot!10VOor(e)otVm时，画出g()波形如图所示。(1)Vα =-LVm2“求得0=图中通角由cos=3V.1 Jigpdot=go=802元／斤3/Jigpcosnadar = 2e in(m)g.=2nT2g0！sin(m)g(t)=)cosno,t58+3元nEin(2)VQ=0时，画出g(v)的波形如图所示

(1) Q 1m 2 1 V = − V 时，画出 g(t) 波形如图所示。 图中通角由 ， 2 2 1 1 cos m m = = V V  求得 3 π  = D 3 π 3 0 π D 3 1 d 2π 1 g = g t = g  −  ) 3 π sin( π 2 cos d π 1 3 D π 3 n π D n n g g = g n t t =  −   n t n n g g t g n 1 1 D D ) cos 3 π sin( 1 π 2 3 1 ( )    = = + (2) VQ = 0 时，画出 g(v) 的波形如图所示

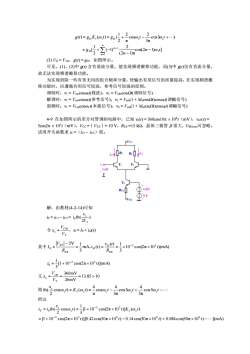
1.22g(0)=g,K,(0,t)=gp(=coso,t-cos3o,t+...)2元3元21+(-1)*-cos(2n-1)@,t)=gD[,(2n -1)元2n=l(3)Vo=V1m，g(t)=gD，如图所示。可见，（1)、(2)中g(0)含有基波分量，能实现频谱搬移功能，而(3)中g(1)仅有直流分量，故无法实现频谱搬移功能。为实现消除一些有害无用的组合频率分量，使输出有用信号的质量提高，在实现频谱搬移功能时，应遵循有用信号较弱，参考信号较强的原则。调制时：Vi=Vemcos((载波)，v2=Vomcos2(调制信号)解调时：V1=VcmcoS(（参考信号），V2=Vsm(1+Macos2t)coSt（调幅信号）混频时：Vi=VLmcoSOL（本振信号），2=Vsm(1+M.cos2t)coSO（调幅信号）4-9在如图所示的差分对管调制电路中，已知ve(l)=360cos10元×10%t（mV)，Vo(0)=5cos2元×10°t（mV），Vcc=|VEE|=10V，REE=15kQ，晶体三极管β很大，VBE(on)可忽略。试用开关函数求ic=（icl-ic2）值。Va2Rc11v(n)1解：由教材(4-2-14)可知ic= ici- ic= igth("2VTVeM, io=lo+ id)X=VT[VeE|-5VmA,1a(0)-1×10-cos2元×10°)(mA)其中I。3REEREE33[1+10-3cos(2元×10°t)](mA)10Vem:360mV=13.85>10又x。V.26mV444则 th(= cos0.1) ~ K;(@.1)= 4cos3o.t +cos5o.t--coso.t23元5元元所以ie =igth( coso.)~号=[1+10-3c0s(2元×10*1)]K(0t)2=[1+10-cos(2元×10*t)][0.42cos(10元×10°1)0.14c0s(30元×10)+0.084cos(50元×10t)-*.](mA)

cos(2 1) ] (2 1)π 2 ( 1) 2 1 [ cos3 ) 3π 2 cos π 2 2 1 ( ) ( ) ( 1 1 1 D D 1 1 D 1 1 n t n g g t g K t g t t n n     − − = + − = = + − +      = − (3) VQ = V1m，g(t) = gD，如图所示。 可见，(1)、(2)中 g(t) 含有基波分量，能实现频谱搬移功能，而(3)中 g(t)仅有直流分量， 故无法实现频谱搬移功能。 为实现消除一些有害无用的组合频率分量，使输出有用信号的质量提高，在实现频谱搬 移功能时，应遵循有用信号较弱，参考信号较强的原则。 调制时：v1 = Vcmcosct(载波)，v2 = Vmcost(调制信号) 解调时：v1 = Vcmcosct(参考信号)，v2 = Vsm(1 + Macost)cosct(调幅信号) 混频时：v1 = VLmcosLt(本振信号)，v2 = Vsm(1 + Macost)cosct(调幅信号) 4-9 在如图所示的差分对管调制电路中，已知 vc(t) = 360cos10  106 t（mV），v (t) = 5cos2  103 t（mV），VCC =｜VEE｜= 10 V，REE =15 k，晶体三极管  很大，VBE(on)可忽略。 试用开关函数求 iC =（iC1 − iC2）值。 解：由教材(4-2-14)可知 iC = iC1 − iC2 = ) 2 th( T c 0 V v i 令 ， T CM c V V x = i0 = I0 + i(t) 其中 10 cos(2π 10 )(mA) 3 ( ) 1 mA ( ) 3 5V 1 3 3 E E E E E E 0 t R v t i t R V I Ω = Ω  =   −  ， − [1 10 cos(2π 10 )](mA) 3 1 3 3 0 i = +  t − 又 13.85 10 26mV 360mV T cm c = = =  V V x 则 t  K t = t − t + t −    x c 2 c c c c c cos5 5π 4 cos3 3π 4 cos π 4 cos ) ( ) 2 th(      所以 [1 10 cos(2π 10 )][0.42 cos(10π 10 ) 0.14 cos(30π 10 ) 0.084 cos(50π 10 ) ] (mA) [1 10 cos(2π 10 ) ] ( ) 3 1 cos ) 2 th( 3 3 6 6 6 2 c 3 3 c c C 0 = +   −  +  −    =  +  − − t t t t t t K t x i i  

4-11一双差分对平衡调制器如图所示，其单端输出电流=号+22试分析为实现下列功能（不失真），两输人端各自应加什么信号电压？输出端电流包含哪些频率分量，输出滤波器的要求是什么？（1）混频（取の=oL一0c）；（2）双边带调制：（3）双边带调制波解调。VccReR教O1no(t)1aV2(0)lOVEE解：（1)混频：V(0)=vL()=VLmcOS(OLt，V2(0)=vs(t)=VsmCOS(ut，当VLm>260mV，Vsm2F的带通滤波器。(3)双边带调制波解调：vi(t)=w(t)=Vmcosaut，v2(1)=vs(t)=Vmocos2tcosOt。开关工作时，产生的组合频率分量有2，20土2，40土2，…，2n0土2。输出采用低通滤波器，BWo.7>2F。4-16采用双平衡混频组件作为振幅调制器，如图所示。图中v(t)=Vemcosot，vdl)=Vamcos.2t。各二极管正向导通电阻为RD，且工作在受vc(U)控制的开关状态。设RL>>Rp，试求输出电压 vo(0)表达式。解：作混频器，且vc>>vQ，各二极管均工作在受vc控制的开关状态。当vc>0，D1、D2导通，D3、D4截止当Vc0时，等效电路，i=ii-i2回路方程为：①Jvo -Vc +i,Rp +(ij -i2)R, =0?-②[-Vo-i,R+i2Rp-Ve=02(ii- i2)RL + 2 vo+(i1- i2)RD= 02vgi,=i-i2=-2R, +R,考虑vc作为开关函数Ki(ol)

4-11 一双差分对平衡调制器如图所示，其单端输出电流 kT qv R I v kT I i i qv i 2 th 2 2 th 2 2 1 E 0 5 6 1 0 2 I  + − = + 试分析为实现下列功能（不失真），两输人端各自应加什么信号电压？输出端电流包含哪些 频率分量，输出滤波器的要求是什么？ （1）混频（取I =L − C）；（2）双边带调制；（3）双边带调制波解调。 解：(1) 混频：v1(t) = vL(t) =VLmcosLt，v2(t) = vS(t) = Vsmcosct，当 VLm > 260 mV，Vsm 2F 的带通滤波器。 (3) 双边带调制波解调：v1(t) = vr(t) = Vrmcosct，v2(t) = vS(t) = Vm0cost cosct。开关工 作时，产生的组合频率分量有，2c  ，4c  ，，2nc  。输出采用低通滤波器， BW0.7 > 2F。 4-16 采用双平衡混频组件作为振幅调制器，如图所示。图中 vc(t) = Vcmcosct，v(t) = Vmcost。各二极管正向导通电阻为 RD，且工作在受 vC(t)控制的开关状态。设 RL>>RD，试 求输出电压 vO(t)表达式。 解：作混频器，且 vC >> v，各二极管均工作在受 vC控制的开关状态。 当 vC > 0，D1、D2 导通，D3、D4 截止 当 vC 0 时，等效电路，iI = i1 − i2 回路方程为：    − − + − = − + + − = ② ① 0 ( ) 0 I L 2 D C C 1 D 1 2 L v i R i R v v v i R i i R Ω Ω ○1 − ○2 2( i1 − i2)RL + 2 v + ( i1 − i2)RD = 0 L D I 1 2 2 2 R R v i i i Ω + = − = − 考虑 vC作为开关函数 K1(ct)

2vg()K,(0l)所以=-2R+RD(2)同理可求 vc>RD2R:. Vo(t)=-Vg(0)K(0.t)=-V(0)K2(00)2R, +Rp4-23晶体三极管混频器的输出中频频率为f=200kHz，本振频率为f=500kHz，输人信号频率为fc=300kHz。晶体三极管的静态转移特性在静态偏置电压上的幂级数展开式为ic=lo十aVbe十bvz.十Cvbc。设还有一干扰信号VM=VMmCos（2元×3.5×1051），作用于混频器的输人端。试问：（1）干扰信号vM通过什么寄生通道变成混频器输出端的中频电压？（2）若转移特性为i=lo+avbe+bve+cvbe+dvbe，求其中交叉调制失真的振幅。（3）若改用场效应管，器件工作在平方律特性的范围内，试分析干扰信号的影响。解：(1),m=350kHz，J=300kHz，由J。=%/M-得知，=1,q=2时，2/Mm-2%p"p=300kHz，表明频率为fM的干扰信号可在混频器输出，它由静态转移特性三次方项中3cVL%项产生。(2）静态特性四次方项dvb=d(ys+V+Vm）4中产生6d(vs+V）分量，而-16d(s+)=6d(+2s+)VMm1+cos20ml）中分量6VsLVMm产生中频0分2量，其幅值为3dVsmVLmVMm，包含了干扰信号包络变化造成的交叉失真。（3)由于干扰频率只能通过器件特性的三次方以上项才能产生中频频率，所以工作在平方律特性曲线内，无干扰信号的影响。4-24混频器中晶体三极管在静态工作点上展开的转移特性由下列幂级数表示：ic=lo+avbe十bvbe+cybe+dvbe。已知混频器的本振频率为f=23MHz，中频频率fi=f-f=3MHz。若在混频器输人端同时作用FMi=19.6MHz和fM2=19.2MHz的干扰信号。试问在混频器输出端是否会有中频信号输出？它是通过转移特性的几次项产生的？解：组合频率分量通式fp,s=+pft±qf。±fm±M2|中，当p=1，=0，r=2，s=1时，Jp.9Fs=fL-(2fM-fMz）=3MHz，产生中频信号输出。可见它是由转移特性四次方项vb=4(vL+VM+VM）*中12vLVMM2分量产生的，被称为互调失真，其振幅为dVLmMmMm2.24-27如图所示为发送两路语言信号的单边带发射机，试画出（A～F）各点的频谱图，图中，频率合成器提供各载波频率信号。解：A~F各点频谱图如图所示

所以 ( ) 2 2 ( ) 1 c L D I K t R R v t i Ω  + = − (2) 同理可求 vC > RD ∴ ( ) ( ) ( ) ( ) 2 2 ( ) 2 c 2 c L D L O v t K t v t K t R R R v t Ω   − Ω  + = − 4-23 晶体三极管混频器的输出中频频率为 fI = 200 kHz，本振频率为 fL = 500 kHz，输人 信号频率为 fc = 300 kHz。晶体三极管的静态转移特性在静态偏置电压上的幂级数展开式为 iC = I0＋avbe＋ 2 bvbe ＋ 3 be cv 。设还有一干扰信号 vM＝VMmcos（2×3.5×105 t），作用于混频器 的输人端。试问：（1）干扰信号 vM通过什么寄生通道变成混频器输出端的中频电压？（2） 若转移特性为 ic＝I0＋avbe＋ 2 bvbe ＋ 3 be cv + 4 dvbe ，求其中交叉调制失真的振幅。（3）若改用场 效应管，器件工作在平方律特性的范围内，试分析干扰信号的影响。 解：(1) fM = 350 kHz，fc = 300 kHz，由 c M I 1 f p p f p q f  = − 得知，p = 1，q = 2 时，2fM − 2f2 = 300 kHz，表明频率为 fM的干扰信号可在混频器输出，它由静态转移特性三次方项中 2 3cvL vM 项产生。 (2) 静态特性四次方项 4 S L M 4 be dv = d(v + v + v ) 中产生 2 M 2 S L 6d(v + v ) v 分量，而 (1 cos2 ) 2 1 6 ( ) 6 ( 2 ) M 2 Mm 2 S L L 2 S 2 M 2 S L d v + v v = d v + v v + v V +  t 中分量 2 6 S LVMm v v 产生中频 I 分 量，其幅值为 2 3dVsmVLmVMm ，包含了干扰信号包络变化造成的交叉失真。 (3)由于干扰频率只能通过器件特性的三次方以上项才能产生中频频率，所以工作在平 方律特性曲线内，无干扰信号的影响。 4-24 混频器中晶体三极管在静态工作点上展开的转移特性由下列幂级数表示：iC = I0＋ avbe＋ 2 bvbe ＋ 3 be cv + 4 dvbe 。已知混频器的本振频率为 fL = 23 MHz，中频频率 fI = fL − fc = 3 MHz。 若在混频器输人端同时作用 fM1 = 19.6 MHz 和 fM2＝19.2 MHz 的干扰信号。试问在混频器输 出端是否会有中频信号输出？它是通过转移特性的几次项产生的？ 解：组合频率分量通式 p ,q ,r,s L c M1 M2 f =  pf  qf  rf  sf 中，当 p = 1，q = 0，r = 2，s = 1 时， f p,q,r,s = f L − (2 f M1 − f M2 ) = 3MHz， 产生中频信号输出。可见它是由转移特性四次方 项 4 L M1 M2 4 be v = 4(v + v + v ) 中 M2 2 12 L M1 v v v 分量产生的，被称为互调失真，其振幅为 Mm2 2 L m Mm1 2 1 dV V V 。 4-27 如图所示为发送两路语言信号的单边带发射机，试画出（A～F）各点的频谱图， 图中，频率合成器提供各载波频率信号。 解：A~F 各点频谱图如图所示

97kHz99.7kHz100.3kHz103kHz253kHz453kHz353kHz100kHzQ97kHz99.7kHz100.3kHz103kHz253kHz100kHzC97kHz99.7kHz100.3kHz103kHz1500~3000kHz100kHz图NP4-27(S）单边带两路信号频谱图4-30包络检波电路如图所示，二极管正向电阻Rp=1002，F=（100～5000）Hz。图（a）中，Mamax=0.8；图（b）中Ma=0.3。试求图（a）中电路不产生负峰切割失真和情性失真的C和Ri2值。图（b）中当可变电阻R2的接触点在中心位置时，是否会产生负峰切割失真？解：（1)图(a)中，已知RL=RLi+RL2=5kQ，2max=2元×5000rad/s，Mamax=0.8，根据不产生情性失真条件，得V- MiC≤=4775pFR,Omex Mamax(2)根据不产生负峰切割失真条件得ZL(2) ≥ MZL(0) = MamaxRL= 4 kQ因为ZL(2)=RL1+RL2//Ri2,Mmx=0.8()R+Rts/R2_1+4/ R2R, >12kQZ, (0)5RLI + RL2(3)RL在中间位置时2(0)=R +学 / ,=1150, Z()=R +4R2=2860Q22所以至()=0.42>0.3故不产生负峰切割失真。Z, (0)

4-30 包络检波电路如图所示，二极管正向电阻 RD = 100 ，F =（100 ~ 5000）Hz。图 （a）中，Mamax = 0.8；图（b）中 Ma = 0.3。试求图（a）中电路不产生负峰切割失真和惰性 失真的 C 和 Ri2 值。图（b）中当可变电阻 R2 的接触点在中心位置时，是否会产生负峰切割 失真？ 解：(1) 图(a)中，已知 RL = RL1 + RL2 = 5 k，max = 2  5000 rad/s，Mamax = 0.8，根据 不产生惰性失真条件，得 4775pF 1 L max a max 2 a max = −  R Ω M M C (2) 根据不产生负峰切割失真条件得 ZL()  MaZL(0) = MamaxRL = 4 k 因为 ZL() = RL1 + RL2 // Ri2， Mamax = 0.8 < 12kΩ 5 // 1 4 // (0) ( ) i2 i2 L1 L2 L1 L2 i2 L L  + = + + = R R R R R R R Z Z Ω ， (3) RL 在中间位置时 // 1211.5Ω 2 ( ) i 2 L = 1 + R = R Z Ω R ， 2860Ω 2 (0) 2 L = 1 + = R Z R 所以 0.42 0.3 (0) ( ) L L =  Z Z Ω 故不产生负峰切割失真